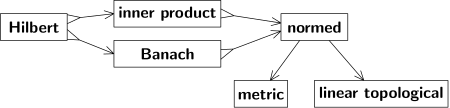
Norms, metrics, topology
Topological space
[edit | edit source]A topological space is the fundamental subject of the subdiscipline topology of mathematics. By introducing a topological structure on a set, it is possible to establish.
- intuitive positional relations like "proximity" and
- "convergence against" from the real numbers or from the , respectively.
to many and very general structures (such as the topology of function spaces).
Definition: topology
[edit | edit source]A topology is a set system consisting of subsets (open sets) of a basic set for which the following axioms are satisfied.
- (T1)
- (T2) for all .
- (T3) For any index set and for all holds: .
A set together with a topology on is called topological space .
Remark - closed sets
[edit | edit source]By defining all open sets in by the topology , all closed sets are also defined as complements of an open set .
Definition - open kernel of a set
[edit | edit source]Let be in the topological space , then the open core is defined as the "largest" open set contained in :
Remark - open core
[edit | edit source]Since in the definition is represented as the union of open sets , open by axiom (T3).
Definition - connection of a set
[edit | edit source]Let be in the topological space , then the closure is defined as the "smallest" closed set containing :
Remark - open core
[edit | edit source]Since in the definition is represented as the intersection of closed sets with , is again open as the completion of any union of open sets, since it holds again according to (T3):
Definition - Boundary of a set
[edit | edit source]Let be a set in the topological space , then the edge of a set from the closure of the set without the open core of . The boundary is therefore defined as follows:
- .
Remark
[edit | edit source]The sets are by definition open and mutually the two sets form the complements of each other. Thus these two sets are both open and closed at the same time. Therefore, the two sets have no boundary points.
Definition - Neighbourhood
[edit | edit source]Let and be a set in a topological space , then the is called Neighbourhood of if there exists an open set with:
The set of all Neighbourhood of with respect to the topology is denoted by . denotes the set of all open neighbourhoods of .
Definition - Neighbourhood basis
[edit | edit source]Let and a set system in a topological space , then the \mathcal{B} is called the neighbourhood basis of if the following properties hold:
- (B1)
- (B2) for each environment a neighborhood with .
Example
[edit | edit source]The set of open neighbourhood in with the Euclidean topology generated by the amount is an neighbourhood basis of .
Remark
[edit | edit source]The neighbourhood basis term helps to prove convergence statements for the neighbourhood basis only, and thus to obtain the statements for arbitrary neighbourhoods as well. In calculus one uses -neighbourhoods in definitions without explicitly addressing the topological aspect of the neighbourhood basis, that proofs in general arbitrary neighbourhoods and not only for the neighbourhood basis. Due to the fact that an arbitrary neighbourhood contains a set of the neighbourhood basis, the most of the convergence proofs can limit themselves to the neighbourhood basis.
Definition - base of topology
[edit | edit source]Let and be a set system in a topological space , then the is called the basis of if holds:
- (BT1)
- (BT2) for every open set there is an open set with .
Example
[edit | edit source]The set of all open intervals is a basis of the topology in the topological with the Euclidean topology generated by the amount .
Convergence in topological spaces
[edit | edit source]In calculus, the convergence of sequences is a central definition to define notions based on it, such as continuity, difference, and integrals. Sequences with as index set are unsuitable to define convergence in general topological spaces, because the index set is not powerful enough concerning the neighbourhood basis. This is only possible if the topological space has a countable neighbourhood basis. Therefore one goes over either to nets or Filters
Example: topology on texts
[edit | edit source]Usually, one assumes that topologies are defined on mathematical spaces (e.g., number spaces, function spaces, (topological) groups, vector spaces, ...). However, the generality of the definition makes it also possible to define a topology on texts. This example was added because purely descriptively, e.g., texts in the German language
- can have a similar statement and
- use different words.
This similarity of semantics, or syntax, is explored in more detail as an exercise in "Topology on Texts".
Describe similarity of words by metrics
[edit | edit source]From spoken words, represent the number of letters and the set of occurring letters as a table. How can you derive a distance of words from the tabulated list. make a suggestion for this. What are the properties of your proposed distance function. Is it a metric on the space of words?
Task - distance between words
[edit | edit source]- Consider the words "bucket", "buket", "buckett". How can you express the differences of the words by a metric
- Phonetic similarity words "bucket" and "pucket" have a phonetic similarity, but from the sequence of letters the spellings differ greatly. How can you notate similarity of spoken words (Speech Recognition) by a phonetic notation and in this notation of phonemes express a similarity of words as well.
Classification of topological spaces
[edit | edit source]Meaning of Properties topology
[edit | edit source]- (T1) empty set and the basic set are open sets.
- (T2) for all : the average of finitely many open sets is an open set.
- (T3) The union of any many open sets is again an open set.
Semantics: metric
[edit | edit source]A metric associates with two elements from a base space the distance between and .
Definition: Metric
[edit | edit source]Let be an arbitrary set. A mapping is called a metric on if for any elements , and of the following axioms are satisfied:
- (M1) separation: ,
- (M2) symmetry: ,
- (M3) triangle inequality: .
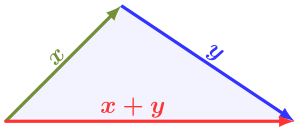
Illustration: metric triangle inequality
[edit | edit source]According to the triangle inequality, the distance between two points X,Y is at most as large as sum of the distances from X to Z and from Z to Y, that is, a detour via the point Z
Non-negativity
[edit | edit source]Non-negativity follows from the three properties of the metric, i.e. for all holds. . The non-negativity follows from the other properties with:
- .
Open sets in metric spaces
[edit | edit source]- In a metric space , one defines a set to be open (i.e. ) if for every there is a that the -sphere lies entirely in (i.e. i.e. )
- Show that with this defined , the pair is a topological space (i.e., (T1), (T2), (T3) satisfied).
Norm on vector spaces
[edit | edit source]A norm is a mapping from a vector space over the body of the real or the complex numbers into the set of nonnegative real numbers . Here the norm assigns to each vector its length .
Definition: Norm
[edit | edit source]Let be a vector space and a mapping. If satisfies the following axioms axioms N1,N2, N3, then is called a norm on .
- (N1) Definiteness: for all ,
- (N2) absolute homogeneity: for all and .
- (N3) Triangle inequality: for all .
Remark: N1
[edit | edit source]The property (N1) is actually an equivalence and it holds in any normed space. If is the zero vector in and is the zero in the field , if is a vector space).
- (N1)' definiteness: for all ,
- Since one uses a minimality principle for definitions for the defining property, one would not use a stronger formulation (N1)' in the definition for (N1), since the equivalence from the defining properties of the norm follow the properties of the vector space already for any normed space.
Normed space / Metric space
[edit | edit source]A normed space is also a metric space.
- A norm assigns to a vector its vector length .
- The norm can be used to define a metric via that specifies the distance between and .
Learning Task: generate metric from given norm
[edit | edit source]Let be a normed space with norm . Show that the defined mapping with satisfies the properties of a metric.
Notation: norm
[edit | edit source]- In the axiom (N2) , denotes the amount of the scalar. "" sign: Outer linkage in vector space or multiplication .
- indicates the length of the vector .
- In (N3) for all . '""-sign denotes two distinct links (i.e., addition in and , respectively.
Illustration: norm triangle inequality
[edit | edit source]Def: convergence in normalized space
[edit | edit source]Let be a normalized space and a sequence in and :
Def: convergence in metric space
[edit | edit source]Let be a metric space and a sequence in and :
Def: Cauchy sequences in metric spaces
[edit | edit source]Let be a metric space and a sequence in . is called a Cauchy sequence in :
Equivalence: norms
[edit | edit source]Let two norms and be given on the vector space . The two norms are equivalent if holds:
- .
Show that a sequence converges in exactly if it also converges with respect to .
Absolute value in complex numbers
[edit | edit source]Let be a complex number with . Show that is a norm on the vector space !
Historical Notes: Norm
[edit | edit source]This axiomatic definition of norm was established by Stefan Banach in his 1922 dissertation. The norm symbol in use today was first used by Erhard Schmidt in 1908 as the distance between vectors and .
See also
[edit | edit source]- Absolute value
- Complex Analysis
- Inverse-producing extensions of Topological Algebras
- Functional analysis
Page Information
[edit | edit source]You can display this page as Wiki2Reveal slides
Wiki2Reveal
[edit | edit source]The Wiki2Reveal slides were created for the Functional analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.
- This page is designed as a PanDocElectron-SLIDE document type.
- Source: Wikiversity https://en.wikiversity.org/wiki/Norms,%20metrics,%20topology
- see Wiki2Reveal for the functionality of Wiki2Reveal.