MyOpenMath/Electromagnetic momentum

• 
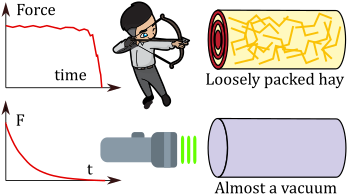
  Electromagnetic momentum archery analogy
• 
  Click to expand
• 
  Current element

${\text{Impulse}}=\int F(t)dt\rightarrow {\mathcal {P}}{\text{ (momentum)}}$

(1)

Fundamental equations

$B=B_{x}$ magnetic field	$J=J_{y}=\sigma E_{y}$ current density	$f=f_{x}=J_{y}B_{z}=\sigma EB$ force density
$\alpha ={\frac {\sigma }{2\varepsilon _{0}}}$ damping rate	$c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}$ light speed	$S=S_{x}={\frac {1}{\mu _{0}}}E_{y}B_{z}$ Poynting vector
${\frac {\partial ^{2}E}{\partial t^{2}}}+2\alpha {\frac {\partial E}{\partial t}}-c^{2}{\frac {\partial ^{2}E}{\partial x^{2}}}=0$ wave equation		${\frac {\partial B}{\partial t}}=-{\frac {\partial E}{\partial x}}$ Faraday's law

The force density $f$ is the force per unit volume. Because this transverse electromagnetic wave causes no charge density to form, the only force is magnetic and caused by currents,

$d{\vec {F}}=Id{\vec {\ell }}\times {\vec {B}}={\vec {J}}\times {\vec {B}}\,dV_{\text{ol}}$,

(2 ImpMom)

where $dV_{\text{ol}}$ is the volume of the current element. This force does not occur in a vacuum (i.e., when $\sigma =0$) because no current can flow without matter present. The Poynting vector is the rate at which energy flows through an area:

${\vec {S}}={\frac {{\vec {E}}\times {\vec {B}}}{\mu _{0}}}=\varepsilon _{0}c^{2}{\vec {E}}\times {\vec {B}}={\frac {\text{power}}{\text{area}}}$

(3 poy)

The fact that all the coefficients in the wave equation are real permits us to work almost exclusively with complex solutions, taking the real part only at the end. To facilitate matters, all complex numbers will be marked with a tilde ($\sim$). In this discussion we stipulate that wavenumber, $k$, be real. Here, the real part of the complex angular frequency ${\widetilde {\omega }}$, has no tilde: $\omega =\Re e({\widetilde {\omega }})$. It is far more customary to model radiation in a conducting medium with a real-valued frequency, with a complex wavenumber to model the skin effect. This unorthodox approach is motivated by the fact that formulas for the damped harmonic oscillator have already been introduced in an OpenStax textbook. The relation between ${\widetilde {\omega }}$ and $k$ is can also be solved for linear differential equations with constant coefficients using an interesting fact: Derivatives and integrals are often reduced to a matter of simple multiplication. For example:

${\begin{aligned}\partial /\partial x&=ik\\\partial /\partial t&=-i{\widetilde {\omega }}\end{aligned}}\,{\Big \}}$ when operating on $\,e^{i(kx-{\widetilde {\omega }}t)}$.

(4 DifOps)

The two entries in the table labeled wave equation and Faraday's law are partial differential equations that are suitable for application of (4 DifOps). The former leads to what is known as a dispersion relation:

${\widetilde {\omega }}^{2}+2i\alpha {\widetilde {\omega }}-c^{2}k^{2}=0.$

(5 dspRln)

The real and imaginary parts of ${\widetilde {\omega }}$ are:

${\begin{aligned}{\widetilde {\omega }}=&\omega -i\alpha \\\omega =&{\mathcal {Re}}({\widetilde {\omega }})={\sqrt {k^{2}c^{2}-\alpha ^{2}}}\\\alpha =&{\mathcal {Im}}({\widetilde {\omega }})=\sigma /2\varepsilon _{0}.\end{aligned}}$

(6 ReImW)

Too many variables, dimensions, and equations

Each unnecessary variable in a system of equations adds an extra equation required to define it. Expressing quantities in just a few dimensions – and awareness of those dimensions – will help you avoid making the mistake of omitting variables from an equation. Inspection of (4-6) uncovers the fact that many of our variables involve time: $[{\widetilde {\omega }}^{2}]=[i\alpha {\widetilde {\omega }}]=[c^{2}k^{2}]={\mathsf {T^{-2}}}$. For that reason, whenever possible, it is better to avoid conductivity $\sigma$, by instead using the damping rate $\alpha =\sigma /2\varepsilon _{0}$. This also reminds you that the wave is damped because $\sigma$ is not zero.

Most calculations in this textbook are based on three of the seven so-called "fundamental units": (length, mass, time)$={\mathsf {(L,M,T)}}$. Given the role force plays in (1), we are at liberty to treat, ${\mathsf {F}}={\mathsf {M}}{\mathsf {L}}{\mathsf {T}}^{-2}$, as a basic unit. The Poynting vector plays is defined as rate at which energy passes through a unit area, and is introduced in most textbooks. The unit of energy is the joule, which equals one newton-meter. This renders the dimensions of the Poynting vector easy to write: $[S]={\mathsf {F/TL}}$. Force density is now easily expressed in terms the Poynting vector:

$f=|{\vec {J}}\times {\vec {B}}|=\sigma EB=\overbrace {\left(2\alpha \right)} ^{\sigma /\varepsilon _{0}}\cdot \overbrace {\left(1/c^{2}\right)} ^{\varepsilon _{0}\mu _{0}}\cdot \overbrace {(\;S\;)} ^{EB/\mu _{0}}={\frac {2\alpha }{c^{2}}}S$.

(7 frcDen)

The Poynting vector was previously introduced as the rate at which electromagnetic energy flows Since the joule is one newton-meter, we can also write the force density in terms of the Poynting vector:

Oscillating magnetic field

The complex function representing the electric field is given at (E-field), where take $E_{0}$ to be a real number. From the table we use Faraday's law to obtain the magnetic field, using the "trick" at (4 DifOps) to convert differential operations into multiplication by complex numbers.

${\widetilde {B}}(x,t)={\frac {k}{\widetilde {\omega }}}E_{0}e^{i(kx-{\widetilde {\omega }}t)}={\frac {k(\omega +i\alpha )}{k^{2}c^{2}+\alpha ^{2}}}E_{0}e^{-\alpha t}e^{i(kx-\omega t)}$

(8 Btild)

In the second step above we multiplied the numerator and denominator by the complex conjugate, ${\widetilde {\omega }}^{*}=\omega -i\alpha$. Comparison with (Efield) suggests that we define an analog to the amplitude of the electric field, $E_{0}$. To remind ourselves that this magnetic field amplitude is complex, we place a tilde above it:

${\widetilde {B}}_{0}={\frac {k}{\widetilde {\omega }}}E_{0}={\frac {k(\omega +i\alpha )}{k^{2}c^{2}+\alpha ^{2}}}E_{0}$

(9 BoTil)

First, we we replace (8 BoTil) by the following approximation, valid for very small $\alpha$. In the limit that $\alpha \rightarrow 0$ we may write:

${\widetilde {B}}_{0}={\frac {1}{c}}E_{0}e^{-\alpha t}\underbrace {\;+\;...\approx {\frac {1}{c}}E_{0}e^{-\alpha t}} _{\text{notation}}=B_{0}$

(10 Bo)

The parts of this equation labeled as "notation" have no meaning in a first reading of this essay. But after a year of physics and a two years of calculus it will become necessary to look more closely at limits and approximations like this. And finally, in (Bo) we removed the tilde on $B_{0}$ because in this approximation ${\widetilde {B}}_{0}$ is real valued.

Introduction to phasors

Equation (6 frcDen) relates the force density, $f=2\alpha S/c^{2}$ to Poynting vector, which is also the product of two oscillating fields. Equation (1) suggests that we integrate this product. But the product of two complex waves proportional to $\exp(i(kx-{\widetilde {\omega }}t))$ is does not permit the use of (4 DifOps) to avoid the calculus of integration and differentiation. This can be resolved using phasors, which some physicists regard simply as the use of complex numbers to solve a problem originally posed in terms of purely real number.

Here, we follow the discussion at MyOpenMath/Complex phasors average out the high frequency $\omega$ oscillations. We shall not concern ourselves whether the results are exact, or simply approximate in the limit that the exponential decay a the rate $\alpha$ is much slower than the sinusoidal oscillation rate, i.e. in the limit that,

${\frac {\alpha }{\omega }}<<1$

(11 aprx)

We also use the approximation from (9 Bo) that ${\widetilde {B}}_{0}$ is real, and denote this time average with the overline ${\overline {EB}}$. Details of the algebra leading to the following equation can be found at Phasor algebra.

${\overline {EB}}=\Re e{\frac {{\widetilde {E}}{\widetilde {B}}^{*}}{2}}=$${\tfrac {E_{0}}{\sqrt {2}}}e^{-\alpha t}\underbrace {e^{i(kx-\omega t+\phi _{E})}} _{\text{cancel}}{\tfrac {B_{0}^{*}}{\sqrt {2}}}e^{-\alpha t}\underbrace {e^{-i(kx-\omega t+\phi _{B})}} _{\text{cancel}}$$=E_{\text{rms}}B_{\text{rms}}\cos(\Delta \phi )$,

(12 cancl)

where $\Delta \phi =\phi _{E}-\phi _{B}$ is the difference in phase shift between the two signals. The root-mean-square is, for example,

$E_{\text{rms}}={\sqrt {\;{\overline {\;(E_{0}\cos \omega t)^{2}\;}}\;}}={\tfrac {1}{\sqrt {2}}}E_{0}$.

(13 rms)

Equation (11 cancel) is easy to remember because it matches the case for dc signals where the phase shift, $\phi _{E}-\phi _{B}$, always vanishes. This phase shift always vanishes in (11) because the approximation (9 Bo) was made. Another reason (11 cancel) easy to remember is that it does not matter which variable is converted to its complex conjugate (*), since $\Re e\left({\widetilde {E}}{\widetilde {B}}^{*}\right)=\Re e\left({\widetilde {E}}^{*}{\widetilde {B}}\right)$. Finally, it is easy to remember the rms of $\cos \omega t$, due to the identity, $\sin ^{2}\omega t+\cos ^{2}\omega t=1$, combined with the fact that both sinusoidal functions will have the same rms average values (provided a proper time interval is used.)

Under construction

Converting force density $f$ to force requires a volume integral, and integration of (1) using (6frcDen) gives us the amount of momentum ${\mathcal {P}}$ a wavepacket will transfer to the slightly conducting medium:

${\mathcal {P}}=\int dV_{\text{ol}}\int _{0}^{\infty }f({\vec {r}},t)dt=\int dV_{\text{ol}}\;{\frac {2\alpha }{c^{2}}}S({\vec {r}})\underbrace {\int _{0}^{\infty }e^{-2\alpha t}\;dt} _{1/2\alpha }$.

(14 PfS)

If we use curly brackets $\{\,\}$ to denote momentum density,

${\vec {\mathcal {P}}}=\int dV_{\text{ol}}\left\{{\tfrac {1}{c^{2}}}{\vec {S}}\right\}.$

(15 Pcb)

The wavepacket's energy and energy density are represented in a similar fashion:

${\mathcal {U}}=\int dV_{\text{ol}}\left\{{\tfrac {\varepsilon _{0}}{2}}E^{2}+{\tfrac {1}{2\mu _{0}}}B^{2}\right\}$

(16 Ucb)

While (15) and (16) were derived here for the special case of light travelling in a vacuum, these expressions for momentum and energy density hold for a much broader range of conditions. For light in vacuo, $E=cB$, using formula for energy density of electromagnetic fields, we conclude:

${\mathcal {U}}=c|{\vec {\mathcal {P}}}|$

(17 U-cP)