Mechanics of materials/Problem set 4

Completion status: this resource is a stub, which means that pretty much nothing has been done yet.

Problem 4.1

P3.23, Beer 2012
On our honor, we did this problem on our own, without looking at the solutions in previous semesters or other online solutions.

Problem Statement

Under normal operating conditions a motor exerts a torque of magnitude $T_{F}$ =1200 lb*in. at F. $r_{D}$ =8in., $r_{G}$ =3in., and the allowable shearing stress is 10.5 ksi in each shaft.

Objective

Determine the required diameter of (a) shaft CDE, (b) shaft FGH.

Solution

Step 1

FBD

Step 2

We can write an equilibrium equation: The moment about the center point D.

$\sum M_{D}=0=T_{E}-F(r_{D})$

$\Rightarrow F={\frac {T_{E}}{r_{D}}}$

FBD

Step 3

We can write an equilibrium equation: The moment about the center point G.


$\sum M_{G}=0=T_{F}-F(r_{G})$

$\Rightarrow F={\frac {T_{F}}{r_{G}}}$

(a)

FBD

Step 4

Now we set the two Forces (F) equal to each other and solve.


${\frac {T_{E}}{r_{D}}}={\frac {T_{F}}{r_{G}}}\Rightarrow T_{E}={\frac {T_{F}*r_{D}}{r_{G}}}={\frac {1200lb*in*8in}{3in}}=3200lb*in$

Step 5

Solve $\tau _{max}$
$\tau _{max}={\frac {T_{E}*C_{D}}{J}}\Rightarrow C_{D}={\sqrt[{3}]{\frac {2T_{E}}{\pi \tau _{max}}}}={\sqrt[{3}]{\frac {2*3200lb*in}{\pi 10.5*10^{3}{\frac {lb}{in^{2}}}}}}=0.58in$

Step 6

Solve for the diameter of shaft CDE

$d_{D}=2*C_{D}=2*0.58in=1.158in$

(b)

Step 7

FBD

Step 8

Solve $\tau _{max}$

$\tau _{max}={\frac {T_{F}*C_{F}}{J}}\Rightarrow C_{F}={\sqrt[{3}]{\frac {2T_{F}}{\pi \tau _{max}}}}={\sqrt[{3}]{\frac {2*1200lb*in}{\pi 10.5*10^{3}{\frac {lb}{in^{2}}}}}}=0.417in$

Step 9

Solve for the diameter of shaft FGH

$d_{F}=2*C_{F}=2*0.42in=0.835in$

Problem 4.2

P3.25, Beer 2012
On our honor, we did this problem on our own, without looking at the solutions in previous semesters or other online solutions.

Problem Statement

The two solid shafts are connected by gears as shown and are made of steel for which the allowable shearing stress is 8500 psi. A torque of magnitude $T_{C}$ =5 kip*in. is applied at C and the assembly is in equilibrium.

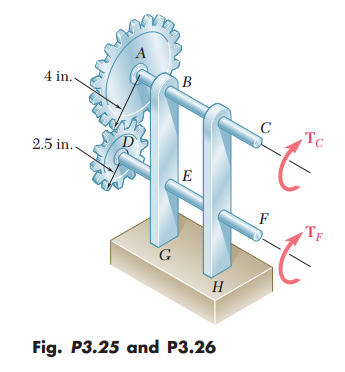
Objective

Determine the required diameter of (a) shaft BC, (b) shaft EF.

Solution

Step 1

First sum the moments around gears A and E

$\sum M_{A}=F_{A}*R_{C}+T_{C}$

$\sum M_{D}=F_{D}*R_{F}+T_{F}$

Solve for F

$F={\frac {T}{R}}$

Step 2

Sum the Forces

$\sum F=0=F_{C}+F_{F}={\frac {T_{C}}{R_{A}}}+{\frac {T_{F}}{R_{E}}}$

Step 3

Solve for $T_{F}$


$T_{F}={\frac {-T_{C}*R_{E}}{R_{A}}}={\frac {-5kipin*2.5in}{4in}}=-3.125kip*in$


The magnitude of $T_{F}$ = 3.125 kip*in

Step 4

Use the formula for $\tau _{max}$ to solve for the radius


$\tau _{max}={\frac {T*r}{J}}={\frac {2*T}{\pi *r^{3}}}$

$r^{3}={\frac {2*T}{\pi *\tau _{max}}}$

$r=({\frac {2*T}{\pi *\tau _{max}}})^{1/3}$

Step 5

Input the Given values into the equation for the radius

$d_{C}=2*r_{C}=2*({\frac {2*T_{C}}{\pi *\tau _{max}}})^{1/3}=2*({\frac {2*5000lb*in}{\pi *8500psi}})^{1/3}=1.44in$

$d_{F}=2*r_{F}=2*({\frac {2*T_{F}}{\pi *\tau _{max}}})^{1/3}=2*({\frac {2*3125lb*in}{\pi *8500psi}})^{1/3}=1.233in$