Mathematics for Applied Sciences (Osnabrück 2023-2024)/Part I/Lecture 5

Ordering properties of the real numbers

It is known that the real number may be identified with the points on a line. If on the number line, a point is further on the right than another point, then its value is larger. We describe now these ordering properties of the real numbers.

Definition

A field ${}K$ is called an ordered field, if there is a relation ${}>$ (larger than) between the elements of ${}K$, fulfilling the following properties (${}a\geq b$ means ${}a>b$ or ${}a=b$).

1. For two elements ${}a,b\in K$, we have either ${}a>b$ or ${}a=b$ or ${}b>a$.
2. From ${}a\geq b$ and ${}b\geq c$, one may deduce ${}a\geq c$ (for any ${}a,b,c\in K$).
3. ${}a\geq b$ implies ${}a+c\geq b+c$ (for any ${}a,b,c\in K$).
4. From ${}a\geq 0$ and ${}b\geq 0$, one may deduce ${}ab\geq 0$ (for any ${}a,b\in K$).

${}\mathbb {Q}$ and ${}\mathbb {R}$ are, with their natural orderings, ordered fields.

Lemma

In an ordered field, the following properties hold.

1. ${}1\geq 0$.
2. ${}a\geq 0$ holds if and only if ${}-a\leq 0$ holds.
3. ${}a\geq b$ holds if and only if ${}a-b\geq 0$ holds.
4. ${}a\geq b$ holds if and only if ${}-a\leq -b$ holds.
5. ${}a\geq b$ and ${}c\geq d$ imply ${}a+c\geq b+d$.
6. ${}a\geq b$ and ${}c\geq 0$ imply ${}ac\geq bc$.
7. ${}a\geq b$ and ${}c\leq 0$ imply ${}ac\leq bc$.
8. ${}a\geq b\geq 0$ and ${}c\geq d\geq 0$ imply ${}ac\geq bd$.
9. ${}a\geq 0$ and ${}b\leq 0$ imply ${}ab\leq 0$.
10. ${}a\leq 0$ and ${}b\leq 0$ imply ${}ab\geq 0$.

Proof

See Exercise 5.5 .

$\Box$

Lemma

In an ordered field, the following properties holds.

1. From ${}x>0$ one can deduce ${}x^{-1}>0$.
2. From ${}x<0$ one can deduce ${}x^{-1}<0$.
3. For ${}x>0$ we have ${}x\geq 1$ if and only if ${}x^{-1}\leq 1$.
4. From ${}x\geq y>0$ one can deduce ${}x^{-1}\leq y^{-1}$.
5. For positive elements ${}x,y$ the relation ${}x\geq y$ is equivalent with ${}{\frac {x}{y}}\geq 1$.

Proof

See Exercise 5.8 , Exercise 5.37 , Exercise 5.9 , Exercise 5.10 and Exercise 5.11 .

$\Box$

Definition

Let ${}K$ be an ordered field. ${}K$ is called Archimedean, if the following Archimedean axiom holds, i.e. if for every ${}x\in K$ there exists a natural number ${}n$ such that

${}n\geq x\,.$

Lemma

1. For ${}x,y\in \mathbb {R}$ with ${}x>0$ there exists ${}n\in \mathbb {N}$ such that ${}nx\geq y$.
2. For ${}x>0$ there exists a natural number ${}n$ such that ${}{\frac {1}{n}}<x$.
3. For two real numbers ${}x<y$ there exists a rational number ${}n/k$ (with ${}n\in \mathbb {Z}$, ${}k\in \mathbb {N} _{+}$) such that

   ${}x<{\frac {n}{k}}<y\,.$

Proof

(1). We consider ${}y/x$. Because of the Archimedean axiom there exists some natural number ${}n$ with ${}n\geq y/x$. Since ${}x$ is positive, due to Lemma 5.2   (6) also ${}nx\geq y$ holds. For (2) and (3) see Exercise 5.21 .

$\Box$

Definition

For real numbers ${}a,b$, ${}a\leq b$, we call

1. ${}[a,b]={\left\{x\in \mathbb {R} \mid x\geq a{\text{ and }}x\leq b\right\}}$ the closed interval.
2. ${}]a,b[={\left\{x\in \mathbb {R} \mid x>a{\text{ and }}x<b\right\}}$ the open interval.
3. ${}]a,b]={\left\{x\in \mathbb {R} \mid x>a{\text{ and }}x\leq b\right\}}$ the half-open interval (closed on the right).
4. ${}[a,b[={\left\{x\in \mathbb {R} \mid x\geq a{\text{ and }}x<b\right\}}$ the half-open interval (closed on the left).

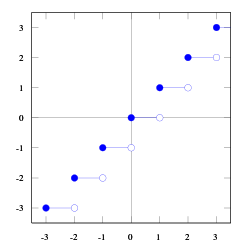
For the real numbers, the intervals with bounds from ${}\mathbb {Z}$ ${}[n,n+1[$, ${}n\in \mathbb {Z}$, form a disjoint union or a covering of ${}\mathbb {R}$. Therefore, the following definition makes sense.

Definition

For a real number ${}x$, the floor ${}\left\lfloor x\right\rfloor$ is defined as

$\left\lfloor x\right\rfloor =n,{\text{ if }}x\in [n,n+1[{\text{ and }}n\in \mathbb {Z} .$

With the ordering properties, we can also define increasing and decreasing functions.

Definition

Let ${}I\subseteq \mathbb {R}$ denote an interval and let

$f\colon I\longrightarrow \mathbb {R}$

denote a function. Then ${}f$ is called increasing if

$f(x')\geq f(x){\text{ holds for all }}x,x'\in I{\text{ with }}x'\geq x,$

strictly increasing if

$f(x')>f(x){\text{ holds for all }}x,x'\in I{\text{ with }}x'>x,$

decreasing if

$f(x')\leq f(x){\text{ holds for all }}x,x'\in I{\text{ with }}x'\geq x,$

strictly decreasing if

$f(x')<f(x){\text{ holds for all }}x,x'\in I{\text{ with }}x'>x.$

The modulus

Definition

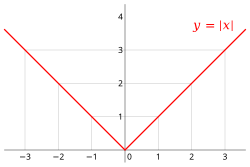
For a real number ${}x\in \mathbb {R}$, the modulus is defined in the following way.

${}\vert {x}\vert ={\begin{cases}x\,,{\text{ if }}x\geq 0\,,\\-x,\,{\text{ if }}x<0\,.\end{cases}}\,$

So the modulus (also called the absolute value) is never negative and has only at ${}x=0$ the value ${}0$, elsewhere it is always positive. The mapping

$\mathbb {R} \longrightarrow \mathbb {R} ,x\longmapsto \vert {x}\vert ,$

is called the modulus function. Its graph consists of two half lines; such a function is called piecewisely linear.

Lemma

The modulus function

$\mathbb {R} \longrightarrow \mathbb {R} ,x\longmapsto \vert {x}\vert ,$

fulfills the following properties (${}x,y$ are arbitrary real numbers).

1. ${}\vert {x}\vert \geq 0$.
2. ${}\vert {x}\vert =0$ if and only if ${}x=0$.
3. ${}\vert {x}\vert =\vert {y}\vert$ if and only if ${}x=y$ or ${}x=-y$ holds.
4. ${}\vert {y-x}\vert =\vert {x-y}\vert$.
5. ${}\vert {xy}\vert =\vert {x}\vert \vert {y}\vert$.
6. For ${}x\neq 0$ we have ${}\vert {x^{-1}}\vert =\vert {x}\vert ^{-1}$.
7. We have ${}\vert {x+y}\vert \leq \vert {x}\vert +\vert {y}\vert$ (triangle inequality for the modulus).
8. ${}\vert {x+y}\vert \geq \vert {x}\vert -\vert {y}\vert$.

Proof

See Exercise 5.23 .

$\Box$

Bernoulli's inequality

Bernoulli's inequality for ${}n=3$.

The following statement is called Bernoulli's inequality.

Theorem

For every real number ${}x\geq -1$, and a natural number ${}n$, the estimate

${}(1+x)^{n}\geq 1+nx\,$

holds.

Proof

We do induction over ${}n$.  Suppose that the statement is already known for ${}n$. Then

${}{\begin{aligned}(1+x)^{n+1}&=(1+x)^{n}(1+x)\\&\geq (1+nx)(1+x)\\&=1+(n+1)x+nx^{2}\\&\geq 1+(n+1)x,\end{aligned}}$

since squares in an ordered field are nonnegative.

$\Box$

The complex numbers

We are going to introduce the complex numbers starting from the real numbers. It is not important for this construction that we have not completely listed all properties of the real numbers so far. We will use however that every positive real number has a unique real square root. With the construction of the complex numbers, we then have all number domains which are relevant for us.

Definition

The set ${}\mathbb {R} ^{2}$ with ${}0:=(0,0)$ and ${}1:=(1,0)$, with componentwise addition and the multiplication defined by

${}(a,b)\cdot (c,d):=(ac-bd,ad+bc)\,,$

is called the field of complex numbers. We denote it by

$\mathbb {C} .$

So the addition is just the vector addition in ${}\mathbb {R} ^{2}$, but the multiplication is a new operation. We will see in Fact ***** a more geometric interpretation for the complex multiplication.

Lemma

The complex numbers form a

field.

Proof

See Exercise 5.32 .

$\Box$

From now on we write

${}a+b{\mathrm {i} }:=(a,b)\,$

and in particular we put ${}{\mathrm {i} }=(0,1)$, this number is called the imaginary unit. It has the important property

${}{\mathrm {i} }^{2}=-1\,.$

From this property and the rules of a field, one can deduce all algebraic properties of the complex numbers. This also helps in memorizing the multiplication rule as we have

${}(a+b{\mathrm {i} })(c+d{\mathrm {i} })=ac+ad{\mathrm {i} }+b{\mathrm {i} }c+b{\mathrm {i} }d{\mathrm {i} }=ac+bd{\mathrm {i} }^{2}+(ad+bc){\mathrm {i} }=ac-bd+(ad+bc){\mathrm {i} }\,.$

We consider a real number ${}a$ as the complex number ${}a+0{\mathrm {i} }=(a,0)$. Hence ${}\mathbb {R} \subset \mathbb {C}$. It does not make a difference whether we add or multiply real numbers as real numbers or as complex numbers.

Definition

For a complex number

${}z=a+b{\mathrm {i} }\,,$

we call

${}\operatorname {Re} \,{\left(z\right)}=a\,$

the real part of ${}z$ and

${}\operatorname {Im} \,{\left(z\right)}=b\,$

the imaginary part of ${}z$.

However, one should not think that complex numbers are less real than real numbers. The construction of the complex numbers starting from the reals is by far easier than the construction of the real numbers starting from the rational numbers. On the other hand, it was a long historic process until complex numbers were accepted as numbers; they form a field, but not an ordered field, and so at first glance they are numbers which do not measure anything.

One should think of complex numbers as points of the plane; for the additive structure we have directly ${}\mathbb {C} =\mathbb {R} ^{2}$. The horizontal axis is called the real axis and the vertical axis is called the imaginary axis.

Lemma

The real part and the imaginary part of complex numbers fulfill the following properties (for

${}z$ and ${}w$ in ${}\mathbb {C}$).

1. ${}z=\operatorname {Re} \,{\left(z\right)}+\operatorname {Im} \,{\left(z\right)}{\mathrm {i} }$.
2. ${}\operatorname {Re} \,{\left(z+w\right)}=\operatorname {Re} \,{\left(z\right)}+\operatorname {Re} \,{\left(w\right)}$.
3. ${}\operatorname {Im} \,{\left(z+w\right)}=\operatorname {Im} \,{\left(z\right)}+\operatorname {Im} \,{\left(w\right)}$.
4. For ${}r\in \mathbb {R}$ we have

   $\operatorname {Re} \,{\left(rz\right)}=r\operatorname {Re} \,{\left(z\right)}{\text{ and }}\operatorname {Im} \,{\left(rz\right)}=r\operatorname {Im} \,{\left(z\right)}.$

5. ${}z=\operatorname {Re} \,{\left(z\right)}$ holds if and only if ${}z\in \mathbb {R}$ holds, and this holds if and only if ${}\operatorname {Im} \,{\left(z\right)}=0$ holds.

Proof

See Exercise 5.34 .

$\Box$

Definition

The mapping

$\mathbb {C} \longrightarrow \mathbb {C} ,z=a+b{\mathrm {i} }\longmapsto {\overline {z}}:=a-b{\mathrm {i} },$

is called complex conjugation.

For ${}z$, the number ${}{\overline {z}}$ is called the complex-conjugated number of ${}z$. Geometrically, the complex conjugation to ${}z\in \mathbb {C}$ is simple the reflection at the real axis.

Lemma

For the complex conjugation, the following rules hold (for arbitrary

${}z,w\in \mathbb {C}$).

1. ${}{\overline {z+w}}={\overline {z}}+{\overline {w}}$.
2. ${}{\overline {-z}}=-{\overline {z}}$.
3. ${}{\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}}$.
4. For ${}z\neq 0$ we have ${}{\overline {1/z}}=1/{\overline {z}}$.
5. ${}{\overline {\overline {z}}}=z$.
6. We have ${}{\overline {z}}=z$ if and only if ${}z\in \mathbb {R}$ holds.

Proof

See Exercise 3.41 .

$\Box$

Lemma

For a complex number

${}z$ the following relations hold.

1. ${}{\overline {z}}=\operatorname {Re} \,{\left(z\right)}-{\mathrm {i} }\operatorname {Im} \,{\left(z\right)}$.
2. ${}\operatorname {Re} \,{\left(z\right)}={\frac {z+{\overline {z}}}{2}}$.
3. ${}\operatorname {Im} \,{\left(z\right)}={\frac {z-{\overline {z}}}{2{\mathrm {i} }}}$.

Proof

See Exercise 5.35 .

$\Box$

The square ${}d^{2}$ of a real number is always nonnegative, and the sum of two nonnegative real numbers is again nonnegative. For a nonnegative real number ${}c$ there exists a unique nonnegative square root ${}{\sqrt {c}}$, see Exercise 8.9 Hence the following definition yields a well-defined real number.

Definition

For a complex number

${}z=a+b{\mathrm {i} }\,,$

the modulus is defined by

${}\vert {z}\vert ={\sqrt {a^{2}+b^{2}}}\,.$

The modulus of a complex number ${}z$ is, due to the Pythagorean theorem, the distance of ${}z$ to the zero point ${}0=(0,0)$. The modulus is a mapping

$\mathbb {C} \longrightarrow \mathbb {R} _{\geq 0},z\longmapsto \vert {z}\vert .$

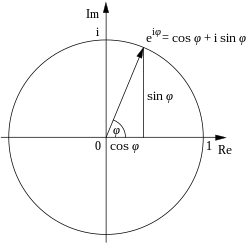
The set of all complex numbers with a certain modulus form a circle with the zero point as center and with the modulus as radius. In particular, all complex numbers with modulus ${}1$ form the complex unit circle. The numbers of the complex unit circle are by the formula of Euler in relation to the complex exponential function and to the trigonometric functions, see Fact ***** and Fact *****. We further mention that the product of two complex numbers of the unit circle may be computed by adding the angles starting from the positive real axis counter clockwise.

Lemma

The modulus of complex numbers

fulfils the following properties.

1. ${}\vert {z}\vert ={\sqrt {z\ {\overline {z}}}}$.
2. For real ${}z$ the real and the complex modulus are the same.
3. We have ${}\vert {z}\vert =0$ if and only if ${}z=0$.
4. ${}\vert {z}\vert =\vert {\overline {z}}\vert$.
5. ${}\vert {zw}\vert =\vert {z}\vert \cdot \vert {w}\vert$.
6. For ${}z\neq 0$ we have ${}\vert {1/z}\vert =1/\vert {z}\vert$.
7. ${}\vert {\operatorname {Re} \,{\left(z\right)}}\vert ,\vert {\operatorname {Im} \,{\left(z\right)}}\vert \leq \vert {z}\vert$.
8. ${}\vert {z+w}\vert \leq \vert {z}\vert +\vert {w}\vert$ (triangle inequality).

Proof

We only show the triangle inequality, for the other statements see Exercise 5.36 . Because of (7) we have for every complex number ${}u$ the estimate ${}\operatorname {Re} \,{\left(u\right)}\leq \vert {u}\vert$. Therefore,

${}\operatorname {Re} \,{\left(z{\overline {w}}\right)}\leq \vert {z}\vert \vert {w}\vert \,,$

and hence

${}{\begin{aligned}\vert {z+w}\vert ^{2}&=(z+w){\left({\overline {z}}+{\overline {w}}\right)}\\&=z{\overline {z}}+z{\overline {w}}+w{\overline {z}}+w{\overline {w}}\\&=\vert {z}\vert ^{2}+2\operatorname {Re} \,{\left(z{\overline {w}}\right)}+\vert {w}\vert ^{2}\\&\leq \vert {z}\vert ^{2}+2\vert {z}\vert \vert {w}\vert +\vert {w}\vert ^{2}\\&=(\vert {z}\vert +\vert {w}\vert )^{2}.\end{aligned}}$

By taking the square root, we get the stated estimate.

$\Box$

<< | Mathematics for Applied Sciences (Osnabrück 2023-2024)/Part I | >> PDF-version of this lecture Exercise sheet for this lecture (PDF)