Mathematics for Applied Sciences (Osnabrück 2023-2024)/Part I/Exercise sheet 13

Exercises

Exercise

Prove the following properties of the hyperbolic sine and the hyperbolic cosine

1. ${}\cosh x+\sinh x=e^{x}\,.$

2. ${}\cosh x-\sinh x=e^{-x}\,.$

3. ${}(\cosh x)^{2}-(\sinh x)^{2}=1\,.$

Exercise

Prove that in the power series ${}\sum _{n=0}^{\infty }c_{n}x^{n}$ of the hyperbolic cosine the coefficients ${}c_{n}$ are ${}0$ if ${}n$ is odd.

Exercise

Show that the hyperbolic sine is strictly increasing on ${}\mathbb {R}$.

Exercise

Prove the addition theorems for the hyperbolic functions, that is,

a)

${}\sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y\,.$

b)

${}\cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y\,.$

Exercise

Prove that the hyperbolic tangent satisfies the following estimate

$-1\leq \tanh x\leq 1{\text{ for all }}x\in \mathbb {R} .$

Exercise

Let

${}P=\sum _{k=0}^{d}a_{k}x^{k}\in \mathbb {R} [X]\,$

be a polynomial. Show that ${}P$ is an odd function if and only if ${}a_{k}=0$ for all even indices.

Exercise

Let ${}f\colon \mathbb {R} \rightarrow \mathbb {R}$ be a function. Where can you recognize, considering the graph of ${}f$, whether ${}f$ is an even function?

Exercise

Let ${}f\colon \mathbb {R} \rightarrow \mathbb {R}$ be a function. Where can you recognize, considering the graph of ${}f$, whether ${}f$ is an odd function?

Exercise

Show that the sum of two even functions is again even, and that the sum of two odd function is again odd. Can you say something about the sum of an even function and an odd function?

Exercise

Show that the product of two even functions is again even, that the product of two odd functions is even, and that the product of an even and an odd function is odd.

Exercise

Show that there exists exactly one function ${}f\colon \mathbb {R} \rightarrow \mathbb {R}$, which is at the same time even and odd.

Exercise

Let

$f\colon \mathbb {R} \longrightarrow \mathbb {R}$

be a continuous function. Show that one can write

${}f=g+h\,,$

with a continuous even function ${}g$ and a continuous odd function ${}h$.

Exercise

What points do you know on the rational unit circle

${}E={\left\{(x,y)\in \mathbb {Q} ^{2}\mid x^{2}+y^{2}=1\right\}}\,?$

Exercise

Describe the upper half of the unit circle and the lower half of the unit circle as graphs of functions.

Exercise

We consider the rational unit circle

${}E={\left\{(x,y)\in \mathbb {Q} ^{2}\mid x^{2}+y^{2}=1\right\}}\,$

and the line

${}G={\left\{(x,y)\in \mathbb {Q} ^{2}\mid x+y=0\right\}}\,.$

1. Determine the intersection points ${}E\cap G$.
2. What is the answer when we consider the situation not over ${}\mathbb {Q}$, but over the real numbers ${}\mathbb {R}$?
3. Can you understand the circle without understanding the the real numbers?
4. Does there exist a relation with the Intermediate value theorem?

Exercise

Determine the coordinates of the two intersection points of the line ${}G$ and the circle ${}K$, where ${}G$ is given by the equation ${}2y-3x+1=0$ and ${}K$ is given by the center ${}(2,2)$ and the radius ${}5$.

Exercise

Determine the intersection points of the unit circle and the line which runs through the points ${}(-1,1)$ and ${}(4,-2)$.

Exercise

Compute the intersection points of the two circles ${}K_{1}$ and ${}K_{2}$, where ${}K_{1}$ has center ${}(3,4)$ and radius ${}6$ and ${}K_{2}$ has center ${}(-8,1)$ and radius ${}7$.

Exercise

Let ${}a,b,r\in \mathbb {R}$, ${}r>0$, and let

${}K={\left\{(x,y)\in \mathbb {R} ^{2}\mid (x-a)^{2}+(y-b)^{2}=r^{2}\right\}}\,$

be the circle with center ${}M=(a,b)$ and radius ${}r$. Let ${}G$ denote a line in ${}\mathbb {R} ^{2}$ with the property that there exists at least one point ${}P$ on ${}G$ such that ${}d(M,P)\leq r$. Show that ${}K\cap G\neq \emptyset$.

Exercise

We consider a circle (with radius ${}1$) and regular ${}n$-gons inscribed in the circle.

1. 

   Suppose that a square is inscribed in the circle. Determine its area and its perimeter.

2. 

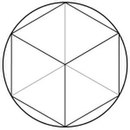
   Suppose that a regular ${}6$-gon is inscribed. Determine its area and its perimeter.

3. The area of an inscribed regular ${}n$-gon is an approximation for the area of the circle and its perimeter is an approximation for the circumference of the circle. Which one is better?

Exercise

Prove by elementary geometric considerations the Sine theorem, i.e. the statement that in a triangle the equalities

${}{\frac {\sin \alpha }{a}}={\frac {\sin \beta }{b}}={\frac {\sin \gamma }{c}}\,$

hold, where ${}a,b,c$ are the side lengths of the edges and ${}\alpha ,\beta ,\gamma$ are respectively the opposite angles.

Exercise

We look at a clock with minute and second hands, both moving continuously. Determine a formula which calculates the angular position of the second hand from the angular position of the minute hand (each starting from the 12-clock-position measured in the clockwise direction).

Exercise

Dr. Eisenbeis wants to build a bicycle-ramp for her nephews Richy and Franky. The ramp shall rise along a circle arc of the length (everything in meter) ${}\ell =1,2$ and reach a jumping height of ${}h=0,2$ (see image). What (implicit) condition does the angle ${}\alpha$ fulfill (the condition on ${}\alpha$ must be such that it could be solved using the bisection method, but this need not be performed)?

Exercise

Determine the coefficients up to ${}z^{6}$ in the series product ${}\sum _{n=0}^{\infty }c_{n}z^{n}$ of the sine series and the cosine series.

Exercise

Compute

${\left(1-{\frac {1}{2}}X^{2}+{\frac {1}{24}}X^{4}\right)}^{2}+{\left(X-{\frac {1}{6}}X^{3}+{\frac {1}{120}}X^{5}\right)}^{2}.$

Is the result surprising, how can you explain it?

Exercise

Show that ${}-1\leq \sin x\leq 1$ and ${}-1\leq \cos x\leq 1$ holds for all ${}x\in \mathbb {R}$.

Exercise

Determine the limit of the sequence

${\frac {\sin n}{n}},\,n\in \mathbb {N} _{+}.$

Exercise

Prove that the series

$\sum _{n=1}^{\infty }{\frac {\sin n}{n^{2}}}$

converges.

Hand-in-exercises

Exercise (3 marks)

Prove that the hyperbolic cosine is strictly decreasing on ${}\mathbb {R} _{\leq 0}$ and strictly increasing on ${}\mathbb {R} _{\geq 0}$.

Exercise (3 marks)

Determine the coordinates of the two intersection points of the line ${}G$ and the circle ${}K$, where ${}G$ is given by the equation ${}3y-4x+2=0$ and ${}K$ is given by the center ${}(2,5)$ and the radius ${}7$.

Exercise (6 marks)

We consider the unit circle, i.e.

${}{\left\{{\begin{pmatrix}x\\y\end{pmatrix}}\mid x^{2}+y^{2}=1\right\}}\subseteq \mathbb {R} ^{2}\,.$

We put ${}P_{0}={\begin{pmatrix}1\\0\end{pmatrix}}$ and ${}P_{1}={\begin{pmatrix}0\\1\end{pmatrix}}$, and we define recursively the sequence ${}P_{n}$ (in the plane) by

${}Q_{n}={\frac {1}{2}}{\left(P_{0}+P_{n-1}\right)}\,$

(that is, ${}Q_{n}$ is the bisection point of the line segment between ${}P_{0}$ and ${}P_{n-1}$), and ${}P_{n}$ is the intersection point of the half-line through ${}{\begin{pmatrix}0\\0\end{pmatrix}}$ and ${}Q_{n}$ and the circle. We consider the lengths ${}d_{n}=d(P_{0},P_{n})$ as an approximation for the length of the circle arc between ${}P_{0}$ and ${}P_{n}$, and therefore

${}x_{n}=2^{n}d_{n}\,$

is an approximation for the length of the half circle arc (that is, ${}\pi$). Since in the computation of the points ${}P_{n}$ and the lengths ${}d_{n}$, square roots occure (due to the Pythagorean theorem), we can approximate these by rational numbers only with certain errors.

Write a computer-program (in pseudocode), which computes and prints a sequence ${}y_{n}$ of approximations (${}n\geq 1$) for ${}x_{n}$. In the computation of ${}y_{n}$, all square roots, which are used in the computation of ${}x_{n}$, shall be computed with ${}n$ steps of Heron's method, starting with the initial value ${}1$. Also, the program shall use better and better approximations for the auxiliary points, the computation of ${}y_{n}$ requires that better and better approximations for ${}P_{2},\ldots ,P_{n}$ are determined.

• The computer has as many memory units as needed, which can contain rational numbers.
• The natural numbers are provided in a data base (they do not have to be computed).
• It can write the content of a memory unit into another memory unit.
• It can do the arithmetic operations (addition, subtraction, multiplication, division by a number ${}\neq 0$) on rational numbers and write the result in another memory unit.
• It can compare the content of memory units and can, depending on the outcome, switch to a certain program line.
• It can print contents of memory units and it can print given texts.

The program shall run to infinity and write down the approximations ${}y_{1},y_{2},y_{3},...$.

Exercise (5 marks)

Prove the addition theorem

${}\sin(x+y)=\sin x\cdot \cos y+\cos x\cdot \sin y\,$

for the sine using the defining power series.

Exercise (3 marks)

Decide whether the sequence defined by

${}x_{n}:={\frac {5\sin ^{3}n-6n^{4}+13n^{2}+{\left(\sin n\right)}{\left(\cos {\left(n^{2}\right)}\right)}}{7n^{4}-5n^{3}+n^{2}\sin ^{2}{\left(n^{3}\right)}-\cos n}}\,$

converges in ${}\mathbb {R}$ and determine, if applicable, the limit.

Exercise (5 marks)

Consider ${}n$ complex numbers ${}z_{1},z_{2},\ldots ,z_{n}$ lying in the disc ${}B$ with center ${}(0,0)$ and radius ${}1$, that is in ${}B={\left\{z\in \mathbb {C} \mid \vert {z}\vert \leq 1\right\}}$. Prove that there exists a point ${}w\in B$ such that

${}\sum _{i=1}^{n}\vert {z_{i}-w}\vert \geq n\,.$

<< | Mathematics for Applied Sciences (Osnabrück 2023-2024)/Part I | >> PDF-version of this exercise sheet Lecture for this exercise sheet (PDF)