Laurent Series

Introduction

This page about Laurent Series can be displayed as Wiki2Reveal slides. Single sections are regarded as slides and modifications on the slides will immediately affect the content of the slides. The following aspects of Laurent Series are considered in detail:

f(x)=\sum _{n=-\infty }^{\infty }c_{n}(x-a)^{n}

${\textstyle c_{n}}$ coefficients
${\textstyle a}$ development point of series

Main Part and Regular Part

The series of terms with negative exponents is called the main part of the Laurent series, and the series of terms with non-negative exponents is called the regular part or the residual part.

Connection to Power Series

A Laurent series with a vanishing main part is a power series; if it also has only finitely many terms, then it is a polynomial. If a Laurent series has only finitely many terms in total (with negative or positive exponents), it is called a Laurent polynomial.

History

The Laurent series was introduced in 1843 by the French mathematician Pierre Alphonse Laurent. However, notes in the legacy of the German mathematician Karl Weierstrass suggest that he discovered it as early as 1841.

Laurent Decomposition

The principle of developing a holomorphic function into a Laurent series is based on the Laurent decomposition. To do this, consider an annular region ${\mathcal {R}}={z\in \mathbb {C} ;|;r<|z|<R}$ . Now define two holomorphic functions $g$ and $h$ :

g\colon U_{R}(0)\rightarrow \mathbb {C}

h\colon U_{\frac {1}{r}}(0)\rightarrow \mathbb {C}

.

Representation of Laurent Series by Two Holomorphic Functions

Let $g:G\rightarrow \mathbb {C}$ and $h:G\rightarrow \mathbb {C}$ be two holomorphic functions with a development point $z_{0}\in G$ ,

f(z):=g(z-z_{0})+{\hat {h}}(z-z_{0})

with

{\hat {h}}(z):=h(1/z)

.

$g$ and $h$ are holomorphic functions on $G_{0}:={z-z_{0}\in \mathbb {C} \ |\ z\in G}$ , which can be developed into a power series around 0 in $G_{0}$ .

Convergence Set of Laurent Series

The functions $g$ and $h$ can be locally represented as a power series on a disk in $G_{o}:={z-z_{o}\in \mathbb {C} \ |\ z\in G}$ (holomorphy criterion). Then ${\hat {h}}$ with ${\hat {h}}(z):=h(1/z)$ converges on the complement of a disk.

Intersection of Convergence Domains

If $f(z)$ 's principal part $g(z)$ and ${\hat {h}}(z)$ are convergent, then $z$ lies in the intersection of the convergence sets. If $r>R$ , the convergence set is empty because $z$ would simultaneously have to lie on a disk of radius $R$ and on the complement of a disk with radius $r$ .

Convergence Radii

Let $R_{g}>0$ and $R_{h}>0$ be the convergence radii for the functions $g$ and $h$ . Calculate the radius $R_{\hat {h}}>0$ of the convergence set of ${\hat {h}}(z):=h(1/z)$ for all $z\in G_{o}$ with $|z|>R_{\hat {h}}>0$ .

Geometry of the Convergence Set

$h$ converges holomorphically around the center on the disk with radius $1/r$ . Since the argument of the function $h$ must lie within the defined circular region, it quickly becomes evident that the function $h(1/z)$ is defined for values $|z|>r$ . Thus, the sum of the two functions

f(z)=g(z)+h\left({\frac {1}{z}}\right)

is analytic on the annulus ${\mathcal {R}}$ .

Uniqueness of Decomposition

It can be shown that any holomorphic function on an annular domain can be decomposed in this way. If one also assumes $h(0)=0$ , the decomposition is unique.

By expanding this function in the form of power series, the following representation arises:

f(z)=g(z)+h\left({\frac {1}{z}}\right)=\sum _{n=0}^{\infty }a_{n}z^{n}+\sum _{n=1}^{\infty }b_{n}z^{-n}=\sum _{n=-\infty }^{\infty }a_{n}z^{n}

.

Here, $b_{n}\equiv a_{-n}$ is defined. Additionally, $b_{0}=0$ follows from the condition $h(0)=0$ .

Decomposition with Expansion Point

If these considerations are extended to an expansion around a point $c$ , rather than the origin, the initially stated definition of the Laurent series for a holomorphic function $f$ around the expansion point $c$ results:

f(z)=\sum _{n=-\infty }^{\infty }a_{n}(z-c)^{n}

Example

In the following, ${\textstyle \mathbb {K} }$ refers to either the real numbers or the complex numbers.

f\colon \mathbb {K} \to \mathbb {K} \colon x\mapsto {\begin{cases}\exp \left(-{\frac {1}{x^{2}}}\right),&x\neq 0\ 0,&{\text{otherwise}}\end{cases}}

.

The function is infinitely often differentiable in the real sense, but it is not holomorphic at $x=0$ , where it has an essential singularity.

Substituting into the Taylor Series

By substituting ${\textstyle z=-{\frac {1}{x^{2}}}}$ into the power series expansion of the exponential function,

e^{z}=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}=\sum _{n=0}^{\infty }{\frac {\left(-{\frac {1}{x^{2}}}\right)^{n}}{n!}}

the Laurent series of ${\textstyle f}$ with the expansion point ${\textstyle 0}$ is obtained:

f(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{-2n}}{n!}}=\underbrace {\sum _{n=-\infty }^{-1}{\frac {(-1)^{n}}{(-n)!}}x^{2n}} _{\text{Principal part}}+1

Convergence Domain of the Laurent Series

The secondary part $g(x)=1$ converges throughout $\mathbb {C}$ , and the principal part (and therefore the entire Laurent series) converges for every complex number ${\textstyle x\neq 0}$ .

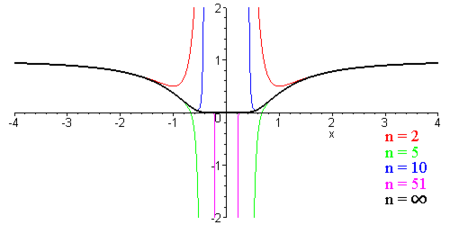
Approximation of the Function by Partial Sums

The image shows how the partial sum sequence

f_{n}(x)=\sum _{j=0}^{n}(-1)^{j}{\frac {x^{-2j}}{j!}}

approaches the function.

Comparison of Graphs of Partial Sums with the Function

.

Since graphs in $\mathbb {C}$ are subsets of 4-dimensional $\mathbb {R}$ -vector spaces, the graph is plotted here for values $x\in \mathbb {R} \setminus {0}$ . The Laurent expansion can be continuously extended at 0.

Convergence of Laurent Series

Laurent series are important tools in complex analysis, especially for studying functions with isolated singularities.

Annuli and Disks

Laurent series describe complex functions that are holomorphic on an annulus, just as power series describe functions holomorphic on a disk.

Let

\sum _{n=-\infty }^{\infty }a_{n}(z-c)^{n}

be a Laurent series in $z$ with complex coefficients $a_{n}$ and expansion point $c$ .

Convergence Radii - Interior of the Annulus

There are two uniquely determined numbers $r$ and $R$ such that:

The Laurent series converges uniformly and absolutely on the open annulus $A:={z:r<\vert z-c\vert <R}$ .

It converges normally, meaning the principal and secondary parts converge normally. This defines a holomorphic function $f$ on $A$ .

Outside the Annulus

Outside the annulus, the Laurent series diverges. For every point in

\mathbb {C} \setminus {\overline {A}}:={z:r>\vert z-c\vert \vee \vert z-c\vert >R}

,

either the terms with positive (secondary part) or negative exponents (principal part) diverge.

Convergence Radii and Cauchy-Hadamard

The two radii can be calculated using the Cauchy-Hadamard formula:

r=\limsup _{n\to \infty }\vert a_{-n}\vert ^{1/n}

R={\frac {1}{\limsup _{n\to \infty }\vert a_{n}\vert ^{1/n}}}

We set ${\frac {1}{0}}=\infty$ and ${\frac {1}{\infty }}=0$ in the second formula.

Functions Defined on Annuli

Conversely, one can start with an annulus $A:={z:r<\vert z-c\vert <R}$ and a function $f$ that is holomorphic on $A$ . Then, there always exists a uniquely determined Laurent series with expansion point $c$ that converges (at least) on $A$ and coincides with $f$ there. The coefficients satisfy:

a_{n}={\frac {1}{2\pi \mathrm {i} }}\oint _{\partial U_{\varrho }(c)}{\frac {f(\zeta )}{\left(\zeta -c\right)^{n+1}}}\mathrm {d} \zeta

for all $n\in \mathbb {Z}$ and a $\varrho \in (r,R)$ . Due to the Cauchy integral theorem, the choice of $\varrho$ does not matter.

Punctured Disk

The case $r=0$ , i.e., a holomorphic function $f$ on a punctured disk around $c$ , is particularly important. The coefficient $a_{-1}$ in the Laurent series expansion of $f$ is called the residue of $f$ at the isolated singularity $c$ . It plays a significant role in the residue theorem.

Formal Laurent Series

Formal Laurent series are Laurent series in the indeterminate $X$ , used without consideration of convergence.

Laurent Series on Commutative Rings

The coefficients $a_{k}$ can then belong to any commutative ring. In this context, it only makes sense to consider Laurent series with finitely many negative exponents, known as a "finite principal part," and to omit the expansion point by setting $c=0$ .

Equality of Formal Laurent Series

Two such formal Laurent series are defined as equal if and only if all their coefficients agree. Laurent series are added by summing their respective coefficients. Since there are only finitely many terms with negative exponents, they can be multiplied by convolution of their coefficient sequences, similar to power series. With these operations, the set of all Laurent series over a commutative ring $R$ forms a commutative ring, denoted by $R\left(!\left(X\right)!\right)$ .

Laurent Series and Integral Domains

If $K$ is a field, the formal power series in the indeterminate $X$ over $K$ form an integral domain, denoted by $K\left[!\left[X\right]!\right]$ . Its field of fractions is isomorphic to the field $K\left(!\left(X\right)!\right)$ of Laurent series over $K$ .

Exercises

Let $K_{r_{1},r_{2}}:={z\in \mathbb {C} ,|,r_{1}<|z|<r_{2}}$ . Construct a Laurent series with this annulus as its domain of convergence, which does not converge on $\mathbb {C} \setminus {\overline {K_{r_{1},r_{2}}}}$ . Use geometric series as an idea with $\sum _{n=0}^{+\infty }q^{n}$ converging for $q\in \mathbb {C}$ when $|q|<1$ .

Exercises on Laurent Series and b-adic Number Systems

Analyze the relationship between Laurent series and the p-adic number system (e.g., binary system, hexadecimal system)! What are the similarities and differences?

Represent the number ${\frac {1}{7}}$ as a value of a Laurent series in the 4-based number system $x=4$ , where $c_{n}\in {0,1,2,3}$ . Calculate the coefficients $c_{n}$ :

f(x):=\sum _{n=-\infty }^{+\infty }c_{n}\cdot z^{n}

z

Literature

Eberhard Freitag & Rolf Busam: Complex Analysis 1, Springer-Verlag, Berlin, ISBN 3-540-67641-4

Page Information

You can display this page as Wiki2Reveal slides

Wiki2Reveal

The Wiki2Reveal slides were created for the Complex Analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.

This page is designed as a PanDocElectron-SLIDE document type.
Source: Wikiversity https://en.wikiversity.org/wiki/Laurent%20Series
see Wiki2Reveal for the functionality of Wiki2Reveal.

Translation and Version Control

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

Source: Laurent-Reihe - URL: https://de.wikiversity.org/wiki/Laurent-Reihe
Date: 12/17/2024