Gears
Gears are toothed wheels which are used to transmit force to other gears or toothed parts by meshing with minimal slip.
When two gears are meshed together, the smaller gear is called a pinion. The gear transmitting force is referred to as a drive gear, and the receiving gear is called the driven gear.
When pinion is the driver, it results in step down drive in which the output speed decreases and the torque increases. On the other hand, when the gear is the driver, it results in step up drive in which the output speed increases and the torque decreases.
History
[edit | edit source]Types
[edit | edit source]| Spur gears
Spur gears are the simplest of all the gears.They have their tooth parallel to the axis. They are used for transmitting power between two parallel shafts.They also have high efficiency and high precision rating.So,they are used for high speed and high load applications An example of spur gear application would be its usage in a gear box of a motorcycle |
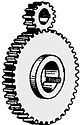 |
| Helical gears
Helical gears are used for parallel shaft drives. Their teeth are inclined to the axis and hence for the same width, their teeth are longer than spur gears. Their contact ratio (the average number of teeth in contact at any one time) is therefore higher than that of spur gears, which allows increased capacity (better load sharing) and a smoother and quieter operation. Due to the tooth inclination, helical gears tend to create axial forces, in addition to transverse and radial loads. This can have undesirable effects on bearing life, but can be overcome to some degree in multiple step transmissions by alternating the inclination of helix on gears that share the same shaft. Helical gears also are used in automotive gear boxes |
 |
| Herringbone or Double helical gears
These gears are also used for transmitting power between two parallel shafts. They have two opposing tooth helix's on the circumference. These opposing helix angles enables this type of gear to nullify more axial loads. Their load capacity is very high but manufacturing difficulty makes them more costly. These gears are used in cement mills and crushers. |
 |
| Internal gears
Internal gears have their tooth engraved in the inner periphery.These gears also are used in transmitting power between parallel shafts. Internal gears are used in planetary gear drives of automotive transmission reduction,gear boxes of cement mills,step up drives of windmills etc. |
 |
| Rack and pinion
Rack is a linear gear.The gear which meshes with it is called a pinion.The tooth can be of either helical or spur type.These type of gears are used in converting circular motion to linear and vice versa. Carriage movement in lathes is produced by using rack and pinion |
 |
| Straight bevel gears
These gears are used for transmitting power between intersecting shafts at different angles of which most common are those at right angles. Straight bevel gears are used in a final drive with a differential |
 |
| Spiral bevel gears
|
Plastic gears
Gear tooth system
[edit | edit source]A gear tooth system is defined by its unique tooth proportions,pressure angles etc.
Law of gearing
[edit | edit source]Before we take a look at the actual gearing systems let us see what is the fundamental law that governs the gearing system. The law of gearing states that
the angular velocity ratio of all gears of a meshed gear system must remain constant also the common normal at the point of contact must pass through the pitch point.
Example: if and are the angular velocities and and are the diameters of two gears meshed together then [1]
Gear profiles
[edit | edit source]Gear profiles should satisfy the law of gearing.
The profiles best suited for this law are:
Gear Nomenclature
[edit | edit source]Various nomenclatures related to a gear are shown in the figure

- Let us consider a spur gear and define the following terms-
- Pitch circle:Can roughly be defined as the circle having radius as the mean of the maximum radius(to the tip of the gear teeth) to the radius of the base of a gear tooth. However tooth proportions can vary considerably, with both root and tip adjusted to suit running conditions and manufacturing processes, making this definition somewhat unreliable.
- Addendum:The tooth portion above the pitch circle (towards the tooth tip).
- Dedendum:The tooth portion below the pitch circle (towards the tooth root).
- Flank:The face of a gear tooth which comes in contact with the teeth of another gear. So,a flank is an important part of a gear.
- Fillet:Fillets in the root region are of less importance since they don't come into contact with other gear teeth. However root fillets are of great importance with regard to tooth bending strength, and therefore power ratings. Gears with little or no fillet in the root are prone to tooth breakage, as the sharp corner acts as a stress raiser.
- Circular pitch:The sum of the width of a tooth and a space between the tooth of a gear. Circular pitch is an important parameter as it indicates the size of the tooth of a gear.If is the circular pitch,Z is the number of teeth on a gear and D is the pitch diameter then,
So the size of a tooth is given by where m is the unit of size called module.And hence for two meshed gears we must have the same size of tooth,then we can have the following relations, ---(1)
In case of a rack the diameter and the number of tooth tend to infinity but still the module remain finite.
- Circular thickness or tooth thickness: It is the thickness of the tooth measured on the pitch circle.It should be noted that this thickness is measured as the arc along the pitch circle and should not be taken as the displacement
- Diametral Pitch: It is defined as the number of tooth per inch of the diameter of the pitch circle of a gear.It is indicated by the letter P.Therefore, ---(2)
So using equation (1) and (2), we can have











