Equivalence relation/Quotient set/Section

Definition

Let ${}R\subseteq M\times M$ denote an equivalence relation. The set

${}M/R:={\left\{[x]\mid x\in M\right\}}\,$

is called the quotient set of ${}R$.

Definition

Let ${}R\subseteq M\times M$ denote an equivalence relation, and let ${}M/R$ be the quotient set. The mapping

$q_{R}\colon M\longrightarrow M/R,x\longmapsto [x],$

is called the canonical projection of ${}R$.

With the quotient set, the equivalence classes become elements of a new set. Under the canonical projection, equivalent elements are mapped to the same element and so they are identified. We also say that the theory of equivalence relations is the art of identifying. In working with quotient sets, the proper definition is not so important any more; instead, we work rather with the intrinsic properties of these sets. The following statement says, in particular, that every equivalence relation can be obtained as in example. Therefore, equivalent always means equal under a suitable mapping.

Lemma

Let ${}M$ be a set, and let ${}\sim$ denote an equivalence relation on ${}M$, together with the equivalence classes ${}[x]$ and the quotienten set

${}M/\sim$. Then the following statements hold.

1. ${}x\sim y$ if and only if ${}[x]=[y]$, and this holds if and only if ${}[x]\cap [y]\neq \emptyset$.
2. ${}M=\bigcup _{[x]\in M/\sim }[x]$ is a disjoint union.
3. The canonical projection

   $q\colon M\longrightarrow M/\sim ,x\longmapsto [x],$

   is surjective.

4. We have ${}q^{-1}([x])=[x]$.

Proof

1. Let ${}x$ and ${}y$ be equivalent, and ${}u\in [x]$. Then ${}x\sim u$, and, by transitivity, also ${}y\sim u$, thus ${}u\in [y]$. Therefore, the equivalence classes coincide. The implication from the middle to the right is clear, because, due to ${}x\sim x$, the equivalence classes are not empty. Suppose now that ${}[x]\cap [y]\neq \emptyset$, and let ${}z$ denote an element in the intersection. Then ${}x\sim z$ and ${}y\sim z$, and, by transitivity, ${}x\sim y$.
2. Because of the reflexivity, we have ${}x\in [x]$; therefore, ${}M=\bigcup _{[x]\in M/\sim }[x]$. This union is disjoint by part (1).
3. The surjectivity is clear because of the definition of the quotient set, and since ${}x$ is sent to the class ${}[x]$.
4. We have

   ${}q^{-1}([x])={\left\{y\in M\mid q(y)=[x]\right\}}={\left\{y\in M\mid [y]=[x]\right\}}={\left\{y\in M\mid y\sim x\right\}}=[x]\,.$

$\Box$

Important mathematical constructions can be described as a quotient set to a certain equivalence relation on a simpler set. This is illustrated by the following examples.

Example

Let ${}n\in \mathbb {N}$, and set ${}M=\mathbb {R} ^{n+1}\setminus \{0\}$. ${}\mathbb {R} ^{n+1}$ is a real vector space, the scalar multiplication of ${}\lambda \in \mathbb {R}$ and ${}x\in \mathbb {R} ^{n+1}$ is denoted by ${}\lambda \cdot x$ Moreover, set

$R={\left\{(x,y)\in M\times M\mid {\text{ there exists some }}\lambda \in \mathbb {R} \setminus \{0\}{\text{ such that }}\lambda \cdot x=y\right\}}\,.$

Therefore, two points are defined to be equivalent if they can be transformed to each other by scalar multiplication with a scalar ${}\lambda \neq 0$. We can also say that two points are equivalent if they define the same line through the origin.

This is indeed an equivalence relation. The reflexivity follows from ${}x=1x$ for every ${}x\in M$. To prove symmetry, suppose ${}xRy$, that is, there exists some ${}\lambda \neq 0$ such that ${}\lambda x=y$. Then also ${}y=\lambda ^{-1}x$ holds, as ${}\lambda$ has an inverse element. To prove transitivity, suppose that ${}xRy$ and ${}yRz$ holds; this means that there exist ${}\lambda ,\delta \neq 0$ such that ${}\lambda x=y$ and ${}\delta y=z$. Then ${}z=\delta y=(\delta \lambda )x$ with ${}\delta \lambda \neq 0$. The equivalence classes of this equivalence relation are the lines through the origin (but without the origin). The quotient set is called the real-projective space (of real dimension ${}n$), and is denoted by ${}{\mathbb {P} }_{\mathbb {R} }^{n}$.

Example

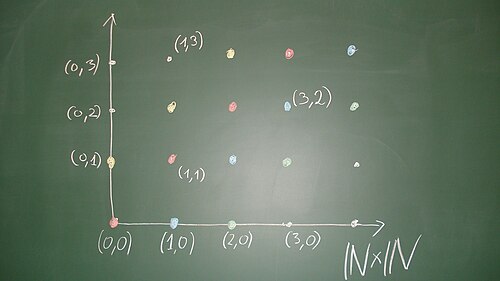
Let ${}\mathbb {N}$ be the set of the natural numbers, and let ${}M=\mathbb {N} \times \mathbb {N}$ denote the product set with the componentwise addition. We define on ${}M$ a relation by

$(a,b)\sim (c,d),{\text{ if }}a+d=b+c.$

This holds, in case ${}a\leq c$, if and only if there exists an ${}e\in \mathbb {N}$ (namely ${}e=c-a$) such that

${}(c,d)=(a,b)+(e,e)\,.$

This means that the pairs differ by an diagonal element, that is, a pair, where both components coincide. This relation is an equivalence relation on ${}M$, see exercise. If we consider ${}\mathbb {N} \times \mathbb {N}$ as a square lattice (a "discrete coordinate system“), then the equivalence classes are given by the points on a "discrete line“ parallel to the diagonal. The points ${}(a,b)$ with ${}a\geq b$ are equivalent with ${}(a-b,0)$; they have a representative where the second component is ${}0$. The points ${}(a,b)$ with ${}a\leq b$ are equivalent to ${}(0,b-a)$; they have a representative where the first component is ${}0$. The points ${}(a,a)$ are equivalent to ${}(0,0)$. We call the representative of an equivalence class where at least one component is ${}0$, the standard representative of this equivalence class. The standard representatives are the discrete points of the confining lines of the quadrant; for a point, we find its standard representative by going, parallel to the diagonal, in direction of these lines. Two points are equivalent if and only if they have the same standard representative.

We call now the quotient set, that is, the set of the equivalence classes under this equivalence relation, the set of the integer numbers, and denote it with ${}\mathbb {Z}$. Every integer number has exactly one standard representative of the form ${}n:=(n,0)$ with ${}n\in \mathbb {N} _{+}$, or of the form ${}0:=(0,0)$, or of the form ${}-n:=(0,n)$ with ${}n\in \mathbb {N} _{+}$. We consider a natural number ${}n$ as the integer number ${}(n,0)$.

We want to "add“ two integer numbers, that is, two such equivalence classes ${}[(a,b)]$ and ${}[(c,d)]$, in order to get a binary operation ${}\oplus$ on ${}\mathbb {Z}$. The first idea that comes to mind is to define this via

${}[(a,b)]\oplus [(c,d)]:=[(a+c,b+d)]\,.$

However, here we encounter the problem whether this is well-defined, since this operation is defined using certain representatives; it is not clear at all whether different representatives give the same result. Therefore, if ${}(a,b)\sim (a',b')$ and ${}(c,d)\sim (c',d')$ holds, then we have to check that also

${}(a+c,b+d)\sim (a'+c',b'+d')\,$

holds, which means ${}[(a+c,b+d)]=[(a'+c',b'+d')]$. This is the case, see exercise. Moreover, one can show that this operation on ${}\mathbb {Z}$ is associative and commutative, that ${}[(0,0)]$ is the neutral element of this operation, and that for every element ${}[(a,b)]$ there exists an inverse element, namely ${}[(b,a)]$.

We define now a multiplication on ${}\mathbb {Z}$ via

${}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,.$

Again, this is well-defined, and one can show that the multiplication is associative and commutative, that ${}1=[(1,0)]$ is the neutral element, and that the distributive law holds.

The following proposition describes the universal property of the quotient set.

Lemma

Let ${}M$ be a set, and let ${}\sim$ denote an equivalence relation on ${}M$, with the quotient set ${}M/\sim$. Let ${}\varphi \colon M\rightarrow W$ be a mapping with ${}\varphi (x)=\varphi (y)$ for all ${}x,y\in M$ with ${}x\sim y$. Then there exists a uniquely determined mapping ${}{\overline {\varphi }}\colon M/\sim \,\,\rightarrow W$ fulfilling

${}\varphi ={\overline {\varphi }}\circ q$.

Proof

Let ${}[x]\in M/\sim$ be given. The only possibility for ${}{\overline {\varphi }}$ is to set ${}{\overline {\varphi }}([x]):=\varphi (x)$. We have to show that this mapping is well-defined, that is, independent of the choice of the representatives. For this, let ${}[x]=[y]$, that is, ${}x\sim y$. By the condition on ${}\varphi$, we have ${}\varphi (x)=\varphi (y)$.

$\Box$