Integer numbers/Construction from natural numbers/Example
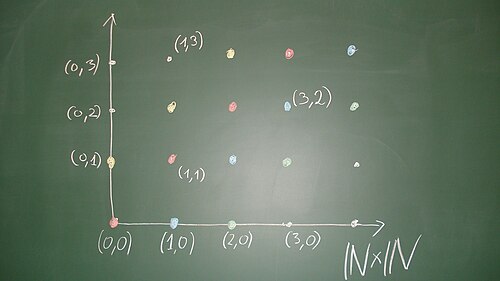
Let be the set of the natural numbers, and let denote the product set with the componentwise addition. We define on a relation by
This holds, in case , if and only if there exists an (namely ) such that
This means that the pairs differ by an diagonal element, that is, a pair, where both components coincide. This relation is an equivalence relation on , see exercise. If we consider as a square lattice (a "discrete coordinate system“), then the equivalence classes are given by the points on a "discrete line“ parallel to the diagonal. The points with are equivalent with ; they have a representative where the second component is . The points with are equivalent to ; they have a representative where the first component is . The points are equivalent to . We call the representative of an equivalence class where at least one component is , the standard representative of this equivalence class. The standard representatives are the discrete points of the confining lines of the quadrant; for a point, we find its standard representative by going, parallel to the diagonal, in direction of these lines. Two points are equivalent if and only if they have the same standard representative.
We call now the quotient set, that is, the set of the equivalence classes under this equivalence relation, the set of the integer numbers, and denote it with . Every integer number has exactly one standard representative of the form with , or of the form , or of the form with . We consider a natural number as the integer number .
We want to "add“ two integer numbers, that is, two such equivalence classes and , in order to get a binary operation on . The first idea that comes to mind is to define this via
However, here we encounter the problem whether this is well-defined, since this operation is defined using certain representatives; it is not clear at all whether different representatives give the same result. Therefore, if and holds, then we have to check that also
holds, which means . This is the case, see exercise. Moreover, one can show that this operation on is associative and commutative, that is the neutral element of this operation, and that for every element there exists an inverse element, namely .
We define now a multiplication on via
Again, this is well-defined, and one can show that the multiplication is associative and commutative, that is the neutral element, and that the distributive law holds.

























![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a)
![{\displaystyle {}[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b865712c6f9654641f6315839d7fb250d5ed6fa1)

![{\displaystyle {}[(a,b)]\oplus [(c,d)]:=[(a+c,b+d)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a0f3b6534a2c47aafd828302970887624130373)



![{\displaystyle {}[(a+c,b+d)]=[(a'+c',b'+d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9bc368eabf53b7c89081c97a70ea09b665f4fb)
![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9)
![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e886953fa3c1d350ffa773ec3c5eee3948d2a80c)
![{\displaystyle {}1=[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7def7a0131953ef73e591cb841fb440c9b19b53b)