Complex numbers/Real part, conjugation, modulus/Introduction/Section

Definition

The set ${}\mathbb {R} ^{2}$ with ${}0:=(0,0)$ and ${}1:=(1,0)$, with componentwise addition and the multiplication defined by

${}(a,b)\cdot (c,d):=(ac-bd,ad+bc)\,,$

is called the field of complex numbers. We denote it by

$\mathbb {C} .$

So the addition is just the vector addition in ${}\mathbb {R} ^{2}$, but the multiplication is a new operation. We will see in fact a more geometric interpretation for the complex multiplication.

Lemma

The complex numbers form a field.

Proof

See exercise.

$\Box$

From now on we write

${}a+b{\mathrm {i} }:=(a,b)\,$

and in particular we put ${}{\mathrm {i} }=(0,1)$, this number is called the imaginary unit. It has the important property

${}{\mathrm {i} }^{2}=-1\,.$

From this property and the rules of a field, one can deduce all algebraic properties of the complex numbers. This also helps in memorizing the multiplication rule as we have

${}(a+b{\mathrm {i} })(c+d{\mathrm {i} })=ac+ad{\mathrm {i} }+b{\mathrm {i} }c+b{\mathrm {i} }d{\mathrm {i} }=ac+bd{\mathrm {i} }^{2}+(ad+bc){\mathrm {i} }=ac-bd+(ad+bc){\mathrm {i} }\,.$

We consider a real number ${}a$ as the complex number ${}a+0{\mathrm {i} }=(a,0)$. Hence ${}\mathbb {R} \subset \mathbb {C}$. It does not make a difference whether we add or multiply real numbers as real numbers or as complex numbers.

Definition

For a complex number

${}z=a+b{\mathrm {i} }\,,$

we call

${}\operatorname {Re} \,{\left(z\right)}=a\,$

the real part of ${}z$ and

${}\operatorname {Im} \,{\left(z\right)}=b\,$

the imaginary part of ${}z$.

However, one should not think that complex numbers are less real than real numbers. The construction of the complex numbers starting from the reals is by far easier than the construction of the real numbers starting from the rational numbers. On the other hand, it was a long historic process until complex numbers were accepted as numbers; they form a field, but not an ordered field, and so at first glance they are numbers which do not measure anything.

One should think of complex numbers as points of the plane; for the additive structure we have directly ${}\mathbb {C} =\mathbb {R} ^{2}$. The horizontal axis is called the real axis and the vertical axis is called the imaginary axis.

Lemma

The real part and the imaginary part of complex numbers fulfill the following properties (for

${}z$ and ${}w$ in ${}\mathbb {C}$).

1. ${}z=\operatorname {Re} \,{\left(z\right)}+\operatorname {Im} \,{\left(z\right)}{\mathrm {i} }$.
2. ${}\operatorname {Re} \,{\left(z+w\right)}=\operatorname {Re} \,{\left(z\right)}+\operatorname {Re} \,{\left(w\right)}$.
3. ${}\operatorname {Im} \,{\left(z+w\right)}=\operatorname {Im} \,{\left(z\right)}+\operatorname {Im} \,{\left(w\right)}$.
4. For ${}r\in \mathbb {R}$ we have

   $\operatorname {Re} \,{\left(rz\right)}=r\operatorname {Re} \,{\left(z\right)}{\text{ and }}\operatorname {Im} \,{\left(rz\right)}=r\operatorname {Im} \,{\left(z\right)}.$

5. ${}z=\operatorname {Re} \,{\left(z\right)}$ holds if and only if ${}z\in \mathbb {R}$ holds, and this holds if and only if ${}\operatorname {Im} \,{\left(z\right)}=0$ holds.

Proof

See exercise.

$\Box$

Definition

The mapping

$\mathbb {C} \longrightarrow \mathbb {C} ,z=a+b{\mathrm {i} }\longmapsto {\overline {z}}:=a-b{\mathrm {i} },$

is called complex conjugation.

For ${}z$, the number ${}{\overline {z}}$ is called the complex-conjugated number of ${}z$. Geometrically, the complex conjugation to ${}z\in \mathbb {C}$ is simple the reflection at the real axis.

Lemma

For the complex conjugation, the following rules hold (for arbitrary

${}z,w\in \mathbb {C}$).

1. ${}{\overline {z+w}}={\overline {z}}+{\overline {w}}$.
2. ${}{\overline {-z}}=-{\overline {z}}$.
3. ${}{\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}}$.
4. For ${}z\neq 0$ we have ${}{\overline {1/z}}=1/{\overline {z}}$.
5. ${}{\overline {\overline {z}}}=z$.
6. We have ${}{\overline {z}}=z$ if and only if ${}z\in \mathbb {R}$ holds.

Proof

See exercise.

$\Box$

Lemma

For a complex number

${}z$ the following relations hold.

1. ${}{\overline {z}}=\operatorname {Re} \,{\left(z\right)}-{\mathrm {i} }\operatorname {Im} \,{\left(z\right)}$.
2. ${}\operatorname {Re} \,{\left(z\right)}={\frac {z+{\overline {z}}}{2}}$.
3. ${}\operatorname {Im} \,{\left(z\right)}={\frac {z-{\overline {z}}}{2{\mathrm {i} }}}$.

Proof

See exercise.

$\Box$

The square ${}d^{2}$ of a real number is always nonnegative, and the sum of two nonnegative real numbers is again nonnegative. For a nonnegative real number ${}c$ there exists a unique nonnegative square root ${}{\sqrt {c}}$, see exercise Hence the following definition yields a well-defined real number.

Definition

For a complex number

${}z=a+b{\mathrm {i} }\,,$

the modulus is defined by

${}\vert {z}\vert ={\sqrt {a^{2}+b^{2}}}\,.$

The modulus of a complex number ${}z$ is, due to the Pythagorean theorem, the distance of ${}z$ to the zero point ${}0=(0,0)$. The modulus is a mapping

$\mathbb {C} \longrightarrow \mathbb {R} _{\geq 0},z\longmapsto \vert {z}\vert .$

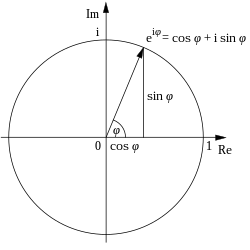
The set of all complex numbers with a certain modulus form a circle with the zero point as center and with the modulus as radius. In particular, all complex numbers with modulus ${}1$ form the complex unit circle. The numbers of the complex unit circle are by the formula of Euler in relation to the complex exponential function and to the trigonometric functions, see fact and fact. We further mention that the product of two complex numbers of the unit circle may be computed by adding the angles starting from the positive real axis counter clockwise.

Lemma

The modulus of complex numbers

fulfils the following properties.

1. ${}\vert {z}\vert ={\sqrt {z\ {\overline {z}}}}$.
2. For real ${}z$ the real and the complex modulus are the same.
3. We have ${}\vert {z}\vert =0$ if and only if ${}z=0$.
4. ${}\vert {z}\vert =\vert {\overline {z}}\vert$.
5. ${}\vert {zw}\vert =\vert {z}\vert \cdot \vert {w}\vert$.
6. For ${}z\neq 0$ we have ${}\vert {1/z}\vert =1/\vert {z}\vert$.
7. ${}\vert {\operatorname {Re} \,{\left(z\right)}}\vert ,\vert {\operatorname {Im} \,{\left(z\right)}}\vert \leq \vert {z}\vert$.
8. ${}\vert {z+w}\vert \leq \vert {z}\vert +\vert {w}\vert$ (triangle inequality).

Proof

We only show the triangle inequality, for the other statements see exercise. Because of (7) we have for every complex number ${}u$ the estimate ${}\operatorname {Re} \,{\left(u\right)}\leq \vert {u}\vert$. Therefore,

${}\operatorname {Re} \,{\left(z{\overline {w}}\right)}\leq \vert {z}\vert \vert {w}\vert \,,$

and hence

${}{\begin{aligned}\vert {z+w}\vert ^{2}&=(z+w){\left({\overline {z}}+{\overline {w}}\right)}\\&=z{\overline {z}}+z{\overline {w}}+w{\overline {z}}+w{\overline {w}}\\&=\vert {z}\vert ^{2}+2\operatorname {Re} \,{\left(z{\overline {w}}\right)}+\vert {w}\vert ^{2}\\&\leq \vert {z}\vert ^{2}+2\vert {z}\vert \vert {w}\vert +\vert {w}\vert ^{2}\\&=(\vert {z}\vert +\vert {w}\vert )^{2}.\end{aligned}}$

By taking the square root, we get the stated estimate.

$\Box$