Complex Analysis/decomposition theorem

Introduction

Using the Cauchy's integral formula, two holomorphic functions, $f_{2}:\mathbb {C} \setminus D_{r}(z_{o})\to \mathbb {C}$ and $f_{1}:D_{R}(z_{o})\to \mathbb {C}$, are defined in the decomposition theorem. These are then utilized for the expansion into a Laurent Series.

Fundamental Definitions

The following fundamental definitions are used in the decomposition theorem:

$K_{r}^{R}(z_{o}):={z\in \mathbb {C} ,:,0\leq r<|z-z_{o}|<R}$

$K_{r}^{\infty }(z_{o}):={z\in \mathbb {C} ,:,0\leq r<|z-z_{o}|}$

$D_{r}(z_{o}):={z\in \mathbb {C} ,:,|z-z_{o}|<r}$

${\overline {D_{r}(z_{o})}}:={z\in \mathbb {C} ,:,|z-z_{o}|\leq r}$

$\gamma _{r,z_{0}}:[0,2\pi ]\to \mathbb {C}$ with $t\mapsto \gamma _{r,z_{0}}(t)=z_{o}+r\cdot e^{it}$

$\int _{\partial D_{r}(z_{o})}f(\xi ),d\xi :=\int _{\gamma _{r,z_{0}}}f(\xi ),d\xi$

Decomposition Theorem for Annular Regions

Let $G\subseteq \mathbb {C}$ be an open set with a holomorphic function on an annular region ${\overline {K_{r}^{R}(z_{o})}}={z\in \mathbb {C} ,:,r\leq |z-z_{o}|\leq R}\subset G$. Then, $f:K_{r}^{R}(z_{o})\to \mathbb {C}$ can be decomposed as $f=f_{1}+f_{2}$ into two holomorphic functions $f_{1}:D_{R}(z_{o})\to \mathbb {C}$ and $f_{2}:K_{r}^{\infty }(z_{o})\to \mathbb {C}$. The decomposition $f=f_{1}+f_{2}$ is unique under the condition $\lim _{z\to \infty }f_{2}(z)=0$.

Proof

The proof considers functions on annular regions centered at $z_{o}=0\in \mathbb {C}$. By suitable composition with a shift, the decomposition theorem can be generalized for arbitrary $K_{r}^{R}(z_{o})={z\in \mathbb {C} ,:,r\leq |z-z_{o}|\leq R}$ with ${\overline {K_{r}^{R}(z_{o})}}\subset G$. Initially, the proof idea for the decomposition theorem is discussed.

Proof Idea

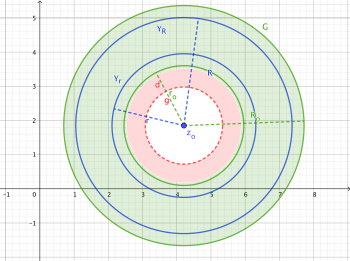
• The center $z_{o}=0\in \mathbb {C}$ of circular rings is a special case that can be used to generalize the statement for arbitrary circular rings $z_{o}\in \mathbb {C}$.
• Definition of a boundary cycle over a circular ring with two integration paths over an outer boundary and an inner boundary with reversed orientation.
• Application of the Cauchy Integral Theorem for cycles.
• Decomposition of the integral over a cycle into two partial integration paths along the inner and outer boundaries.
• One partial integral will provide the principal part of the Laurent expansion, while the other partial integral will yield the remainder of the integral.

Uniqueness of the Decomposition

The decomposition is generally not unique because the constant cannot be uniquely assigned to either the principal part or the remainder. The additional condition for the limit $z\to \infty$ ensures uniqueness, as the constant is then assigned to the remainder.

Proof 1: Circular Rings with Center 0

We consider holomorphic functions on circular rings around the point $z_{o}\in \mathbb {C}$. The point $z_{o}\in \mathbb {C}$ serves as the expansion point of the Laurent series with $(z-z_{o})^{n}$ where $n\in \mathbb {Z}$. Initially, we can restrict to circular rings around 0 (and thus around the expansion point 0), since any function $f:G\to \mathbb {C}$ with $z_{o}\in \mathbb {C}$ and a circular ring ${\overline {K_{r}^{R}(z_{o})}}\subset G$ can be transformed into a function $f_{z_{o}}:G_{z_{o}}\to \mathbb {C}$ with:

$G_{z_{o}}={z-z_{o}\in \mathbb {C} ,:,z\in G}$ and $0\in G_{z_{o}}$, as $z_{o}\in G$.

$f_{z_{o}}:G_{z_{o}}\to \mathbb {C}$ with $f_{z_{o}}(z):=f(z-z_{o})$.

${\overline {K_{r}^{R}(0)}}\subset G_{z_{o}}$ as ${\overline {K_{r}^{R}(z_{o})}}\subset G$.

Proof 2: Definition of the Boundary Cycle for the Circular Ring

We define two integration paths along the inner and outer boundaries of the circular ring. These two paths have opposite orientations.

$\gamma _{1}:[0,2\pi ]\to \mathbb {C}$ with $t\mapsto \gamma _{R,z_{0}}(t)=z_{o}+R\cdot e^{it}$.

$\gamma _{2}:[0,2\pi ]\to \mathbb {C}$ with $t\mapsto \gamma _{r,z_{0}}(t)=z_{o}+r\cdot e^{-it}$.

$\Gamma :=\gamma _{1}+\gamma _{2}$.

Proof 3: Null-Homologous Cycle

Since ${\overline {K_{r}^{R}(z_{o})}}={z\in \mathbb {C} ,:,r\leq |z-z_{o}|\leq R}\subset G$, $\Gamma$ is a null-homologous cycle, as only the inner points of the circular ring have a winding number of 1, and all inner points (including the circular ring’s boundary) belong to $G$.

Proof 4: Application of the Cauchy Integral Formula for Cycles

For $z\in K_{r}^{R}(z_{o})$, the following holds:

$n(\Gamma ,z)\cdot f(z)={\frac {1}{2\pi i}}\int \limits _{\Gamma }{\frac {f(\xi )}{\xi -z}},d\xi ={\frac {1}{2\pi i}}\left(\int \limits _{\gamma _{1}}{\frac {f(\xi )}{\xi -z}},d\xi +\int \limits _{\gamma _{2}}{\frac {f(\xi )}{\xi -z}},d\xi \right)$.

Proof 5: Substitution for Integration Paths

Since $n(\Gamma ,z)=1$ for $z\in K_{r}^{R}(z_{o})$, we get the following by substituting the integration paths:

$f(z)=\underbrace {{\frac {1}{2\pi i}}\int \limits _{\partial D_{R}(z_{o})}{\frac {f(\xi )}{\xi -z}},d\xi } {=f_{1}(z)}+{\bigg (}\underbrace {-{\frac {1}{2\pi i}}\int \limits {\partial D_{r}(z_{o})}{\frac {f(\xi )}{\xi -z}},d\xi } _{=f_{2}(z)}{\bigg )}$

The minus sign before the second integral arises due to the reversed direction of the path $\gamma _{2}$.

Proof 6: Standard Estimation

We consider the limit of the integral $|f_{2}(z)|$ for $z\to \infty$ with $C:=\max \limits _{\xi \in \partial D_{r}(z_{o})}|f(\xi )|$:

$|f_{2}(z)|=\left|-{\frac {1}{2\pi i}}\int \limits _{\partial D_{r}(z_{o})}{\frac {f(\xi )}{\xi -z}},d\xi \right|\leq \int \limits _{\partial D_{r}(z_{o})}\left|{\frac {f(\xi )}{\xi -z}}\right|,d\xi$

$\leq \int \limits _{\partial D_{r}(z_{o})}{\frac {C}{|\xi -z|}},d\xi \leq \underbrace {2\pi r} {L(\gamma _{2})}\cdot \max \limits {\xi \in \partial D_{r}(z_{o})}{\frac {C}{|\xi -z|}}$

Since this is an upper bound and the prefactors are all smaller than 1, they can simply be omitted.

Proof 7: Limit Process for Standard Estimation

Thus, we obtain:

$\lim _{z\to \infty }|f_{2}(z)|\leq \lim _{z\to \infty }\underbrace {2\pi r} {L(\gamma _{2})}\cdot \max \limits {\xi \in \partial D_{r}(z_{o})}{\frac {C}{|\xi -z|}}=0$

Proof 8: Taylor Expansion with Cauchy Kernel

The series expansion occurs with the Cauchy's Integral Theorem for Disks in the red-marked convergence area:

${\begin{aligned}f_{1}(z)&={\frac {1}{2\pi \mathrm {i} }}\oint _{\partial D_{R}(z_{o})}{\frac {f(\zeta )}{\zeta -z}}\mathrm {d} \zeta ={\frac {1}{2\pi \mathrm {i} }}\oint _{\partial D_{R}(z_{o})}{\frac {f(\zeta )}{\zeta -z_{o}-(z-z_{o})}}\mathrm {d} \zeta \\&{=}{\frac {1}{2\pi \mathrm {i} }}\oint _{\partial D_{R}(z_{o})}{\frac {f(\zeta )}{\zeta -z_{o}}}\cdot {\frac {1}{1-{\frac {z-z_{o}}{\zeta -z_{o}}}}}\mathrm {d} \zeta \,\\&{\overset {|{\frac {z-z_{o}}{\zeta -z_{o}}}|<1}{=}}{\frac {1}{2\pi \mathrm {i} }}\oint _{\partial D_{R}(z_{o})}{\frac {f(\zeta )}{\zeta -z_{o}}}\sum _{n=0}^{\infty }\left({\frac {z-z_{o}}{\zeta -z_{o}}}\right)^{n}\mathrm {d} \zeta \\&=\sum _{n=0}^{\infty }\underbrace {\left({\frac {1}{2\pi \mathrm {i} }}\oint _{\partial D_{R}(z_{o})}{\frac {f(\zeta )}{(\zeta -z_{o})^{n+1}}}\mathrm {d} \zeta \right)} _{a_{n}}(z-z_{o})^{n}\end{aligned}}$

(see also Abel's Lemma).

Proof 9: Extension of the Domain to the Interior of the Annulus

The domains of the two functions are currently limited to the annular region. 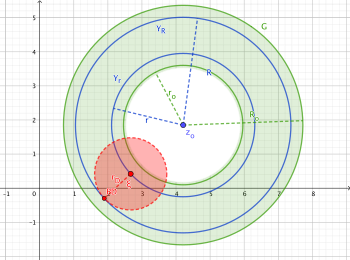We extend the function $f_{1}$ step by step to the interior of the annulus.

Proof 10: Development Point Moves to the Inner Circle

The Taylor expansion moves along a circular path in $K_{r}^{R}(z_{o})$. Using the Cauchy integral formula and the local developability in power series/Taylor series. Thus, we can extend the function using the identity theorem to a region that is the union of the (green-marked) annular region and the (red-marked) open disk. At the same time, the holomorphic criterion is incorporated, which states that a function is holomorphic if it can be locally developed in power series within a region.

Proof 11: Moving Circular Regions as Convergence Region for Power Series

Proof 11: Holomorphic Extension - Disk, Annulus

Using the Identity Theorem, two holomorphic functions agree if they agree on a non-discrete set. In this case, the set is the annular region $G=K_{r_{o}}^{R_{o}}$.

The red annulus represents the extension with all disks and development points on the trace.

Proof 12: Convergence Region of the Power Series

For the integrand $f_{1}$, we can again develop a Taylor series using the Cauchy's Integral Theorem for Disks and the commutability of limit processes. These developments have a disk as the region of convergence, where the series converges for all $z$ inside the disk (see Abel's Lemma). The following figure shows the extension of the domain after applying the identity theorem to the disks as the region of convergence for the Taylor expansion and the intersection with the annular region $K_{r}^{R}(z_{o})$. The intersection is always a non-discrete set, and the holomorphic extension to the union is uniquely determined by the identity theorem.

Proofs 13: Iteratively Extend the Convergence Region

Extend the domain to cover the entire interior of the annulus by continuing the process. Repeatedly apply the identity theorem for the holomorphic extension of 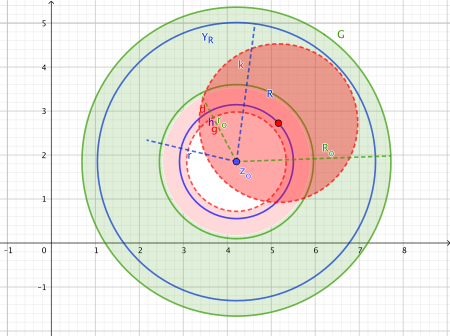$f_{1}$. The development points of the Taylor expansions now lie along a circular integration path with a smaller radius.

Proof 14a: Transformation of Domain for the Main Part

For the main part, we replace the function $f_{2}$ with $h$ using the transformation $T(z):=z_{o}+{\frac {1}{z}}$:

$h(z):=(f_{2}\circ T)(z)=f_{2}\left(T(z)\right)=f_{2}\left(z_{o}+{\frac {1}{z}}\right)$

With this transformation, we have:

$|z|<{\frac {1}{r}},\Longrightarrow |T(z)-z_{o}|>r$

Thus, an analogous approach for $f_{1}$ can also be applied to the extension of $h$. For $h$, the annular region $K_{R_{1}}^{r_{1}}(0)$ with $0<R_{1}:={\frac {1}{R}}<{\frac {1}{r}}=:r_{1}$ is considered. The function $h$ can also be holomorphically extended for $0\in \mathbb {C}$. However, $0\in \mathbb {C}$ is not defined under the transformation $T$ in $\mathbb {C}$. Thus, we can extend $f_{2}$ holomorphically to $K_{r}^{\infty }(z_{o})$.

Proof 14b: Analogous Approach for the Main Part

Analogous to the extension of the annulus from the outer region to the interior, the annulus can also be extended to the exterior by performing the Taylor expansion for the integral $f_{2}$ using the Cauchy Kernel. It should be noted that the development point of the Taylor expansion moves along the path of $\gamma _{R}$, and the region of convergence of the Taylor expansion does not cover the inner path $\gamma _{r}$, as the integral of $f_{2}$ would otherwise not be defined.

See also

• Abel's Lemma

Page Information

You can display this page as Wiki2Reveal slides

Wiki2Reveal

The Wiki2Reveal slides were created for the Complex Analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.

• This page is designed as a PanDocElectron-SLIDE document type.
• Source: Wikiversity https://en.wikiversity.org/wiki/Complex%20Analysis/decomposition%20theorem
• see Wiki2Reveal for the functionality of Wiki2Reveal.

Translation and Version Control

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

• Source: Kurs:Funktionentheorie/Zerlegungssatz - URL:

https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Zerlegungssatz

• Date: 1/2/2025