Complex Analysis/Path Integral

Introduction

This page on the topic Path Integral can be displayed as Wiki2Reveal slides. Individual sections are treated as slides, and changes to the slides are immediately reflected in their content. The following subtopics are covered in detail:

(1) Paths as continuous mappings from an interval $[a,b]$ into the complex numbers $\mathbb {C}$ over which integration is performed,

(2) Derivatives of curves/paths as a prerequisite for the definition of path integrals,

(3) Definition of path integrals.

learning requirements

The learning resource on the topic Path Integral has the following prerequisites, which are helpful or necessary for understanding the subsequent content:

•The concept of a path in a topological space,

•Differentiability in real analysis,

•Integration in real analysis.

Geometric concept of the path integral

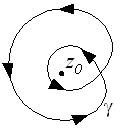
The following curve $\gamma$ encircles a point $z_{0}\in \mathbb {C}$ twice.

Integral over an interval

Let $G\subseteq \mathbb {C}$ be a domain and $g\colon [a,b]\to \mathbb {C}$ a complex-valued function. The function $g$ is called integrable if

\operatorname {Re} (g):G\to \mathbb {R}

and

\operatorname {Im} (g):G\to \mathbb {R}

with

g=\operatorname {Re} (g)+i\cdot \operatorname {Im} (g)

are integrable functions. One defines

\int \limits _{a}^{b}g(x)\mathrm {d} x:=\int \limits _{a}^{b}\operatorname {Re} (g)(x)\mathrm {d} x+\mathrm {i} \int \limits _{a}^{b}\operatorname {Im} (g)(x)\mathrm {d} x

.

Thus, the integral is $\mathbb {C}$ -linear. If $g$ is continuous and $G$ is a primitive of $g$ , then as in the real case,

\int \limits _{a}^{b}g(x)\mathrm {d} x=G(b)-G(a)

.

Extension of the integral concept

The concept of integration is extended to the complex plane by defining an integration path as follows: If $f\colon G\to \mathbb {C}$ is a complex-valued function on a domain $G\subseteq \mathbb {C}$ , and $\gamma \colon [a,b]\to G$ is a piecewise continuously differentiable path in $G$ , the path integral of $f$ along the path $\gamma$ is defined as

\int \limits _{\gamma }f:=\int \limits _{\gamma }f(z),\mathrm {d} z:=\int \limits _{a}^{b}f(\gamma (t))\cdot \gamma '(t),\mathrm {d} t.

The dot here denotes complex multiplication.^[1]

Cauchy Integral Theorem

The central statement about path integrals of complex functions is the Cauchy Integral Theorem: For a holomorphic function $f$ , the path integral depends only on the homotopy class of $\gamma$ off. Is $U$ is simply connected, the integral depends only on the start and endpoints, independent of $\gamma$ .

Analogous to the real case, the length of the path $\gamma :[a,b]\rightarrow \mathbb {C}$ is defined by

\operatorname {L} (\gamma ):=\int \limits _{a}^{b}\left|\gamma '(t)\right|\mathrm {d} t

.

For theoretical purposes, the following inequality, the so-called standard estimate, is of particular interest:

\left|\int _{\gamma }f(z),\mathrm {d} z\right|\leq \operatorname {L} (\gamma )\cdot C

, if

\left|f(z)\right|\leq C

for all

z\in \gamma ([0,1])

.

As in the real case, the path integral is independent of the parametrization of the path $\gamma$ , i.e., it is not necessary to choose $[0,1]$ as the parameter range, as can be shown by substitution. This allows for the definition of complex path integrals by replacing the path $\gamma$ with a curve ${\mathcal {C}}$ in $\mathbb {C}$ .

Tasks

Let $\gamma \colon [a,b]\to G$ with $t\mapsto \gamma (t)=\sin(t)+i\cdot t^{2}$ . Determine $\gamma '(t)$ !

Compute the path integral $\int \limits _{\gamma }{\frac {1}{z}},\mathrm {d} z$ for the path $\gamma \colon [0,2\pi ]\to \mathbb {C}$ with $t\mapsto \gamma (t)=r\cdot e^{i\cdot t}$ .

Calculate the length of the path $L(\gamma )$ with $t\mapsto \gamma (t)=r\cdot e^{i\cdot t}$ .