Complex Analysis/Curves
Introduction
[edit | edit source]In the Mathematics a curve (of lat. curvus for "bent", "curved") is a one dimensionals object in a two-dimensional plane (i.e. a curve in the plane) or in a higher-dimensional space.
Parameter representations
[edit | edit source]- Multidimensional analysis: A continuous mapping is a curve in the .
- Complex Analysis: Continuous mapping is a path in (see also path for integration).
Explanatory notes
[edit | edit source]A curve/a way is a mapping. It is necessary to distinguish the track of the path or the image of a path from the mapping graph. A path is a steady mapping of a interval in the space considered (e.g. or ).
Example 1 - Plot
[edit | edit source]Example 1 Curve as a solution of an algebraic equation
[edit | edit source]|
resp. . Determine for the curve all with |
Examples 2
[edit | edit source]The mapping
describes the Unit circle in the plane .
describes the Unit circle in the Gaussian number level .
Examples 3
[edit | edit source]The mapping
describes a curve with a simple double point at , corresponding to the parameter values and .
Direction
[edit | edit source]As a result of the parameter representation, the curve receives a directional direction in the direction of increasing parameter.[1][2]
Curve as Image of Path
[edit | edit source]Let or be a path. is the image of a path
- .
Difference - Graph und Curve
[edit | edit source]For a curve the Supr or curve is a subset of , while the graph of function is.
Task - Plot Graph und Curve
[edit | edit source]use CAS4Wiki :
Animation of the track
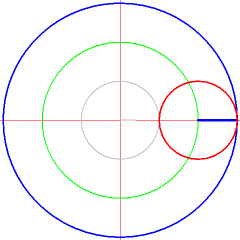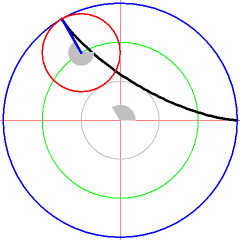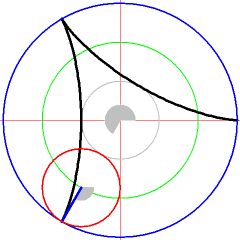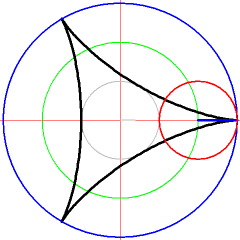
[edit | edit source]Curves in Geogebra
[edit | edit source]First create a slider for the variable and two points or and generate with the sum of both location vectors of and . Analyze the parameterization of the curves.
Geogebra - Interactive Implementation
[edit | edit source]Create a value slider in Geogebra with the variable name and create the following 3 points step by step in the command line of Geogebra and move the value slider for after that.
K_1:(2*cos(t),2 * sin(t))
K_2:(cos(3*t),sin(3*t))
K: K_1+K_2
The construction about will create an interactive representation of the the follow path . Observe the point in Geogebra.
See also interaktive Example in Geogebra
Representations of Image Sets by Equations
[edit | edit source]A curve can also be described by one or more equations in the coordinates. The solution of the equations represents the curve:
- The equation describes the unit circle in the plane.
- The equation describes the curve indicated above in parameter representation with double point.
If the equation is given by a Polynomial, the curve is called algebraic.
Graph of a function
[edit | edit source]Functiongraphs are a special case of the two forms indicated above: The graph of a function
can be either as a parameter representation or as equation , wherein the solution quantity of the equation represents the curve by . If theMathematics education of Curve sketching is spoken, this special case is usually only said.
Closed curves
[edit | edit source]Closed curves are continuous mappings with . In the function theory, we need curves in , which can be continuously differentiated. These are called integration paths.
Number of circulations in the complex numbers
[edit | edit source]Smooth closed curves can be assigned a further number, thenumber of revolutions, which curve is parameterized according to the arc curve by
is given. The circulation theorem analogously to a curve in , states that a simple closed curve has the number of revolutions or .
Curves as Independent Objects
[edit | edit source]Curves without an ambient space are relatively uninteresting in w:en:Differential Geometry because every one-dimensional manifold is diffeomorphic to the real line or to the unit circle . Also, properties like the curvature of a curve are intrinsically undetectable.
In algebraic geometry and, correspondingly, in complex analysis, "curves" typically refer to one-dimensional complex manifolds, often also called Riemann surfaces. These curves are independent objects of study, with the most prominent example being elliptic curves. See curve (algebraic geometry)
Historical
[edit | edit source]The first book of Elements by Euclid began with the definition:
- "A point is that which has no parts. A curve is a length without breadth."
This definition can no longer be upheld today because, for example, there are Peano curves, i.e., continuous surjective mappings that fill the entire plane . On the other hand, the Sard's Lemma implies that every differentiable curve has zero area, i.e., as Euclid demanded, it truly has no breadth.
Interactive Representations of Curves in GeoGebra
[edit | edit source]- Tangent vector of a curve in for a curve with tangent vector
- Rolling curves Bicycle reflectors as an example of curves - Cycloid
See also
[edit | edit source]- Space curves in
Literature
[edit | edit source]- Ethan D. Bloch: A First Course in Geometric Topology and Differential Geometry. Birkhäuser, Boston 1997.
- Wilhelm Klingenberg: A Course in Differential Geometry. Springer, New York 1978.
References
[edit | edit source]- ↑ H. Neunzert, W.G. Eschmann, A. Blickensdörfer-Ehlers, K. Schelkes: Analysis 2: Mit einer Einführung in die Vektor- und Matrizenrechnung. Ein Lehr- und Arbeitsbuch. 2. Auflage. Springer, 2013, lSBN 978-3-642-97840-1, 23.5
- ↑ H. Wörle, H.-J. Rumpf, J. Erven: Taschenbuch der Mathematics. 12. Auflage. Walter de Gruyter, 1994, lSBN 978-3-486-78544-9
External Links
[edit | edit source]| Look up Kurve in Wiktionary, the free dictionary. |
Page Information
[edit | edit source]You can display this page as Wiki2Reveal slides
Wiki2Reveal
[edit | edit source]TheWiki2Reveal slides were created for the Complex Analysis' and the Link for the Wiki2Reveal Slides was created with the link generator.
- This page is designed as a PanDocElectron-SLIDE document type.
Translation and Version Control
[edit | edit source]This page was translated based on the following [https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Kurven Wikiversity source page] and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:
- Source: Kurs:Funktionentheorie/Kurven - URL:
https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/kurven
- Date: 12/17/2024

![{\textstyle f:[a,b]\to \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/763b5d67b3caa0202cbb12b11888b3fada72177d)

![{\textstyle f:[a,b]\to \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e72280a43e2f535eeda2b5912ab528f4232a6882)

















![{\textstyle \gamma :[a,b]\to \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd86867849f4e02523af68a9f9651aa09f8d11ec)
![{\textstyle \gamma :[a,b]\to \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b0cee3b566e3c1483861186e732dff553ed4502)

![{\displaystyle \gamma :[a,b]\to \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1d326a550ef41246054e0311de07e1375d535f3)


![{\displaystyle {\begin{array}{rrcl}\gamma :&[0,6\pi ]&\rightarrow &\mathbb {R} ^{2}\\&t&\mapsto &\gamma (t)=\left(3\cdot \cos(t),\sin(t)\right)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7f9e5e15461170a62af8eb626ff2013e4ef6bea)
![{\textstyle t\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f42247447f5ca9e59b3156bf23c61b38cf4bfda9)















![{\textstyle \gamma \colon [a,b]\to \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9f04ae33a56639172b31e1f20a8e5b5da88a79b)








![{\displaystyle \gamma ':[a,b]\to \mathbb {R} ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4985098cd3850bb2c8aa01b67e46fb0e4541a464)
