Calculating the square root of a
In this learning project, we learn how to approximate the square root of a number numerically.
Newton's method
[edit | edit source]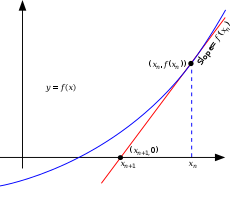
Newton's method is a basic method in numerical approximations. The idea of Newton's method is to "follow the tangent line" to try to get a better approximation. For more details, see w:Newton's method
Try your hand on Newton's method
[edit | edit source]Step-by-step
[edit | edit source]Cut and paste the following wikitext into the sandbox, and enter your favourite number and a first (non-zero!) approximation of its square root. See what happen after multiple edit-and-saves:
{{subst:square root|number|first approximation}}
Sandbox
[edit | edit source]{{subst:square root|17|4.1231056256177}}
4.1231056256177
4.1231056256177
4.1231056256177
4.1231056256177
4.1231056256177
4.1231056256177
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310562562
4.12310877528
4.1282051282
4.33333333333
3
What is going on
[edit | edit source]Our calculator-template {{square root}} implements the formula , which is an instant of the general formula for Newton's method in the case when the function f(x) is given by . It solves the equation numerically, by successive approximations.




