COVID-19/Mathematical Modelling/DiMoT

Disease Modelling Time span (DiMoT) is a set as a domain of functions for which the development of the disease is mathematically described. Functions describe specific properties.

Introductory Example

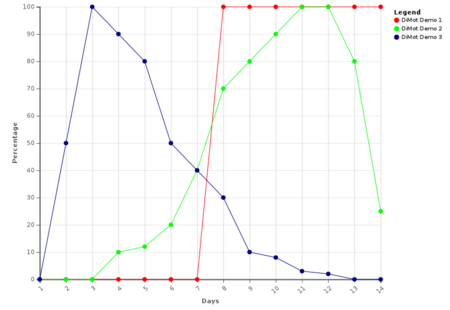
As an introductory example, we assume that the disease modelling period is 14 days. In this disease modeling period, a function should be created to represent the infectivity over this 14-day period. The function should be 100 if 100% of the infected patients are themselves infectious at this time.

In this introductory example the percentage of infected persons are represented by 3 different functions with different developments in time. The curves are fictitious and are only intended to illustrate the principle of disease modelling time spans.

• The red curve shows a temporal development in which people cannot infect others for the first 7 days and after that 7 days 100% of them are able to infect other susceptible citizens for the next 7 days. The disease modelling time span is 14 days.
• in the blue curve 100% of all infected citizens are infectious on the 3 day after infection, after the third day less and less infected persons become infectious for others. This is another function describing a different temporal development with the same DiMoT of 14 days.
• in the green curve the percentage of infected persons increases to 100% on the 11th day and after one day the percentage of infected patients decreases.

Definition: DiMoT

A Disease Modelling Time span (DiMoT) can defined as

• continuous DiMoT by an Intervall $T:=[a,b]\subset \mathbb {R}$
• discrete DiMoT as a finite set of real values $T\subset \mathbb {R}$ with $|T|=n\in \mathbb {N}$.

Example

A Disease Modelling Time span (DiMoT) for the example above is in

• continuous DiMoT case the intervall $T:=[0,14]\subset \mathbb {R}$ or as
• discrete DiMoT the finite set of real values $T=\{1,2,...,14\}\subset \mathbb {R}$ with $|T|=14\in \mathbb {N}$.

Learning Tasks

Latency Geogebra interactive example of trigonometric function.

• Hospitalisation and mortality show a delay in the increase and decrease of numbers. Explore the concept of Latency and explain how the latency can be visualized with graphs. What is the difference and what are the similarities between just a latency of a signal and a dependency and delay of hospitalization and mortality. If a signal delay can be identified, explain how preparedness for response can take that into account if latency provides sufficient response time for Risk Management.

Probability Density and Report Time of Cases

Now we use the DiMoT as the domain of a probability density over an interval an extend the DiMoT interval to the negative numbers. This example shows a probabilty density for the reported time stamp of cases and the (estimated?) time stamp of the infection of the patient. The reporting time can be regarded as a date that is documented in the database e.g. of a public health agency. The point in time when a patient was infected can be a very fuzzy information with assumption of events that might expose the patient to other COVID-19 positive citizens (which might not know that they were infectious at that time). Neverthess some information can be gathered to identify the time of infection and the appearance of first symptoms and the time and date when the test was performed. Assume we create a probabilty density on the negative numbers that show number of reported case and the delay from the time of infection and the time of reporting the positive case. We start with the absolute numbers.

• Assume a reported case at day 0 was infected 13 days before and we define a discrete probabilty distribution on the negative integer numbers, then we assign a +1 to -13.
• if we have 10 reported cases that are (probably) infected 13 days before their case was reportedm then we assign a +10 to -13.
• we apply that for other times spans between reporting time and infection time.
• if the infection time can be roughly determined between 11th,12th or 13th day before the reporting time, then we assign $+{\frac {1}{3}}$ to -11,-12 and -13 for a specific case.
• the following curves show different examples for values - these values a not real values. The should illustrate the basic principles for functions on the DiMoT set as domain.

Graph with absolute Number of Cases

The following graph are demo numbers to show the process from creating a discrete probability distribution from a given number of cases. Assume for this chart we could ask COVID-19 positive patients at which event they might are infected.

Absolute Number and Probabilty Distribution

Day	Infected - Count	Probability Density
-13	1	0,0102040816326531
-12	18	0,183673469387755
-11	15	0,153061224489796
-10	34	0,346938775510204
-9	12	0,122448979591837
-8	7	0,0714285714285714
-7	9	0,0918367346938776
-6	2	0,0204081632653061
-5	0	0
-4	0	0
-3	0	0
-2	0	0
-1	0	0
0	0	0

From Graph for the Number of Cases towards a Probability Density

Absolute numbers as example for a Disease Modelling Time

Probability density as example for a Disease Modelling Time

We sum up all cases for data collection 1, 2 and 3 (3 graph with the cases above). We devide each absolute number by sum in the respective column and calculate the Empirical Probability. The following chart is generated with CSV2Chart from the CSV file in the respository on GitHub.

Discrete Probability Distribution

Discrete probability distribution (e.g. on the 14 days) can be calculated on the DiMoT by dividing the absolute numbers on that day by the total numbers of patients for which the infection day can be determined prior to the detection day of the case in the health system. The second graph shows a continuous probability density derived from the discrete probability distribution.

Continuous Probability Distribution

Analyze the possible mathematical methods to estimated a continuous probability distribution from a set of discrete data of cases. Identify mathematical methods to describe a kind of quality for the estimation.

Convolution

• What is a convolution of two functions and how can the convolution with a density function be used to create a graph that shows the distribution of infections times rather than the density functions of infections for the registration time of a case in the public health system?
• The convolution shifts the graph to left on the x-axis and creates a smooth operation on the source graph. Explain why the continuous density function performs the transformation of the source graph. Perform a discrete and continuous convolution as a learning task (e.g. in LibreOffice Calc, GNU Octave, R, NumPy, ...

See also

• Convolution of Functions
• CSV2Chart create chart from CSV files with an AppLSAC
• LibreOffice Calc
• GNU Octave
• R
• NumPy