Beat (acoustics)

Fig. 1 Beats in amplitude between two sinusoidals with nearly the same frequency. The beat frequency is $f_{B}=1/\Delta t.$ Also shown is ${\bar {\omega }}=2\pi {\bar {f}}$, where ${\bar {f}}$ is the average of the two frequencies.

Fig. 2 Small coprime integer pairs.

Fig. 3 Played above a piano's C, the notes and frequency ratios are corresponding notes are: (6/5, 5/4, 4/3, 3/2, 8/5, 5/3) and (E♭, E, F, G, A♭, A), respectively.

Fig. 4 Overtones are associated with the harmonics of a guitar or violin string

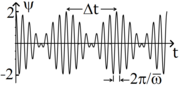
The sum of two sinusoidal waves with equal amplitude and nearly equal frequency is shown in figure 1: The time interval, $\Delta t,$ defines the beat frequency $f_{B}$ through the equation, $f_{B}\Delta t=1$. For two waves of nearly the same frequency, the beat frequency is:

$f_{B}=|\Delta f|=|f_{2}-f_{1}|.$              (Eq. 1)

• For more information, visit the Wikipedia article, Beat (acoustics).

Beats also occur when the frequencies are not nearly equal, but instead have a ratio that is close to $p/q,$ where $q$ and $q$ are relatively small coprime integers with $2>p>q>1,$ as shown in figure 2. The figure is inspired by a proof of the countability of rational numbers. Ratios that are not coprime are shown in red, and smaller integers occupy the upper left hand corner. In music these ratios are associated with intervals that are just. Figure 2 suggests that after the the unison (1/1) and octave (2/1), the third most fundamental ratio is the perfect fifth, with a (3/2) ratio. For example, 300 Hz and 200 Hz create a just perfect fifth (P5) that is exactly tuned. Slight modification from an exactly tuned interval is called detuning, and this detuning can cause beats. As discussed below, under certain circumstances, these beats can be understood using the mechanism described in figure 1, where (amplitude) beats are caused by two harmonics of nearly matching frequencies. But this simple explanation does not seem sufficient for all cases where beats are heard between two pitches that are slightly detuned from the just $(p/q)$ ratio.

Musicians will recognize these frequency ratios in figure 3 as notes played against middle C. The figure demonstrates the impossibility of fitting the piano's 12-tone scale to these intervals. A whole tone above C is D, and that ratio cannot be uniquely defined using just intonation: If you go up a just fifth and down a just fourth, the D-to-C frequency ratio should be 9/8. But going up a sixth and down a fifth yields a different ratio, namely 10/9.

Not shown in the figure 3 are some fascinating just ratios involving seven: Two nearly equal ratios, $7/5\approx 10/7$ create flattened and sharpened versions of the tritone (from C to G♯), an interval often considered to be dissonant. On the other hand, the $7/4$ ratio is a flattened version of the diminished seventh, which is associated with the harmonic seventh and the ratio 4:5:6:7. When sung or played by a skilled quartet capable of flattening that top note, this is one of music's most consonant chords.

Amplitude beats among harmonics

• For more information about this section, see Beat (acoustics)/Amplitude beats

These are caused by matching harmonics just interval defined by the ratio $p/q$ of coprime integers. If the detuned frequencies are $pf_{0}+\Delta f_{p}$ and $qf_{0}+\Delta f_{p}$, then the beat frequency between the $iq^{\text{th}}$ harmonic of $f_{p}$, and the $ip^{\text{th}}$ harmonic of $f_{q}$ is:

$f_{i}^{H}=i\cdot \left|q\Delta f_{p}-p\Delta f_{q}\right|\equiv {\frac {1}{T_{i}^{H}}}\,,$              (Eq. 2a)

where $i$ is a positive integer. Here the superscript "H" can refer either to "harmonic" or "Helmholtz", since Helmholtz proposed a relationship between these beats and the consonance of just intervals in 1877.

Hearing the beats

The OGG and WAV files in Table 1 play clicks at 90 beats per minute and are arranged in 3/4 time:

1. Four bars with no metronome: Listen for the beats
2. Four bars with metronome on the first beat. Listen: 1-2-3 | 2-2-3 | 3-2-3 | 4-2-3
3. Four bars with no metronome. Count: rest-2-3 | 2-2-3 | 3-2-3 | 4-2-3
4. One bar with metronome. Listen: click-2-3

Table 1

interval	Frequencies	ogg file	wav file
Fifth	300.0-200.25
Maj 6th	333.333-200.3
Fourth	266.667-200.188
Maj 3rd	250.0-200.15
min 6th	320.0-200.094
min 3rd	240.0-200.125
Tritone	280.0-200.214

The challenge occurs at step 3: Try to count the beats as if they were a four measure rest in a waltz. If you are the clicker, you would come on the first beat of the fifth bar after that rest. After a while you might be able to start counting at the beginning. If you are a musician, think of the clicks as a percussionist who has four bars of rest, four bars of clicks, four bars of rest, and one bar of clicks.

The 3-count "waltz" rhythm was deliberately chosen because there apparent mechanism by which the downbeat "1", should differ from "2" and "3". But lack of an apparent mechanism does not imply absence of a mechanism. In later section we shall learn that process by which the brain interprets sound is quite bewildering. I certainly do hear a downbeat that differs from "2" and "3", probably because I am thinking "waltz" when I hear it. Also, it was necessary for me to listen to a sound file up to a dozen times before I felt comfortable hearing the beats. Perhaps I was just learning the rhythm so that I could correctly time the "rests". This flaw in experimental design could be resolved by a blind study that randomly changes the beat frequency over time (by introducing a slow variation in one or both frequencies.)

The OGG files are compressed, which means they are not guaranteed to be exact duplications of two sinusoidal waves. But OGG are often easier to access than WAV files. If you can hear the difference between the two versions, it is almost certainly because the OGG file's compression has modified the wave from it's original form, which was a sum of two sine waves:

$A_{1}\sin(\omega _{1}t)+A_{2}\sin(\omega _{2}t)\,,$

where in our example $A_{1}=A_{2},$ and omega, $\omega =2\pi f,$ is called angular frequency.

It is important to know that the OGG and WAV sound files shown above were produced as pure tones, i.e., sinusoidal waves without overtones. We cannot guarantee that some process adds overtones to the signal. Without overtones, we cannot apply our formula for amplitude beats among harmonics. Since OGG files are compressed, we cannot exclude the possibility that these OGG files contain overtones. But any non-linear processes can create overtones.

Phase beats

Fig. 5: Harmonic (top) and inharmonic (bottom) signals

The same formula used to define amplitude beats in the previous section can be used to describe what we shall call "phase beats". One distinction is that the integer $i$ takes on only two the integers $(1,2.)$

$f_{i}^{\phi }=i\cdot \left|q\Delta f_{p}-p\Delta f_{q}\right|\equiv {\frac {1}{T_{i}^{H}}}$              (Eq. 2b)

Equations 2a and 2b differ only in the use of the superscript $\phi$ to denote "phase".

Phase beats are closely related to inharmonicity, which is known to give percussive instruments a distinctively dissonant sound. A dissonant inharmonic signal is shown in blue as the bottom graph in in figure 5. The top graph (red) in the same figure shows a harmonic signal because three angular frequencies follow the harmonic series: $\sin \omega t,$ with $\omega =(1,2,3),$ while the bottom (inharmonic) signal uses $\omega =(1,2,3.1).$ This inharmonic signal corresponds exactly to three tones, with the lowest two being an octave, accompanied by a top tone that is a detuned fifth $(3.1/2\approx 3/2)$ above the middle tone. Each signal in figure 5 has a duration of approximately 7 cycles of the fundamental, and the inharmonic signal is characterized by an evolution of the shape of one cycle over time. This same evolution of shape can also be seen in figure 6 below.

Fig. 6. A just fifth, detuned by adding signals of 300 Hz and 200.5 Hz. The centers of the shaded regions A and C are separated by one period of ${}^{1}\!T_{B}^{\phi }$. The $i=2$ beat period separates B from A or C. The signal at B is the additive inverse of the signals at A and C because the ratio (3/2) contains an even number.

Fig. 8: Detuned sequence that converges to a just fifth (3/2 ratio.)

Figure 6 shows the sum of two pure tones spanning slightly over one beat period of the $i=1$ beat. If humans perceive the inverse of a pattern exactly the same as the pattern itself, then the AB transition will sound exactly like the BC transition, causing the $i=1$ to be nothing more than two beats of $i=2$, rendering the $i=1$ be effectively nonexistent.

The following equations describe a just interval that is exactly tuned, where $(p=3,q=2),$ are two relatively prime integers, as shown in figure 7 (below and to the left.)

${\begin{aligned}1<&\,p/q<2\\pqf_{0}=f_{x}&\leftrightarrow T_{0}=pqT_{x}\\f_{p}=pf_{0}&\leftrightarrow T_{p}=qT_{x}\\f_{q}=qf_{0}&\leftrightarrow T_{q}=pT_{x}\\\end{aligned}}$

Fig. 7: $T_{0}$$>T_{q}$$>T_{p}$$>T_{x}$

Table 2

$n$	${\frac {T_{B}}{T_{x}}}$	$P$	$Q$	${\frac {P}{Q}}$	${\text{cents}}$
---	6	3	2	1.500	0.0
1	9	4	3	1.333	203.9
2	15	7	5	1.400	119.4
3	21	10	7	1.429	84.5
4	27	13	9	1.444	65.3
5	33	16	11	1.455	53.3
10	63	31	21	1.476	27.7
50	303	151	101	1.495	5.7
100	603	301	201	1.498	2.9
200	1203	601	401	1.499	1.4
300	1803	901	601	1.499	1.0

A sequence of detuned fifths

Phase beats can be understood by creating a sequence of detuned intervals with frequency ratios that converge to the desired limit. Table 2 (below, left) displays this sequence, starting with the 4/3 ratio at the row labeled n = 1, which is whole tone off from the desired 3/2 ratio. But by the time the sequence reaches 301/201, the detuning is reduced to 2.9 cents.

A graphical construction of this sequence up to P/Q=34/23 is displayed in figure 8 to the right. The cosine wave has been replaced by a triangular wave in order make it easier to see when the maxima of the p-wave and q-wave are perfectly aligned. Each column depicts a musical interval, with the p-wave shown in black and the q-wave in orange. Time flows in the downward direction, and is best measured an a sort of base-6 by mixing multiples of, $T_{0}=6T_{x}$ with multiples of $T_{x}.$ The alignment of the two peaks in the first column at multiples of $T_{0}$ informs us that this is an exactly tuned (3/2) just fifth.

The first member of our sequence is the 4/3 ratio. It can be constructed by first referring to the 3/2 column and noting the p-wave (black) peak at $3T_{0}+2T_{x},$, which is four p-wave periods from the $t=0$ peak at the top. Now imagine that you "stretch" this p-wave segment by an amount equal to $T_{x}$ so that the peak is now at $3T_{0}+3T_{x},$ which is also the location of the (unstretched) q-wave. A red line and arrow from $3T_{0}+2T_{x}$ in the 3/2 column to 4/3 shows this transition. The reader can verify by counting the peaks that $3T_{0}+3T_{x}$ is the period of a just interval with three cycles of the q-wave and 4 cycles of the p-wave. There is no need to plot the 4/3 column beyond its period (4/3) because the pattern just repeats itself forever.

An exactly tuned just fifth has a 3/2 frequency ratio. Each member of the sequence, $(4/3,$ $7/5,$ $10/7,$ $\ldots$$P_{n}/Q_{n}$ $\ldots )$ is also a just interval, with a periodicity equal to $(6n+3)T_{x}.$ Using a method called mathematical induction, it can be shown that this periodicity is the beat period, $T_{1}^{\phi }$ associated with equation 2 for $i=1$ phase beats.

The presumption is that we can use this series of intervals as a model for any detuned just intervals  • For more information, visit Beat_(acoustics)/Exact_phase_beats.

The symmetry "paradox"

The postulate is that we can use this sequence to understand all detuned just intervals. The premise for this postulate that intervals seem to vary continuously as the frequency ratio changes. But one property of intervals defined by ratios that are rational numbers presents us with a puzzle that needs to be resolved. The periodicity of the $7/5$ interval is $2T_{0}+3T_{x},$ and half that value is at $t=T_{0}+1.5T_{x}.$ From figure 8, we can see that the peaks of the p and q waves are aligned, but in the negative direction. But the adjacent $10/7$ interval exhibits a different pattern midway through its periodicity of $3T_{0}+3T_{x}.$ At $t=T_{0}+4.5T_{x},$ the peaks are aligned, but in opposite directions. The midpoints between positive alignments are always aligned, but the nature of that alignment alternates, with the peaks pointing in opposite directions if and only if $P_{n}$ is an odd number.

To resolve this paradox, note that these kinds of beats are not perceived as abrupt "clicks", but an evolution of the sound that repeats itself over a length of time that is long if the interval is almost exactly at just intonation. This can be seen from figure 6, where $3000/2005$ represent an interval that differs from $3/2$ by about 2.4 cents. This gradual evolution of the pattern over time can be seen in figure A. The regions of areas A, B, and C in that figure each have a length of $2T_{0}.$ Just outside those shaded regions shaded areas of A, B, and C are nearly identical pattern inside the shaded regions of the figure 6. The last two intervals in figure 8 display a hint of this phenomenon. Regions of length $2T_{0}$ and $3T_{0}$ are marked in the columns 31/21 and 34/23, respectively.

Biological synchronization

Fig. 9

Fig. 10:

Fig. 11:Neural oscillations

Fig. 12: Fingers move in phase (top) and with opposite phase (bottom)

Fig. 13:

Fig. 14:

Fig. 15: Neuron action potential. (1) Click image to expand, and click here to see a video on this process.

Converting sound waves to nerve impulses

Air is made of molecules so numerous and moving so fast that it can be modeled as a fluid, which stores energy in the form of compression, heat, and bulk motion. Sound transports energy in all three of these forms, setting your eardrum, small bones in your inner ear, and finally nerves in your cochlea into motion, as shown in figures 9 and 10.

• See also: File:Journey of Sound to the Brain.ogv and w:Auditory cortex

Figure 6 accurately describes the pressure inside the ear canal if the source of the sound is the sum of two sinusoidal waves. But what the 30,000 nerve fibers in the auditory nerve send to a variety of locations in the brain is apparently poorly understood. But we can safely rule out the possibility that any part of the brain would process an air pressure versus time graphs such as shown in figure 6. One justificaction for this assertion is that neural oscillation with the highest frequency oscillate at about 140 Hz. And from Tramo (2005): "simple temporal codes for pitch capable of accounting for pitches higher than a few hundred hertz have not been found in the auditory cortex." To borrow from J. B. S. Haldane's comment about the universe, how the brain processes sound is not only stranger than you imagine, but stranger than you can imagine.

Biological synchronization

In addition to transmitting signals to other parts of the brain, neurons can modify the rules which neighboring neurons operate in a process some call neuromodulation, which plays a role in biological synchronization. Figure 12 depicts biological synchronization among motor nerves that govern the fingers of your left and right hands. Nerves transmitting decisions to move fingers in both hands "help" each other stay synchronized as you rapidly move the fingers in an up/down motion. But this coordination is easy only if the fingers move in phase ("up" together and "down" together) as shown in the top portion of figure 12. Perhaps my mind is playing tricks on me, but when performing this activity, I feel as if my right hand is "telling" the left hand what to do. I find it extremely difficult to perform this action quickly if I attempt to move the fingers with opposite phase ("up" with one hand while "down" with the other.)

Analogies versus models

The discussion at figure 12 was an analogy, among other reasons, because motor nerves are involved. Analogies are useful for explaining, and occasionally for inspiring lines of investigation. Figure 13 is another analogy that involves the fact that it is possible for two metronomes become synchronized due to their contact with a freely moving platform. If the metronomes are set to slightly different frequencies, they have been observed to lock into synchronous motion, usually in phase and at a frequency midway between the two individually set frequencies.

Appendix

Beat (acoustics)   /Phase beats   /Literature search   /Just fifth displace stretch   /Exact phase beats   /Differential equations   subpages   drafts  

Under construction

can interact via the fact that they analogy to the finger motion shown in figure 11. A valuable aspect of this analogy is that both systems are modeled by ordinary differential equations that are nonlinear. They weakly interact via the fact that they are resting on the same movable platform, and We have already established that different sets of auditory nerves are responsible for tracking the oscillations of the p and q waves that were discussed above #Phase beats. The theory of biological synchronization in musical harmony is that when pitches of the two waves are slightly detuned, neuromodulation among the two sets of nerves that process each pitch removes the detuning by creating a signal consistent with two pitches tuned exactly to the ratio $p/q.$ At first glance, neuromodulation to effectively modify the frequency of a perceived pitch might seem both unnecessary and impossible. Before creating a spring clock so accurate that permitted a useful measurement of longitude in 1762, John Harrison created pendulum clocks that he claimed were accurate to less than one second per day, even if they operated in adjacent rooms kept at strikingly different temperatures. To appreciate such precision using technology familiar to Isaac Newton, this is equivalent to establishing the length of a 1-meter simple pendulum to within 0.023 millimeters. Frequency is easy to measure to high precision because two different reference signals can be compared with each other. In principle, Harrison should have listened to each beat of the clock to ensure that no clock "skipped" a beat, but casually observing the two clocks several times through the night would have made for a convincing demonstration....Direct quote from Fairfax House: Thus, to ensure that the temperature compensation system worked accurately. In the metronome analogy of figure G, the metronomes are modified by the motion of the base. But the theory of biological synchronization, the neurons that observe the cycles one frequency of the musical interval influence how the neurons count the cycles created by the musical interval's other frequency. other frequency How and why would the brain listen the 440 cycles of concert-A in one second and "miss" a cycle? The phase locking of figure G was not obtained by changing the perceived frequency of the metronome, but by using a rocking motion to change the metronome's actual frequency. Precise measurements of frequency play an important role in physical measurements. Calculation: dt/t=1/60/60/24=1.16E-5 T=sqrt(L/g) dT/T=.5*dL/L if L=1 dL=2.32E-5=0.023mm w:John Harrison John Harrison (3 April [O.S. 24 March] 1693 – 24 March 1776) was a self-educated English carpenter and clockmaker who invented the marine chronometer, a long-sought-after device for solving the problem of calculating longitude while at sea. NEWTON: 25 December 1642 – 20 March 1726/27 The firings are phase locked to the wave, but are separated by a random integer number of periods of the wave. If nerves interact in a way that establishes that two tones have a nearly just frequency ratio, why would nerves take that extra step and "trick" the brain into perceiving the ratio to be exact? In biology, "why" is an evolutionary question. The brain simplifies a vast amount of disorganized information from the senses and converts it into a relatively small amount of instructions to muscles. The creatures that evolved into mammals didn't think (very much.) A decision to flee a predator is best done when the primary instruction is to all legs to act simultaneously. w:Neuroscience of music brief description of non-experts and sequential notes ("tunes") for more information: "Humans with musical absolute pitch do not have better pitch height judgments than those without musical absolute pitch"cccc w:Event-related potential and w:Electroencephalography need to sort out Tutorial 1:The leaky integrate-and-fire neuron model Video available at https://youtube.com/watch?v=rSExvwCVRYg Coombes and Lord ) ... rhythmic motor behavior... w:Hodgkin–Huxley model (4 nonlinear odes). Tadpole quote: "For example, in the mollusc Tritonia and the tadpole Xenopus the escape swim behavior is generated in this fashion ... The study of coupled oscillators has applications in understanding CPG (central pattern generators) neuronal circuits ... " Three of the 41 citing articles involve music: Fletcher: Mode locking in musical instruments https://newt.phys.unsw.edu.au/music/people/publications/Fletcher1978.pdf Metronome synchronization AJP Pantaleone http://salt.uaa.alaska.edu/physics_public/metro.pdf Hodgkin-Husley equations MIT thesis http://web.mit.edu/mcraegroup/wwwfiles/ChuangChuang/thesis_files/Appendix%20C_Hodgkin-Huxley%20Equations.pdf Devil's staircase in gait force profiles