WikiJournal of Science/A card game for Bell's theorem and its loopholes/Tube entanglement
Subpages: The car and the goats Impossible correlations Tube entanglement





It is frustrating that the theory of an entangled system requires knowledge is not usually acquired in a first-semester introduction to quantum mechanics or modern physics. The most elementary entangled system studied in Bell test experiments involve half-spin particles, which clashes with the fact that students are exposed to photon polarization at a much younger age. Photons must be modeled by a far more advanced quantum field theory.
So instead, imagine two cups, one containing coffee and the other tea, and you don't know which is which. Both liquids are sloshing in a circular fashion, in opposite directions, and you don't know which is rotating in which direction. This is not quantum entanglement because the fluids in each cup are macroscopic entities, subject to fluid equations that follow classical Newtonian physics.
Now imagine that each cup is very very small and contains contains only one "atom" of coffee or tea, and each "atom" is near a ground state. In two-dimensions, the lowest three states resemble the vibrational modes of a circular membrane shown to the right. Following the conventions of atomic physics, we have labeled them as the 1s, 2p, and 2s states. We shall construct our entanglement from two "degenerate" 2p states, one shown in the figure, and the other with it's node perpendicular to that shown. And, we shall show how a primitive thought experiment allows one to make a polarizing filter for this system.
Polarization and Malus's law
[edit | edit source]-
Picket fence
-
Two filters
-
Vector component
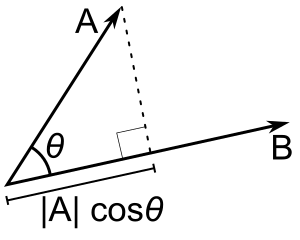
Malus's law is explained at w:special:permalink/838616355#Malus's_law_and_other_properties. The first image above is a photograph of a spinning (circularly polarized) stretched string that is polarized by passing it through a slit. It illustrates the well-known picket fence analogy. The second and third images illustrates how a polarizer selects a certain component of the electric field, reducing the field by a factor equal to cosθ, where θ is the angle between two consecutive polarizing filters. Since wave energy is proportional to the square of the electric field, the fraction of the number of photons that pass the second filter is cos2θ. Hence the probability that any given photon will pass the second filter is also equal to cos2θ.
"De facto" polarization measurements
[edit | edit source]
The "trick" behind a Bell's theorem experiment lies in an observed correlation in polarization between Alice and Bob. Depending on the atomic transition employed to create the entangled pair, the polarizations are either aligned or perpendicular to each other whenever the two filters are aligned in this fashion. This correlation can be demonstrated by attaching a wooden block to a stretched snaky spring. The block acts as the parent atom which emits two pulses when struck by a pulse generated at one end.
There is an important distinction between this demonstration with a classical wave and a Bell's theorem experiment: The polarization of the outgoing waves was "known" before they were emitted.
Illustrating the the odds of winning solitaire version of the card game
[edit | edit source]
A card game for Bell's theorem and its loopholes models a situation where the polarizers' orientation differs by 60°. By the familiar right triangle, we see that , so that the particles will win with a 75% probability. In this symmetric case, the sum of three probabilities for getting the same answers , while Bell's inequality stipulates that it be greater than unity.
Non-interacting particles in a narrow tube
[edit | edit source]
Now consider two non-interacting particles travelling in opposite directions, confined to lie inside a tube of infinite length and radius R. To avoid complicated symmetries among identical particles, we assume the particles are distinguishable. They could be assigned different masses, but we shall not do that here to keep the algebra as simple as possible. The particles do not possess intrinsic spin.
The "parent atom" exists only for a brief instant at time, t=0, as the wavepackets overlap to form a standing wave.[1] We shall exploit certain well-known symmetries during this brief time of overlapping wavepackets in order to place constraints on the wavepackets after they have been separated and subject to remote measurements. To emulate polarization, we assume that an infinite cylindrical potential well demands that the wavefunction vanish at r = R, and select modes associated with a 2p state. In polar coordinates, the two-dimensional wavefunction is, ψ ∝ J1(k11r)cosθ, where J1 is a Bessel function, and the radial wavenumber is selected so that k11R is the first zero of that Bessel function.[2]
This wavefunction also describes the vibrations of a circular membrane, with two exceptions:
- The time-independent eigenfunctions of quantum particles match those of a vibrating membrane only in the limit that the wavelength along the tube is infinitely long.
- The frequency spectrum of vibrating membranes does not match the quantum energy levels because stretched membrane modes and the w:Schrödinger equation have different dispersion relations.
It takes two to entangle
[edit | edit source]The reader is asked to inspect the three normal modes (1s, 2p, 2s) on a vibrating circular membrane (above and to the right). The 1s and 2s modes are azimuthally symmetrical, meaning that as you walk around the mode, it seems to look the same. The 2p mode is not. It is one of two degenerate modes, the other 2p state having a node line perpendicular to the one shown in the figure.[3] Can a mixture of these two degenerate p modes create azimuthal symmetry? Absolutely not. The superposition of the two 2p degenerate modes will either produce a 2p state with a node line in a different direction, or perhaps a circular or elliptical wave. To create a circular wave, move a cup of coffee in a circular fashion. The sloshing coffee will be circularly polarized. But...in the next section we will show that two cups with different waves spinning in the opposite direction can achieve this azimuthal symmetry. If the parent atom jumps between two azimuthal quantum states as it emits a pair of photons, that pair must possess azimuthal symmetry. In other words: It takes two to entangle.
Dirac notation
[edit | edit source]The Hamiltonian for two non-interacting particles confined to lie within a circle of radius R is:
where the unprimed variables refer to Alice and the primed variables refer to Bob. While this Hamiltonian allows us to recover a simple model for entanglement, it is incomplete in two respects:
- We neglect variation in the z direction because the particle is assumed to have virtually zero kinetic energy in that direction. By the Heisenberg uncertainty principle, this implies that the particle is not very localized in that direction. At time we assume that variation in z is either or , where , which allows us to neglect that part of the Hamiltonian for kinetic energy. It is important that either the cosine or the sine function describes the state. A mixture of the sine and cosine state fails to create the necessary correlation (anticorrelation) when the polarization angles are the same.
- There is an infinite potential that sets the wave amplitude to zero at the edge of the tube. This boundary conditions suggests a change of variables from to polar coordinates for each particle . The 2p mode of a streched membrane has two independent normal modes (involving sinθ and cosθ), which yields four independent modes for the two particles.
While Dirac's bra–ket notation is generally associated with Matrix mechanics, it can also be used to remove the clutter when attempting to define wavefunctions. Define:
These two functions of (x,y) or equivalently of (r,θ) describe the amplitude of the 1p state of a stretched membrane. The factor is a normalization constant that we shall not require in this argument. We shall construct our entangles state by superimposing the following four wavefunctions, which are products of wavefunctions of the form, . In Dirac notation, these four wavefunctions can be further simplified and written as:
Rotational invariance
[edit | edit source]The first step towards quantum entanglement is an interesting observation regarding two linear combinations of these states:
This transition from four independent modes to only two is significant because each of the two states shown above depend on the difference between the angles . Consequently if we rotate our coordinate system by any arbitrary angle, then both angles will change by the same amount, but the difference between and remains the same. Therefore the combined wave amplitude remains unchanged. Hence, even though these modes depend on each angle, the wavefunction does not change if the system is rotated. This property is known as rotational invariance, and can be imposed on emitted photons (or daughter nuclides in nuclear transitions) provided the the states of the parent atom before and after emission are also invariant to rotations..
Imposing rotational invariance on our entangled state reduces the number of allowed states from four to only two. But to achieve quantum entanglement, it is necessary to reduce this to only one allowed state for the two particles in a tube.
Introduction to parity
[edit | edit source]In three dimensions, the parity operator reverses either one or three of the axes that define the three linear dimensions. Parity is often preserved in atomic an nuclear transitions, so that knowledge of the parent atom's parity before and after the transition will stipulate which parity is associated with the entangled pair of radiated particles. Here, we shall restrict our discussion to parity in just the two transverse dimensions.
It is important to establish either even or odd parity for the entangled pair, because only this yields the required correlation (or anti-correlation) between the measurement of Alice and Bob. For example, to ensure correlation, we would require the even (two-dimensional) parity:
The rules of quantum mechanics stipulate that a measurement changes the system. If Alice is found to be in the x-polarization, then the entire system "collapses" to the state and Bob is x-polaarized. Likewise, if Alice is y-polarized, Bob will also be y-polarized polarized.
It is important to know that this correlation is not restricted to polarization measurements along the x and y axes. Suppose the system is viewed in a rotated coordinate frame. The results of wikipedia:Rotation matrix may be used. To avoid confusion, we relabel the rotation angle and avoid the use of primes (used here to distinguish between the wavefunctions associated with Alice and Bob). The following describes a rotation by the angle to both the coordinates for Alice, well as Bob's variables :
For the even-parity case discussed here, if Alice is polarized along the axis, Bob will be observed to be polarized along the same axis.
A polarizing filter for this system
[edit | edit source]
The student may wonder why instead of subjecting the photons to polarizing filters to see if the photon was oriented parallel or perpendicular to a given axis, the polarization orientation isn't instead measured directly. The answer is beyond the scope of this discussion and involves the Heisenberg's uncertainty principle, which places restrictions on what can and cannot be measured. But, we can show how a polarizing filter can be constructed for our particles in a narrow tube: At some point after the two entangled particles have separated, cut a very narrow slit along the axis. The wave inside will leak out in a fashion familiar to those who study acoustics. Each wavefunction can be viewed as a superposition of two waves with nodes parallel and perpendicular to that slit. If the particle is detected inside the tube it had one linear polarization, if not, it had the other (perpendicular) polarization. Like most physical measurements, the results will be slightly inconclusive: If the slit is too wide, the entire wavefunction escapes too quickly. If it is too narrow, it takes an infinite amount of time (i.e. length) for half of the wave to leak out.
- Challenge question: What are the required slit dimensions (width and length) required to overcome the detector failure loophole?
Footnotes
[edit | edit source]- ↑ One could repair this blemish by creating a barrier potential to contain the particles as they tunnel out, but that complication is unnecessary in this introductory peek at entanglement.
- ↑ For approximations for this Bessel function, see http://www.dam.brown.edu/people/mariom/AM282-01/HANDOUTS/Abramowitz_Stegun_Chapter_9.pdf Approximation for J_1 Bessel fctn
- ↑ Wikipedia:Node_(physics) currently defines a node as a point on a vibrating string or thin rod. When the object is a two dimensional plane, this region of zero motion becomes a one-dimensional curve. in three dimensions it the node becomes a two-dimensional surface.