Why is the Sky dark at Night?

This essay is intended to accompany a well-known You-tube video

Watch: Why is it Dark at Night?

Olber's Paradox

Olbers' paradox in action

• Most of this material was taken from Wikipedia.

The VIDEO you just watched starts with Olber's Paradox

In astrophysics and physical cosmology, Olbers' paradox, named after the German astronomer Heinrich Wilhelm Olbers (1758–1840) and also called the "dark night sky paradox", is the argument that the darkness of the night sky conflicts with the assumption of an infinite and eternal static universe. The darkness of the night sky is one of the pieces of evidence for a non-static universe such as the Big Bang model. If the universe is static and populated by an infinite number of stars, any sight line from Earth must end at the (very bright) surface of a star, so the night sky should be completely bright. This contradicts the observed darkness of the night.

Edward Robert Harrison's Darkness at Night: A Riddle of the Universe (1987) gives an historical account of the dark night sky paradox. Harrison claims that the first to conceive of anything like the paradox was Thomas Digges, who postulated an infinite universe with infinitely many stars. Kepler also posed the problem in 1610, and the paradox took its mature form in the 18th century work of Halley and Cheseaux. The paradox is commonly attributed to the German amateur astronomer Heinrich Wilhelm Olbers, who described it in 1823, but Harrison shows convincingly that Olbers was far from the first to pose the problem, nor was his thinking about it particularly valuable. Harrison argues that the first to set out a satisfactory resolution of the paradox was Lord Kelvin, in a little known 1901 paper, and that Edgar Allan Poe's essay Eureka (1848) curiously anticipated some qualitative aspects of Kelvin's argument:

“ Were the succession of stars endless, then the background of the sky would present us a uniform luminosity, like that displayed by the Galaxy – since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all. ”

Every line of sight ends on a star.

The paradox is that a static, infinitely old universe with an infinite number of stars distributed in an infinitely large space would be bright rather than dark.

To show this, we divide the universe into a series of concentric shells, 1 light year thick (say). Thus, a certain number of stars will be in the shell 1,000,000,000 to 1,000,000,001 light years away, say. If the universe is homogeneous at a large scale, then there would be four times as many stars in a second shell between 2,000,000,000 to 2,000,000,001 light years away. However, the second shell is twice as far away, so each star in it would appear four times dimmer than the first shell. Thus the total light received from the second shell is the same as the total light received from the first shell.

Thus each shell of a given thickness will produce the same net amount of light regardless of how far away it is. That is, the light of each shell adds to the total amount. Thus the more shells, the more light. And with infinitely many shells there would be a bright night sky.

Dark clouds could obstruct the light. But in that case the clouds would heat up, until they were as hot as stars, and then radiate the same amount of light.

Kepler saw this as an argument for a finite observable universe, or at least for a finite number of stars. We can only imagine what Poe saw in all this.

How Do We Know the Age of the Universe?

Fit of redshift velocities to Hubble's law. Shown are redshifts versus distance for type Ia superovae. H₀ is slope of the straight line.

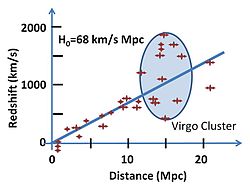
If one looks at very distant galaxies, the redshift of spectral lines indicate that these galaxies are all receding. The velocity of each galaxy (towards or away from us) can be measured using the redshift of the spectral lines. The distance can be estimated by observing supernovae. The conclusion is that the average speed (away) is directly proportional to the distance. The slope of this line gives us an estimate of the age of the universe. From the graph shown to the right, the slope is approximately

${\begin{aligned}{\frac {1}{H_{0}}}&={\frac {\text{Mpc}}{68{\text{ km/s}}}}={\frac {\text{distance}}{\text{distance/time}}}={\text{time}}\\&={\frac {10^{6}}{68\times 10^{3}}}{\frac {{\text{pc}}\cdot {\text{s}}}{\text{m}}}\left({\frac {3.086\times 10^{16}{\text{ m}}}{1{\text{pc}}}}\right)\left({\frac {\text{year}}{3.171\times 10^{7}{\text{ s}}}}\right)\\&\approx 14.3{\text{ billion years}}\end{aligned}}$

How Do We Know the Distances to the Galaxies?

SN 1994D in NGC 4526 galaxy

To calculate the distance to a source of light you need to know how bright an object seems to be from your distance, as well as how bright the object really is. The technical term for these two different definitions of brightness are apparent magnitude(how bright it seems to be). absolute magnitude (how bright it really is). and Any astronomical object of known absolute magnitude is called a standard candle. An important standard candle is the supernovae, which is so bright it can outshine an entire galaxy.

These supernovae have names (See Names of supernovae) and type classifications. For example, the bright spot in the outskirts of of the NGC 4526 galaxy is known as SN 1994D, which is a Type Ia supernova type. It was discovered by a relatively small (30-inch) telescope at Leuschner Observatory.

Cosmic distance ladder

It was not easy to determine the absolute magnitude of supernovae because there are several types. Fortunately, while they are rare in any given galaxy, there are so many galaxies that they are commonly observed, often using automated telescopes. (The estimated rate of supernova production in a galaxy the size of the Milky Way is about one every 50 years.) The fourth of 41 supernovae observed in 1994 was SN1994D, and the rate of documented supernovae in the sky has increased significantly since then. .

To determine the absolute magnitude of a typical supernovae, astronomers had to wait for supernovae in galaxies that were sufficiently close to us that the distance to the galaxy was already known. The astronomers could then use the known distance and the apparent magnitude to calculate the absolute magnitude.

But how could they determine the distance to nearby galaxies? Those galaxies were close enough so that other (less luminous) standard candles could be used. In other words they could use dimmer but more abundant standard candles, such as certain types of stars that could be identified through their spectral lines, or due to the fact that they are variable stars. It takes many rungs of the cosmic distance ladder to put the pieces together.

How Do We Know the Speeds of the Galaxies?

Redshift of spectral lines ifor a supercluster of distant galaxies (right), as compared to that of the Sun (right)

If a galaxy is moving towards or away from us, this component of the velocity can be measured using the Doppler shift. The Doppler Effect can is most easily explained using the "wave" picture of light, as a shift in the wavelength that occurs when the source of a wave is moving. A stationary sound source produces sound waves at a constant frequency with wave-fronts propagate symmetrically away from the source in all directions. But if the sound source is moving the wavelengths are shorter in front of the moving object, and longer behind it.

moving source

Even swans make a Doppler shift.

Quiz

See the subpage for a quiz on this topic.