University of Florida/Eml4507/s13 Team 3 Report 1

Report 1

Problem 1: Completing a Matlab Primer[edit | edit source]

Problem 2: Equation of Motion of a Spring-Mass-Dashpot System[edit | edit source]

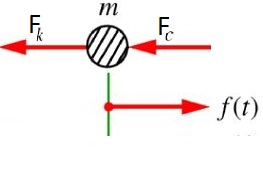
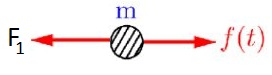
Problem Statement[edit | edit source]

Derive the equation of motions for the two spring-mass-dashpot systems in series.

Solution[edit | edit source]

In order to derive an equation of motion, all of the forces must be analyzed. In the spring-mass-dashpot model there are forces from the spring, driving force, and a damping force.

The force of a spring oriented in the y-direction is given by Hooke's Law:

\displaystyle F_{k}=ky

The force of a damper oriented in the y-direction is:

\displaystyle F_{c}=cy'

Summing the forces with respect to their directions in the Free Body Diagram:

\displaystyle -F_{k}-F_{c}-my''+F(t)=0

Plugging in spring and damper values:

\displaystyle -ky-cy'-my''+F(t)=0

Reorganizing the equation we get: $\displaystyle$

\displaystyle my''+cy'+ky=F(t)

Solution[edit | edit source]

In order to derive an equation of motion, all of the forces must be analyzed. Once again, in the spring-mass-dashpot model there are forces from the spring, driving force, and damping force.

The forces directions with respect to the Free Body Diagram:

\displaystyle my''+F_{1}=F(t)

To find the force from the spring and damper, we set them equal to eachother:

\displaystyle F_{k}=F_{c}

\displaystyle ky_{k}=Cy'_{c}

Solving for dampers velocity: Summing the forces with respect to their directions in the Free Body Diagram:

\displaystyle y''_{c}=y_{k}{\frac {k}{c}}

Plugging into acceleration equations after taking the derivative:

\displaystyle y''=y''_{c}+y''_{k}

\displaystyle y''=y''_{k}+y'_{k}{\frac {k}{c}}

Plugging into the original: $\displaystyle$

\displaystyle m(y''_{k}+y_{k}{\frac {k}{c}})+ky_{k}=F(t)

Problem 3: Finding the numerical values for the element stiff matrices k⁽¹⁾ and k⁽²⁾[edit | edit source]

Problem Statement[edit | edit source]

Part 1: Provide the numerical values for the element stiffness matrices $\mathbf {k^{(1)}}$ and $\mathbf {k^{(2)}}$ .

Part 2: Find the coordinates of the global nodes 1 and 3 when the global node 2 is at the origin of the global coordinate system.

The following are physical parameters:

$E^{(1)}=3,E^{(2)}=5,$

$A^{(1)}=1,A^{(2)}=2,$

$L^{(1)}=4,L^{(2)}=2$

$\theta ^{(1)}=30^{o},\theta ^{(2)}=-45^{o}$

Problem Solution[edit | edit source]

$\mathbf {k^{(e)}} =k^{(e)}{\begin{bmatrix}(l^{(e)})^{2}&l^{(e)}m^{(e)}&-(l^{(e)})^{2}&-l^{(e)}m^{(e)}\\l^{(e)}m^{(e)}&(m^{(e)})^{2}&-l^{(e)}m^{(e)}&-(m^{(e)})^{2}\\-(l^{(e)})^{2}&-l^{(e)}m^{(e)}&(l^{(e)})^{2}&l^{(e)}m^{(e)}\\-l^{(e)}m^{(e)}&-(m^{(e)})^{2}&l^{(e)}m^{(e)}&(m^{(e)})^{2}\end{bmatrix}}$

where

$l^{(e)}=cos(\theta ^{(e)}),m^{(e)}=sin(\theta ^{(e)})$

and

$k^{(e)}={\frac {E^{(e)}A^{(e)}}{L^{(e)}}}$

As given in the problem statement,

$E^{(1)}=3,E^{(2)}=5,$

$A^{(1)}=1,A^{(2)}=2,$

$L^{(1)}=4,L^{(2)}=2$

$\theta ^{(1)}=30^{o},\theta ^{(2)}=-45^{o}$

Therefore,

$k^{(1)}={\frac {3*1}{4}}={\frac {3}{4}},k^{(2)}={\frac {5*2}{2}}=5,$

$(l^{(1)})^{2}=.75,(m^{(1)})^{2}=.25,l^{(1)}m^{(1)}=.433$

and

$(l^{(2)})^{2}=.5,(m^{(2)})^{2}=.5,l^{(2)}m^{(2)}=-.5$

Substituting these values back into the original stiffness matrix, $\mathbf {k^{(e)}}$ yields:

$\mathbf {k^{(1)}} =.75{\begin{bmatrix}.75&.433&-.75&-.433\\.433&.25&-.433&-.25\\-.75&-.433&.75&.433\\-.433&-.25&.433&.25\end{bmatrix}}={\begin{bmatrix}.5625&.3248&-.5625&-.3248\\.3248&.1875&-.3248&-.1875\\-.5625&-.3248&.5625&.3248\\-.3248&-.1875&.3248&.1875\end{bmatrix}}$

and

$\mathbf {k^{(2)}} =5{\begin{bmatrix}.5&-.5&-.5&.5\\-.5&.5&.5&-.5\\-.5&.5&.5&-.5\\.5&-.5&-.5&.5\end{bmatrix}}={\begin{bmatrix}2.5&-2.5&-2.5&2.5\\-2.5&2.5&2.5&-2.5\\-2.5&2.5&2.5&-2.5\\2.5&-2.5&-2.5&2.5\end{bmatrix}}$

Part 2[edit | edit source]

Global Nodes 1 and 2 can be located in our coordinate system using the angle and length of each respective element.

However, each angle must be measured from the right horizontal on global node 2. $\theta ^{(2)}$ remains the same, but $\theta ^{(1)}=210^{o}$ .

Trigonometry shows that the coordinates of global nodes 1 and 3,

$(x_{1},y_{1})$ and $(x_{2},y_{2})$

can be written as

$(L^{(1)}cos(\theta ^{(1)}),L^{(1)}sin(\theta ^{(1)}))$ and $(L^{(2)}cos(\theta ^{(2)}),L^{(2)}sin(\theta ^{(2)}))$ respectively.

Therefore, global nodes 1 and 3 have the following coordinates:

$(-2{\sqrt {3}},-2)$ and $(2{\sqrt {2}},-2{\sqrt {2}})$

Problem 4: Analysis of a truss with three members in CALFEM[edit | edit source]

  On my honor, I have neither given nor received unauthorized aid in doing this assignment.

Problem Statement[edit | edit source]

Consider a plane truss consisting of tree bars with the properties E = 200 GPa, A₁ = 6.0 · 10^-4 m², A₂ = 3.0 · 10^-4 m² and A₃ = 10.0 · 10^-4 m², and loaded by a single force P = 80 kN. The corresponding finite element model consists of three elements and eight degrees of freedom. ^[3]

Solution[edit | edit source]

The free body diagram is defined by the matrix

  Edof=[1 1 2 5 6; 
        2 5 6 7 8; 
        3 3 4 5 6];

Where the first number in each row is the element, and the four other numbers are the degrees of freedom at each node of the element.

Next, create the n x n stiffness matrix K, and the n x 1 load vector f

  >> K=zeros(8);
     f=zeros(8,1); f(6)=-80e3;

The axial rigidity of the elements are defined by the element property vectors

  >> E=2.0e11;
  >> A1=6.0e-4;    A2=3.0e-4;   A3=10.0e-4;
  >> ep1=[E A1];   ep2=[E A2];   ep3=[E A3];

and the element coordinate vectors ex1, ex2, ex3, ey1, ey2, ey3

  >> ex1=[0 1.6];   ex2=[1.6 1.6];   ex3=[0 1.6];
  >> ey1=[0 0];   ey2[0 1.2];   ey3=[1.2 0];

Using bar2e, compute Ke1, Ke2, and Ke3

  >> Ke1=bar2e(ex1,ey1,ep1)
  Ke1 = 
  1.0e+007 * 
  7.5000    0   -7.5000    0
       0    0         0    0
 -7.5000    0    7.5000    0
       0    0         0    0
  
  >> Ke2=bar2e(ex2,ey2,ep2)
  Ke2 = 
  1.0e+007 * 
  0         0    0         0
  0    5.0000    0   -5.0000
  0   -5.0000    0    5.0000
  
  >> Ke3=bar2e(ex3,ex3,ep3)
  Ke3 = 
  1.0e+007 *
  6.4000   -4.8000   -6.4000   4.8000
 -4.8000    3.6000    4.8000  -3.6000
 -6.4000    4.8000    6.4000  -4.8000
  4.8000   -3.6000   -4.8000   3.6000

Assemble the element stiffness matrices to create the global stiffness matrix

  >> K=assem(Edof(1,:),K,Ke1);
  >> K=assem(Edof(2,:),K,Ke2);
  >> K=assem(Edof(3,:),K,Ke3)
  
  K = 
  1.0e+008 *
  0.7500    0        0        0   -0.7500         0    0         0
       0    0        0        0         0         0    0         0
       0    0   0.6400   -4.800   -0.6400    0.4800    0         0
       0    0        0        0         0         0    0         0
       0    0  -0.6400    4.800    1.3900   -0.4800    0         0
       0    0   0.4800   -3.600   -0.4800    0.8600    0   -0.5000
       0    0        0        0         0         0    0         0
       0    0        0        0         0   -0.5000    0    0.5000

Create a prescribed displacement matrix bc

  >> bc=[1 0;2 0;3 0;4 0;7 0;8 0];

Then solve the system of equations using solveq, which results in displacements a and support forces r

  >> [a,r]=solveq(K,f,bc)
  a =
  1.0e-002 *
        0
        0
        0
        0
  -0.0398
  -0.1152
        0
        0
  
  r =
  1.0e+004 *
   2.9845
        0
  -2.9845
   2.2383
   0.0000
   0.0000
        0
   5.7617

From the displacement matrix, it can be seen that the vertical displacement at the point of loading is 1.15 mm. Obtain the element displacements ed1, ed2, and ed3 using extract.

  >> ed1=extract(Edof(1,:),a);
  >> ed2=extract(Edof(2,:),a);
  >> ed3=extract(Edof(3,:),a);

Then calculate the normal forces N1, N2, and N3 using bar2s.

  >> N1=bar2s(ex1,ey1,ep1,ed1)
  N1 =
  -2.9845e+004
  
  >> N2=bar2s(ex2,ey2,ep2,ed2)
  N2 =
  5.7617e+004
     
  >> N3=bar2s(ex3,ey3,ep3,ed3)
  N3 =
  3.7306e+004

The normal forces are N₁ = −29.84 kN, N₂ = 57.62 kN and N₃ = 37.31 kN.

Problem 5: Derivation of standard L2-ODE-CC[edit | edit source]

Problem Statement[edit | edit source]

$\lambda _{1}=-0.5\lambda _{2}=-1.5$
$\lambda _{1}=\lambda _{2}=-0.5$
$\lambda _{1},_{2}=-0.5+i2$

For each case find the standard L2-ODE-CC and the homogeneous solution. Plot each individual solution, and plot all solutions together for comparison

Case 1[edit | edit source]

$(\lambda -\lambda _{1})(\lambda -\lambda _{2})=0$
$(\lambda +.5)(\lambda +1.5)=0$
$\lambda ^{2}+2\lambda +0.75=0$

The standard L2-ODE-CC is then
$y''+2y'+.75=0$

Homogeneous solution
$y_{h}=c_{1}e^{-.5x}+c_{2}e^{-1.5x}$
$y'_{h}=-.5c_{1}e^{-.5x}-1.5c_{2}e^{-1.5x}$
Plug in initial values
$y(0)=1=c_{1}+c_{2}$
$y'(0)=0=-.5c_{1}-1.5c_{2}$

$c_{1}=1-c_{2}$
$0=-.5(1-c_{2})-1.5c_{2}$
$.5=-1c_{2}$
$c_{2}=-.5$
$c_{1}=1.5$

The solution is then
$y_{h}=1.5e^{-.5x}-.5e^{-1.5x}$

Case 2[edit | edit source]

$(\lambda -\lambda _{1})(\lambda -\lambda _{2})$
$(\lambda +.5)(\lambda +.5)$
$\lambda ^{2}+1\lambda +0.25=0$

The standard L2-ODE-CC is then
$y''+y'+.25=0$

Homogeneous solution
$y_{h}=c_{1}e^{-.5x}+c_{2}xe^{-.5x}$
$y'_{h}=-.5c_{1}e^{-.5x}+c_{2}(e^{-.5x}-.5xe^{-.5x}$
Plug in initial values
$y(0)=1=c_{1}$
$y'(0)=0=-.5c_{1}+c_{2}$

$c_{1}=1$
$0=-.5c_{1}+c_{2}$
$0=-.5+c_{2}$
$c_{2}=.5$

The solution is then
$y_{h}=e^{-.5x}-.5xe^{-.5x}$

Case 3[edit | edit source]

$(\lambda -\lambda _{1})(\lambda -\lambda _{2})$
$(\lambda +.5+i2)(\lambda +.5-i2)$
$\lambda ^{2}+.5\lambda -i2\lambda +.5\lambda +.25+.5i2+i2\lambda -.5i2+4$
$\lambda ^{2}+1\lambda +4.25=0$

The standard L2-ODE-CC is then
$y''+y'+4.25y=0$

Homogeneous solution
$y_{h}=e^{-.5x}(c_{1}cos(2x)+c_{2}sin(2x))$
$y'_{h}=-.5e^{-.5x}(c_{1}cos(2x)+c_{2}sin(2x))+e^{-.5x}(-2c_{1}sin(2x)+2c_{2}cos(2x))$
Plug in initial values
$y(0)=1=1*(c_{1}+0)$
$y'(0)=0=-.5(c_{1}+0)+1*(0+2c_{2})$

$c_{1}=1$
$0=-.5c_{1}+2c_{2}$
$.5=2c_{2}$
$c_{2}=.25$

The solution is then
$y_{h}=e^{-.5x}(cos(2x)+.25sin(2x))$

Problem 6: Computing the element stiffness matrices for elements in a truss system[edit | edit source]

Matlab Code[edit | edit source]

Define Input/Output Variables[edit | edit source]

The program begins with the definition of the input and output variables and then clears any existing variables.

function [K] = stiffness( G )

clear

Global Node Information[edit | edit source]

Then the number of global nodes in the problem is input into the variable "G". An array "g" is then created of size "G" to stor the numbers of each node. Then three arrays "x", "y" and "z" are created of size "G" to store the value of each of the corresponding coordinates of each global node. The user is prompted to enter this information using a for loop that loops "G" times.

%Global Node Information
G = input('Give number of Global Nodes: ');

g = [1:G];
x = zeros(1,G);
y = zeros(1,G);
z = zeros(1,G);

for i=1:G
    fprintf('\nFor Global Node %g \n',i) 
    x(i)=input('x coordinate: ');
    y(i)=input('y coordinate: ');
    z(i)=input('z coordinate: ');
end

Element Information[edit | edit source]

Here the user is prompted to enter the number of elements in the system into variable "E." Then the user is asked if the Young's Modulus and Area is the same for each element in the problem. Afterwards five arrays are constructed; "e" stores the element number information, "l1" stores the global node corresponding to local node one for each element, "l2" stores the global node corresponding to local node two for each element, "Modulus" stores the Young's Modulus for each element and "Area" stores the Area for each element.

%Element Information
E = input('\nGive number of Elements: ');
same_modulus = input('Does each element have the same Modulus (1-yes, 0-no): ');
same_area = input('Does each element have the same Area (1-yes, 0-no): ');

e = [1:E];
l1 = zeros(1,E);
l2 = zeros(1,E);
Modulus = zeros(1,E);
Area = zeros(1,E);

Modulus, Area and Local Node Information[edit | edit source]

Here the program enters a if statement if "same_modulus" is equal to one, then the user is prompted to enter the Young's Modulus for all of the elements. Afterward a if statement is used again for the Area of each element. If "same_modulus" and "same_area" are equal to zero the program enters a for loop that prompts the user to enter the Young's Modulus, area and local node information of each element.

%Receive element modulus and area if it is the same for each element
if(same_modulus==1)
    Modulus(:)=input('\nYoungs Modulus: ');
end
if(same_area==1)
    Area(:)=input('\nArea: ');
end

for i=1:E
    fprintf('\nFor Element %g \n',i) 
    l1(i)=input('Global Node Number for Local Node 1: ');
    l2(i)=input('Global Node Number for Local Node 2: ');
    if(same_modulus~=1)
        Modulus(i)=input('Youngs Modulus: ');
    end
    if(same_area~=1)
        Area(i)=input('Area: ');
    end
end

Element Computation[edit | edit source]

For the computation of the element matrix five arrays have to be defined; "L" is the length of each element, "l" is the director cosine of each element, "m" is the director sine of each element, "n" is, "k_elem" is a 3 by 3 stiffness matrix that can represent the entire 6 by 6 stiffness matrix for each element.

%Element Computation
L = zeros(1,E);
l = zeros(1,E);
m = zeros(1,E);
n = zeros(1,E);
k_elem = zeros(3,3,E);

for i=1:E
    L(i)=sqrt((x(l2(i))-x(l1(i)))^2+(y(l2(i))-y(l1(i)))^2+(z(l2(i))-z(l1(i)))^2);
    l(i)=(x(l2(i))-x(l1(i)))/L(i);
    m(i)=(y(l2(i))-y(l1(i)))/L(i);
    n(i)=(z(l2(i))-z(l1(i)))/L(i);
    
    k_elem(:,:,i) = (Modulus(i)*Area(i))/L(i)*[l(i)*l(i), l(i)*m(i), l(i)*n(i);
                                               m(i)*l(i), m(i)*m(i), m(i)*n(i);
                                               n(i)*l(i), n(i)*m(i), n(i)*n(i)];     
end

Stiffness Matrix Construction[edit | edit source]

This section of code initializes the total stiffness matrix "k." Then several for loops are used to place the "k_elem" matrix into the total stiffness matrix. The code in these for loops places each "k_elem" matrix based on the global node and local node associated with it.

%Stiffness Matrix Construction
k = zeros(3*G,3*G);

for i=1:E
    for j=1:3
        for h=1:3
            k(3*(l1(i)-1)+h,3*(l1(i)-1)+j) = k(3*(l1(i)-1)+h,3*(l1(i)-1)+j) + k_elem(h,j,i);
            k(3*(l1(i)-1)+h,3*(l2(i)-1)+j) = k(3*(l1(i)-1)+h,3*(l2(i)-1)+j) - k_elem(h,j,i);
            k(3*(l2(i)-1)+h,3*(l1(i)-1)+j) = k(3*(l2(i)-1)+h,3*(l1(i)-1)+j) - k_elem(h,j,i);
            k(3*(l2(i)-1)+h,3*(l2(i)-1)+j) = k(3*(l2(i)-1)+h,3*(l2(i)-1)+j) + k_elem(h,j,i);
        end
    end
end

1D or 2D[edit | edit source]

Here the code finds rows and columns in the final stiffness matrix that contain all zeros and removes them from the total stiffness matrix.

%remove rows of zeros if problem is 1D or 2D
for i=1:G
    if(x(:)==0)
        k(3*i-(1+i),:)=[];
        k(:,3*i-(1+i))=[];
    end
    if(y(:)==0)
        k(3*i-i,:)=[];
        k(:,3*i-i)=[];
    end
    if(z(:)==0)
        k(3*i-(i-1),:)=[];
        k(:,3*i-(i-1))=[];       
    end
end

Member Forces[edit | edit source]

Eliminate Unknown Forces[edit | edit source]

The the rows 12, 11 and 8 correspond to the unknown forces so they are removed.

k =

1.0e+03 *

    5.2987         0   -1.3404    1.0053   -2.6179         0         0         0         0         0  -1.3404   -1.0053
         0    4.9985    1.0053   -0.7540         0         0         0         0         0   -3.4906  -1.0053   -0.7540
   -1.3404    1.0053    6.5762   -1.0053         0         0   -2.6179         0   -2.6179         0        0         0
    1.0053   -0.7540   -1.0053    4.2445         0   -3.4906         0         0         0         0        0         0
   -2.6179         0         0         0    3.9583   -1.0053   -1.3404    1.0053         0         0        0         0
         0         0         0   -3.4906   -1.0053    4.2445    1.0053   -0.7540         0         0        0         0
         0         0   -2.6179         0   -1.3404    1.0053    3.9583   -1.0053         0         0        0         0
         0         0         0         0    1.0053   -0.7540   -1.0053    0.7540         0         0        0         0
         0         0   -2.6179         0         0         0         0         0    5.2358         0  -2.6179         0
         0   -3.4906         0         0         0         0         0         0         0    3.4906        0         0
   -1.3404   -1.0053         0         0         0         0         0         0   -2.6179         0   3.9583    1.0053
   -1.0053   -0.7540         0         0         0         0         0         0         0         0   1.0053    0.7540 

>> k_temp=k

k_temp =

   1.0e+03 *

    5.2987         0   -1.3404    1.0053   -2.6179         0         0         0         0         0  -1.3404   -1.0053
         0    4.9985    1.0053   -0.7540         0         0         0         0         0   -3.4906  -1.0053   -0.7540
   -1.3404    1.0053    6.5762   -1.0053         0         0   -2.6179         0   -2.6179         0        0         0
    1.0053   -0.7540   -1.0053    4.2445         0   -3.4906         0         0         0         0        0         0
   -2.6179         0         0         0    3.9583   -1.0053   -1.3404    1.0053         0         0        0         0
         0         0         0   -3.4906   -1.0053    4.2445    1.0053   -0.7540         0         0        0         0
         0         0   -2.6179         0   -1.3404    1.0053    3.9583   -1.0053         0         0        0         0
         0         0         0         0    1.0053   -0.7540   -1.0053    0.7540         0         0        0         0
         0         0   -2.6179         0         0         0         0         0    5.2358         0  -2.6179         0
         0   -3.4906         0         0         0         0         0         0         0    3.4906        0         0
   -1.3404   -1.0053         0         0         0         0         0         0   -2.6179         0   3.9583    1.0053
   -1.0053   -0.7540         0         0         0         0         0         0         0         0   1.0053    0.7540 

>> k_temp(12,:)=[]

k_temp =

   1.0e+03 *

    5.2987         0   -1.3404    1.0053   -2.6179         0         0         0         0         0   -1.3404   -1.0053
         0    4.9985    1.0053   -0.7540         0         0         0         0         0   -3.4906   -1.0053   -0.7540
   -1.3404    1.0053    6.5762   -1.0053         0         0   -2.6179         0   -2.6179         0         0         0
    1.0053   -0.7540   -1.0053    4.2445         0   -3.4906         0         0         0         0         0         0
   -2.6179         0         0         0    3.9583   -1.0053   -1.3404    1.0053         0         0         0         0
         0         0         0   -3.4906   -1.0053    4.2445    1.0053   -0.7540         0         0         0         0
         0         0   -2.6179         0   -1.3404    1.0053    3.9583   -1.0053         0         0         0         0
         0         0         0         0    1.0053   -0.7540   -1.0053    0.7540         0         0         0         0
         0         0   -2.6179         0         0         0         0         0    5.2358         0   -2.6179         0
         0   -3.4906         0         0         0         0         0         0         0    3.4906         0         0
   -1.3404   -1.0053         0         0         0         0         0         0   -2.6179         0    3.9583    1.0053

>> k_temp(11,:)=[]

k_temp =

   1.0e+03 *

    5.2987         0   -1.3404    1.0053   -2.6179         0         0         0         0         0   -1.3404   -1.0053
         0    4.9985    1.0053   -0.7540         0         0         0         0         0   -3.4906   -1.0053   -0.7540
   -1.3404    1.0053    6.5762   -1.0053         0         0   -2.6179         0   -2.6179         0         0         0
    1.0053   -0.7540   -1.0053    4.2445         0   -3.4906         0         0         0         0         0         0
   -2.6179         0         0         0    3.9583   -1.0053   -1.3404    1.0053         0         0         0         0
         0         0         0   -3.4906   -1.0053    4.2445    1.0053   -0.7540         0         0         0         0
         0         0   -2.6179         0   -1.3404    1.0053    3.9583   -1.0053         0         0         0         0
         0         0         0         0    1.0053   -0.7540   -1.0053    0.7540         0         0         0         0
         0         0   -2.6179         0         0         0         0         0    5.2358         0   -2.6179         0
         0   -3.4906         0         0         0         0         0         0         0    3.4906         0         0


>> k_temp(8,:)=[]

k_temp =

   1.0e+03 *

    5.2987         0   -1.3404    1.0053   -2.6179         0         0         0         0         0   -1.3404   -1.0053
         0    4.9985    1.0053   -0.7540         0         0         0         0         0   -3.4906   -1.0053   -0.7540
   -1.3404    1.0053    6.5762   -1.0053         0         0   -2.6179         0   -2.6179         0         0         0
    1.0053   -0.7540   -1.0053    4.2445         0   -3.4906         0         0         0         0         0         0
   -2.6179         0         0         0    3.9583   -1.0053   -1.3404    1.0053         0         0         0         0
         0         0         0   -3.4906   -1.0053    4.2445    1.0053   -0.7540         0         0         0         0
         0         0   -2.6179         0   -1.3404    1.0053    3.9583   -1.0053         0         0         0         0
         0         0   -2.6179         0         0         0         0         0    5.2358         0   -2.6179         0
         0   -3.4906         0         0         0         0         0         0         0    3.4906         0         0

Eliminate Known Displacements[edit | edit source]

The columns 12, 11 and 8 correspond to the known displacements so they are removed.

>> k_temp(:,12)=[]

k_temp =

  1.0e+03 *

    5.2987         0   -1.3404    1.0053   -2.6179         0         0         0         0         0   -1.3404
         0    4.9985    1.0053   -0.7540         0         0         0         0         0   -3.4906   -1.0053
   -1.3404    1.0053    6.5762   -1.0053         0         0   -2.6179         0   -2.6179         0         0
    1.0053   -0.7540   -1.0053    4.2445         0   -3.4906         0         0         0         0         0
   -2.6179         0         0         0    3.9583   -1.0053   -1.3404    1.0053         0         0         0
         0         0         0   -3.4906   -1.0053    4.2445    1.0053   -0.7540         0         0         0
         0         0   -2.6179         0   -1.3404    1.0053    3.9583   -1.0053         0         0         0
         0         0   -2.6179         0         0         0         0         0    5.2358         0   -2.6179
         0   -3.4906         0         0         0         0         0         0         0    3.4906         0

  
>> k_temp(:,11)=[]

k_temp =

   1.0e+03 *

    5.2987         0   -1.3404    1.0053   -2.6179         0         0         0         0         0
         0    4.9985    1.0053   -0.7540         0         0         0         0         0   -3.4906
   -1.3404    1.0053    6.5762   -1.0053         0         0   -2.6179         0   -2.6179         0
    1.0053   -0.7540   -1.0053    4.2445         0   -3.4906         0         0         0         0
   -2.6179         0         0         0    3.9583   -1.0053   -1.3404    1.0053         0         0
         0         0         0   -3.4906   -1.0053    4.2445    1.0053   -0.7540         0         0
         0         0   -2.6179         0   -1.3404    1.0053    3.9583   -1.0053         0         0
         0         0   -2.6179         0         0         0         0         0    5.2358         0
         0   -3.4906         0         0         0         0         0         0         0    3.4906

>> k_temp(:,8)=[]

k_temp =

   1.0e+03 *

    5.2987         0   -1.3404    1.0053   -2.6179         0         0         0         0
         0    4.9985    1.0053   -0.7540         0         0         0         0   -3.4906
   -1.3404    1.0053    6.5762   -1.0053         0         0   -2.6179   -2.6179         0
    1.0053   -0.7540   -1.0053    4.2445         0   -3.4906         0         0         0
   -2.6179         0         0         0    3.9583   -1.0053   -1.3404         0         0
         0         0         0   -3.4906   -1.0053    4.2445    1.0053         0         0
         0         0   -2.6179         0   -1.3404    1.0053    3.9583         0         0
         0         0   -2.6179         0         0         0         0    5.2358         0
         0   -3.4906         0         0         0         0         0         0    3.4906

Calculation of q[edit | edit source]

The matrix "q" is the displacements found using the reduced "k" matrix and the reduced "f" matrix.

>> f_temp=transpose([0 0 0 -1200 400 0 0 0 0])

f_temp =

           0
           0
           0
       -1200
         400
           0
           0
           0
           0

>> q_temp=inv(k_temp)*f_temp

q_temp =

    0.8260
   -1.4993
    0.6112
   -2.1837
    0.5205
   -1.9258
    1.0696
    0.3056
   -1.4993

>> q=transpose([transpose(q_temp(1:7)) 0 transpose(q_temp(8:9)) 0 0])

q =

    0.8260
   -1.4993
    0.6112
   -2.1837
    0.5205
   -1.9258
    1.0696
         0
    0.3056
   -1.4993
         0
         0

Calculation of the Nodal Forces[edit | edit source]

Calculation of the Member Forces[edit | edit source]

>> q_bar=zeros(4,9);
for i=1:E
    T= [l(i) m(i) 0    0
       -m(i) l(i) 0    0
        0    0    l(i) m(i)
        0    0   -m(i) l(i)];
    
    q_bar(:,i)=T*transpose([q(2*l1(i)-1) q(2*l1(i)) q(2*l2(i)) q(2*l2(i)-1)]);
end
>> q_bar

q_bar =

   -1.7991    1.5719   -1.0696    1.4993    0.3056   -0.3056    0.8260         0    1.9258
    1.3802   -1.2284         0    0.8260   -1.4993    1.4993   -1.4993         0    0.5205
    1.6951   -0.6417    2.1837   -0.3056   -2.1837         0   -1.9258   -0.7038   -0.6112
    0.2387    0.8556   -0.6112   -1.4993    0.6112         0    0.5205    1.5604   -2.1837

>> for i=1:E
    k_bar= (Modulus(i)*Area(i))/L(i)*[1  0 -1  0
                                      0  0  0  0
                                     -1  0  1  0
                                      0  0  0  0];
    
    f_bar(:,i)=k_bar*q_bar(:,i);
end
>> f_bar

f_bar =

   1.0e+03 *

   -7.3180    4.6360   -8.5167    6.3000    6.5167   -0.8000    7.2042    1.4740    8.8556
         0         0         0         0         0         0         0         0         0
    7.3180   -4.6360    8.5167   -6.3000   -6.5167    0.8000   -7.2042   -1.4740   -8.8556
         0         0         0         0         0         0         0         0         0

Member Forces[edit | edit source]

Forces in Element 1: Fx1 = -7318, Fy1 = 0, Fx2 = 4636, Fy2 = 0

Forces in Element 2: Fx3 = -8516, Fy3 = 0, Fx4 = 6300, Fy4 = 0

Forces in Element 3: Fx5 = 6516, Fy5 = 0, Fx6 = -800, Fy6 = 0

Forces in Element 4: Fx7 = 7204, Fy7 = 0, Fx8 = 1474, Fy8 = 0

Forces in Element 5: Fx9 = 8855, Fy9 = 0, Fx10 = 7318, Fy10 = 0

Forces in Element 6: Fx11 = -4636, Fy11 = 0, Fx12 = 8516, Fy12 = 0

Forces in Element 7: Fx13 = -6300, Fy13 = 0, Fx14 = -6516, Fy14 = 0

Forces in Element 8: Fx15 = 800, Fy15 = 0, Fx16 = -7204, Fy16 = 0

Forces in Element 9: Fx17 = -1474, Fy17 = 0, Fx18 = -8855, Fy18 = 0

Full Matlab Code[edit | edit source]

 function [k] = stiffness( G )
 
 clear
 
 %Global Node Information
 G = input('Give number of Global Nodes: ');
 
 g = [1:G];
 x = zeros(1,G);
 y = zeros(1,G);
 z = zeros(1,G);
 
 for i=1:G
     fprintf('\nFor Global Node %g \n',i) 
     x(i)=input('x coordinate: ');
     y(i)=input('y coordinate: ');
     z(i)=input('z coordinate: ');
 end
 
 %Element Information
 E = input('\nGive number of Elements: ');
 same_modulus = input('Does each element have the same Modulus (1-yes, 0-no): ');
 same_area = input('Does each element have the same Area (1-yes, 0-no): ');
 
 e = [1:E];
 l1 = zeros(1,E);
 l2 = zeros(1,E);
 Modulus = zeros(1,E);
 Area = zeros(1,E);
 
 %Receive element modulus and area if it is the same for each element
 if(same_modulus==1)
     Modulus(:)=input('\nYoung''s Modulus: ');
 end
 if(same_area==1)
     Area(:)=input('\nArea: ');
 end
 
 for i=1:E
     fprintf('\nFor Element %g \n',i) 
     l1(i)=input('Global Node Number for Local Node 1: ');
     l2(i)=input('Global Node Number for Local Node 2: ');
     if(same_modulus~=1)
         Modulus(i)=input('Young''s Modulus: ');
     end
     if(same_area~=1)
         Area(i)=input('Area: ');
     end
 end
 
 
 %Element Computation
 L = zeros(1,E);
 l = zeros(1,E);
 m = zeros(1,E);
 n = zeros(1,E);
 k_elem = zeros(3,3,E);
 
 for i=1:E
     L(i)=sqrt((x(l2(i))-x(l1(i)))^2+(y(l2(i))-y(l1(i)))^2+(z(l2(i))-z(l1(i)))^2);
     l(i)=(x(l2(i))-x(l1(i)))/L(i);
     m(i)=(y(l2(i))-y(l1(i)))/L(i);
     n(i)=(z(l2(i))-z(l1(i)))/L(i);
     
     k_elem(:,:,i) = (Modulus(i)*Area(i))/L(i)*[l(i)*l(i), l(i)*m(i), l(i)*n(i);
                                                m(i)*l(i), m(i)*m(i), m(i)*n(i);
                                                n(i)*l(i), n(i)*m(i), n(i)*n(i)];     
 end
 
 
 %Stiffness Matrix Construction
 k = zeros(3*G,3*G);
 
 for i=1:E
     for j=1:3
         for h=1:3
             k(3*(l1(i)-1)+h,3*(l1(i)-1)+j) = k(3*(l1(i)-1)+h,3*(l1(i)-1)+j) + k_elem(h,j,i);
             k(3*(l1(i)-1)+h,3*(l2(i)-1)+j) = k(3*(l1(i)-1)+h,3*(l2(i)-1)+j) - k_elem(h,j,i);
             k(3*(l2(i)-1)+h,3*(l1(i)-1)+j) = k(3*(l2(i)-1)+h,3*(l1(i)-1)+j) - k_elem(h,j,i);
             k(3*(l2(i)-1)+h,3*(l2(i)-1)+j) = k(3*(l2(i)-1)+h,3*(l2(i)-1)+j) + k_elem(h,j,i);
         end
     end
 end
 
 %remove rows of zeros if problem is 1D or 2D
 for i=1:G
     if(x(:)==0)
         k(3*i-(1+i),:)=[];
         k(:,3*i-(1+i))=[];
     end
     if(y(:)==0)
         k(3*i-i,:)=[];
         k(:,3*i-i)=[];
     end
     if(z(:)==0)
         k(3*i-(i-1),:)=[];
         k(:,3*i-(i-1))=[];       
     end
 end

References[edit | edit source]

↑ http://upload.wikimedia.org/wikiversity/en/b/b1/Fead.s13.sec53a.djvu FEAD: sec.53a, p.53-2b, Pb-53.1]
↑ http://upload.wikimedia.org/wikiversity/en/d/d5/Iea.s12.sec1.djvu From IEA S12:p.1-4]
↑ Analysis of a plane truss, CALFEM: A Finite Element Toolbox, Version 3.4, p.9.3-9 (pdf p.234)

[1] ttp://upload.wikimedia.org/wikiversity/en/b/b1/Fead.s13.sec53a.djvu FEAD: sec.53a, p.53-2b, Pb-53.1]

[2] ttp://upload.wikimedia.org/wikiversity/en/d/d5/Iea.s12.sec1.djvu From IEA S12:p.1-4]

[3] Analysis of a plane truss, CALFEM: A Finite Element Toolbox, Version 3.4, p.9.3-9 (pdf p.234)

[1]

[2]

[3]

University of Florida/Eml4507/s13 Team 3 Report 1

Contents

Problem 1: Completing a Matlab Primer[edit | edit source]

Problem 2: Equation of Motion of a Spring-Mass-Dashpot System[edit | edit source]

Problem Statement[edit | edit source]

Solution[edit | edit source]

Solution[edit | edit source]

Problem 3: Finding the numerical values for the element stiff matrices k⁽¹⁾ and k⁽²⁾[edit | edit source]

Problem Statement[edit | edit source]

Problem Solution[edit | edit source]

Part 1[edit | edit source]

Part 2[edit | edit source]

Problem 4: Analysis of a truss with three members in CALFEM[edit | edit source]

Problem Statement[edit | edit source]

Solution[edit | edit source]

Problem 5: Derivation of standard L2-ODE-CC[edit | edit source]

Problem Statement[edit | edit source]

Case 1[edit | edit source]

Case 2[edit | edit source]

Case 3[edit | edit source]

Problem 6: Computing the element stiffness matrices for elements in a truss system[edit | edit source]

Matlab Code[edit | edit source]

Define Input/Output Variables[edit | edit source]

Global Node Information[edit | edit source]

Element Information[edit | edit source]

Modulus, Area and Local Node Information[edit | edit source]

Element Computation[edit | edit source]

Stiffness Matrix Construction[edit | edit source]

1D or 2D[edit | edit source]

Member Forces[edit | edit source]

Eliminate Unknown Forces[edit | edit source]

Eliminate Known Displacements[edit | edit source]

Calculation of q[edit | edit source]

Calculation of the Nodal Forces[edit | edit source]

Calculation of the Member Forces[edit | edit source]

Member Forces[edit | edit source]

Full Matlab Code[edit | edit source]

References[edit | edit source]

Navigation menu

University of Florida/Eml4507/s13 Team 3 Report 1

Problem 1: Completing a Matlab Primer[edit | edit source]

Problem 2: Equation of Motion of a Spring-Mass-Dashpot System[edit | edit source]

Problem Statement[edit | edit source]

Solution[edit | edit source]

Solution[edit | edit source]

Problem 3: Finding the numerical values for the element stiff matrices k(1) and k(2)[edit | edit source]

Problem Statement[edit | edit source]

Problem Solution[edit | edit source]

Part 1[edit | edit source]

Part 2[edit | edit source]

Problem 4: Analysis of a truss with three members in CALFEM[edit | edit source]

Problem Statement[edit | edit source]

Solution[edit | edit source]

Problem 5: Derivation of standard L2-ODE-CC[edit | edit source]

Problem Statement[edit | edit source]

Case 1[edit | edit source]

Case 2[edit | edit source]

Case 3[edit | edit source]

Problem 6: Computing the element stiffness matrices for elements in a truss system[edit | edit source]

Matlab Code[edit | edit source]

Define Input/Output Variables[edit | edit source]

Global Node Information[edit | edit source]

Element Information[edit | edit source]

Modulus, Area and Local Node Information[edit | edit source]

Element Computation[edit | edit source]

Stiffness Matrix Construction[edit | edit source]

1D or 2D[edit | edit source]

Member Forces[edit | edit source]

Eliminate Unknown Forces[edit | edit source]

Eliminate Known Displacements[edit | edit source]

Calculation of q[edit | edit source]

Calculation of the Nodal Forces[edit | edit source]

Calculation of the Member Forces[edit | edit source]

Member Forces[edit | edit source]

Full Matlab Code[edit | edit source]

References[edit | edit source]

Navigation menu

Search

Problem 3: Finding the numerical values for the element stiff matrices k⁽¹⁾ and k⁽²⁾[edit | edit source]