University of Florida/Eml4507/s13.team4ever.Wulterkens.R5.4
Appearance
Problem 5.4 Eigenvalues and Eigenvectors for Mode Shape
On my honor, I have neither given nor recieved unauthorized aid in doing this assignment.
Problem Statement
[edit | edit source]Assume the mass density to be 5,000 . Contruct the diagonal mass matrix and find the eigenpairs. With this, design a matlab and calfem program to determine the deformation shape.
Matlab Solution
[edit | edit source]%Constants
p = 5000;
E = 100000000000;
A = 0.0001;
L = 0.3;
%Degree of Freedom
dof = zeros(25,5);
for i = 1:6
j = 2*i-1;
dof(i,:) = [i,j,j+1,j+2,j+3];
end
for i =7:12
j = i*2+1;
dof(i,:) = [i,j,j+1,j+2,j+3];
end
for i = 13:19
j = (i-12)*2-1;
dof(i,:) = [i,j,j+1,j+14,j+15];
end
for i = 20:25
j = (i-19)*2-1;
dof(i,:) = [i,j,j+1,j+16,j+17];
end
%coordinates
pos = zeros(2,14);
for i=1:7
pos(:,i) = [(i-1)*L;0];
pos(:,i+7) = [(i-1)*L;L];
end
%Connections
conn = zeros(2,25);
for i = 1:6
conn(1,i)= i;
conn(2,i)= i+1;
end
for i = 7:12
conn(1,i) = i+1;
conn(2,i) = i+2;
end
for i = 13:19
conn(1,i) = i-12;
conn(2,i) = i-5;
end
for i = 20:25;
conn(1,i) = i-19;
conn(2,i) = i-11;
end
%seperates into x and y coordinates
x = zeros(14,2);
y = zeros(14,2);
for i = 1:25
x(i,:) = [pos(1,conn(1,i)),pos(1,conn(2,i))];
y(i,:) = [pos(2,conn(1,i)),pos(2,conn(2,i))];
end
%Set up K and M matrix
K = zeros(28);
M = zeros(28);
for i = 1:25
xm = x(i,2)-x(i,1);
ym = y(i,2)-y(i,1);
L = sqrt(xm^2+ym^2);
l = xm/L;
m = ym/L;
k = E*A/L*[l^2 l*m -l^2 -l*m;l*m m^2 -l*m -m^2;-l^2 -l*m l^2 l*m;-l*m -m^2 l*m m^2;];
m = L*A*p;
m = [m/2 0 0 0;0 m/2 0 0;0 0 m/2 0;0 0 0 m/2];
Dof = dof(i,2:5);
K(Dof,Dof) = K(Dof,Dof)+k;
M(Dof,Dof) = M(Dof,Dof)+m;
end
%Makes an alternate K and M matrix to calncel rows and columns for boundary
%conditions.
Kr = K;
Mr = M;
Kr([1 15 16],:) = [];
Kr(:,[1 15 16]) = [];
Mr([1 15 16],:) = [];
Mr(:,[1 15 16]) = [];
%Find Eigenvalue and Eigenvector
[Vec Val] = eig(Kr,Mr);
Vec1 = zeros(25,1);
Vec2 = zeros(25,1);
Vec3 = zeros(25,1);
for i = 1:25
Vec1(i) = Vec(i,1);
Vec2(i) = Vec(i,2);
Vec3(i) = Vec(i,3);
end
%Insert back in the values for initial conditions.
Vec1 = [0;Vec1(1:13);0;0;Vec1(14:25)];
Vec2 = [0;Vec2(1:13);0;0;Vec2(14:25)];
Vec3 = [0;Vec3(1:13);0;0;Vec3(14:25)];
%Add the Eigenvectors to the nodes
X1 = zeros(14,1);
Y1 = zeros(14,1);
X2 = zeros(14,1);
X3 = zeros(14,1);
Y2 = zeros(14,1);
Y3 = zeros(14,1);
X = zeros(14,1);
Y = zeros(14,1);
for i = 1:14
X1(i) = Vec1((i*2)-1,1);
Y1(i) = Vec1((i*2),1);
X(i) = pos(1,i);
Y(i) = pos(2,i);
X2(i) = Vec2((i*2)-1,1);
Y2(i) = Vec2((i*2),1);
X3(i) = Vec3((i*2)-1,1);
Y3(i) = Vec3((i*2),1);
end
%plot origional shape
for i = 1:25
xc = [X(conn(1,i)),X(conn(2,i))];
yc = [Y(conn(1,i)),Y(conn(2,i))];
axis([0 2 -1 1])
plot(xc,yc)
hold on
end
X1 = X+-0.1*X1;
Y1 = Y+-0.1*Y1;
%plot mode 1
for i = 1:25
xc = [X1(conn(1,i)),X1(conn(2,i))];
yc = [Y1(conn(1,i)),Y1(conn(2,i))];
axis([0 2 -1 1])
plot(xc,yc,'r')
hold on
end
X2 = X+X2;
Y2 = Y+Y2;
X3 = X-0.9*X3;
Y3 = Y-0.9*Y3;
%plot mode 2
for i = 1:25
xc = [X2(conn(1,i)),X2(conn(2,i))];
yc = [Y2(conn(1,i)),Y2(conn(2,i))];
axis([0 2 -1 1])
plot(xc,yc,'r')
hold on
end
%plot mode 3
for i = 1:25
xc = [X3(conn(1,i)),X3(conn(2,i))];
yc = [Y3(conn(1,i)),Y3(conn(2,i))];
axis([0 2 -1 1])
plot(xc,yc,'r')
hold on
end
References for Matlab code: Team 3 Report 4 Team 7 Report 4
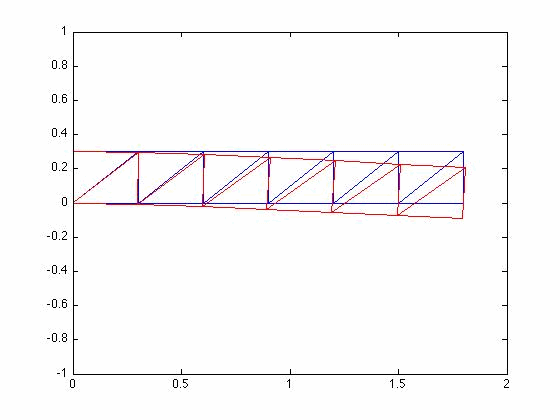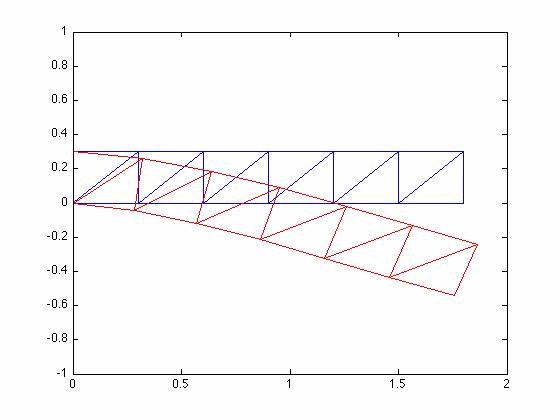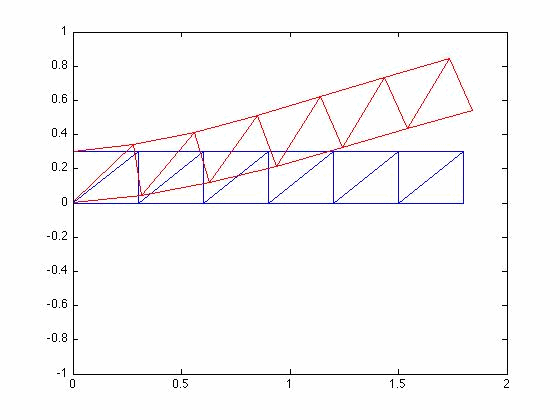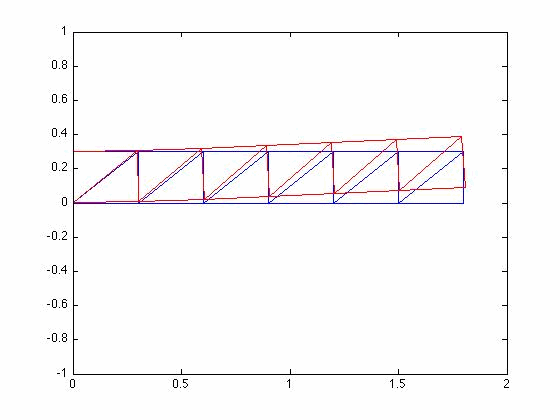
Mode Shapes
[edit | edit source]CALFEM Solution
[edit | edit source]function R4p4
p = 5000; %kg/m3
A = 0.01; %m2
L = 0.3; %m
h = p*A*L;
v = h;
d = (sqrt((L^2)+(L^2)))*A*p;
m = [(h/2)+(d/2)+(v/2);(h/2)+(d/2)+(v/2);
(h/2)+(v/2);(h/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
(h/2)+(v/2);(h/2)+(v/2);
(h/2)+(d/2)+(v/2);(h/2)+(d/2)+(v/2)];
M = diag(m);
Coord = [0 0;0 0.3;0.3 0;0.3 0.3;0.6 0;
0.6 0.3;0.9 0;0.9 0.3;1.2 0;1.2 0.3;
1.5 0;1.5 0.3;1.8 0;1.8 0.3];
Dof = [1 2;3 4;5 6;7 8;9 10;1 12;13 14;15 16;
17 18;19 20;21 22;23 24;25 26;27 28];
Edof = [1 1 2 5 6;2 5 6 9 10;3 9 10 13 14;4 13 14 17 18;5 17 18 21 22;
6 21 22 25 26;7 3 4 7 8;8 7 8 11 12;9 11 12 15 16;10 15 16 19 20;
11 19 20 23 24;12 23 24 27 28;13 1 2 3 4;14 5 6 7 8;15 9 10 11 12;
16 13 14 15 16;17 17 18 19 20;18 21 22 23 24;19 25 26 27 28;20 1 2 7 8;
21 5 6 11 12;22 9 10 15 16;23 13 14 19 20;24 17 18 23 24;25 21 22 27 28];
[Ex,Ey] = coordxtr(Edof,Coord,Dof,2);
K = zeros(28);
ep = [100000000000 0.01];
for i=1:25
Ke = bar2e(Ex(i,:),Ey(i,:),ep);
K = assem(Edof(i,:),K,Ke);
end
[L,X] = eigen(K,M);
eigval = L;
eigvect = X;
Three lowest eigenvalues and eigenvectors
j1eig = eigval(1) j1eigvx = eigvect(:,1) j1eigvy = eigvect(:,2) j2eig = eigval(2) j2eigvx = eigvect(:,3) j2eigvy = eigvect(:,4) j3eig = eigval(3) j3eigvx = eigvect(:,5) j3eigvy = eigvect(:,6) j1eig = -4.1672e-08 j1eigvx = -0.0018 0.0853 0.0136 0.0853 -0.0018 0.0699 0.0136 0.0699 -0.0018 0.0545 0.0136 0.0545 -0.0018 0.0391 0.0136 0.0391 -0.0018 0.0238 0.0136 0.0238 -0.0018 0.0084 0.0136 0.0084 -0.0018 -0.0070 0.0136 -0.0070 j1eigvy = -0.0485 0.0068 -0.0488 0.0068 -0.0485 0.0071 -0.0488 0.0071 -0.0485 0.0074 -0.0488 0.0074 -0.0485 0.0077 -0.0488 0.0077 -0.0485 0.0080 -0.0488 0.0080 -0.0485 0.0083 -0.0488 0.0083 -0.0485 0.0086 -0.0488 0.0086 j2eig = -1.0740e-08 j2eigvx = 0.0155 -0.0334 -0.0053 -0.0334 0.0155 -0.0127 -0.0053 -0.0127 0.0155 0.0081 -0.0053 0.0081 0.0155 0.0289 -0.0053 0.0289 0.0155 0.0496 -0.0053 0.0496 0.0155 0.0704 -0.0053 0.0704 0.0155 0.0912 -0.0053 0.0912 j2eigvy = -0.0242 0.0747 0.0200 0.0761 -0.0197 0.0156 0.0197 0.0202 -0.0092 -0.0374 0.0148 -0.0335 0.0040 -0.0572 0.0040 -0.0572 0.0148 -0.0335 -0.0092 -0.0374 0.0197 0.0202 -0.0197 0.0156 0.0200 0.0761 -0.0242 0.0747 j3eig = 1.2133e-07 j3eigvx = 0.0206 -0.0518 -0.0370 -0.0552 0.0097 0.0333 -0.0347 0.0284 -0.0031 0.0552 -0.0190 0.0633 0.0002 -0.0083 -0.0002 0.0083 0.0190 -0.0633 0.0031 -0.0552 0.0347 -0.0284 -0.0097 -0.0333 0.0370 0.0552 -0.0206 0.0518 j3eigvy = 0.0616 -0.0146 0.0727 -0.0164 0.0453 0.0010 0.0647 -0.0047 0.0125 0.0180 0.0453 0.0165 -0.0204 -0.0017 0.0204 0.0017 -0.0453 -0.0165 -0.0125 -0.0180 -0.0647 0.0047 -0.0453 -0.0010 -0.0727 0.0164 -0.0616 0.0146
Plotting the three lowest mode shapes
for j=1:3
figure
plot(eigvect(:,j));
title(['Mode Shape ',num2str(j)])
end