University of Florida/Eml4507/s13.team4ever.R6

Problem R.6.1

Honor Pledge:

On my honor I have neither given nor received unauthorized aid in doing this problem.

Problem Description:

We are tasked with completing Pb.53.9 on p.53.19b by transforming the generalized eigenvalue problem into a standard eigenvalue problem.

Given

$m_{1}=3,m_{2}=2$
$k_{1}=10,k_{2}=20,k_{3}=15$

Solution

Solving the FBD of both $m_{1}$ and $m_{2}$ gives us the equations of motion.
$m={\begin{bmatrix}m_{1}&0\\0&m_{2}\\\end{bmatrix}}={\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}$
$k={\begin{bmatrix}k_{1}-k_{2}&k_{2}\\k_{2}&-(k_{2}+k_{3})\\\end{bmatrix}}={\begin{bmatrix}-10&20\\20&-35\\\end{bmatrix}}$

Equation of Motion in Matrix Form.

${\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}{\begin{bmatrix}{\ddot {x_{1}}}\\{\ddot {x_{2}}}\\\end{bmatrix}}+{\begin{bmatrix}-10&20\\20&-35\\\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

Now transforming the generalized eigenvalue problem into the standard eigenvalue problem.

$kx={\lambda }mx$ ..............................................(1)

The $m,m^{-1/2},$ and $m^{1/2}$ matrix will be needed so they are solved and provided below.

$m={\begin{bmatrix}3&0\\0&2\\\end{bmatrix}},m^{-1/2}={\begin{bmatrix}1/{\sqrt {3}}&0\\0&1/{\sqrt {2}}\\\end{bmatrix}},m^{1/2}={\begin{bmatrix}{\sqrt {3}}&0\\0&{\sqrt {2}}\\\end{bmatrix}}$

Derivation of the new value $x^{*}$ .First premultiply by $m^{-1/2}$

$m^{-1/2}kx={\lambda }m^{-1/2}mx={\lambda }m^{1/2}x$

Let, $x^{*}=m^{1/2}x$

Then, $x=m^{-1/2}x^{*}$

Plugging Into Eq. 1 above.

$(m^{-1/2}km^{1/2})x^{*}=k^{*}x^{*}={\lambda }x^{*}=0$

Where, $k^{*}=m^{-1/2}km^{1/2}={\begin{bmatrix}3.333&8.165\\8.165&-17.5\\\end{bmatrix}}$

Now, $(k^{*}-{\lambda }I)x^{*}=0$ ............................................(2)

First, Solving for the eigenvalues by setting the determinant of $(k^{*}-{\lambda }I)$ equal to zero.

$det(k^{*}-{\lambda }I)=det({\begin{bmatrix}-3.333-{\lambda }&8.165\\8.165&-17.5-{\lambda }\\\end{bmatrix}})=0$

$(-3.33-{\lambda })(-17.5-{\lambda })=0$

${\lambda }^{2}+20.83{\lambda }-8.392=0$

Solving for ${\lambda }_{1}$ and ${\lambda }_{2}$ using the quadratic.

${\lambda }_{1}=0.395$ and ${\lambda }_{2}=-21.225$

Plugging these values in one at a time into Eq.2 above will yield two respective eigenvectors.

Solving for $x_{1}^{*}$ ,

${\begin{bmatrix}3.333-0.935&8.165\\8.165&-17.50.395\\\end{bmatrix}}{\begin{bmatrix}x_{11}^{*}\\x_{12}^{*}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

$-3.725x_{11}^{*}+8.165x_{12}^{*}=0$
$8.165x_{11}^{*}-17.895x_{12}^{*}=0$

So, $x_{1}^{*}={\begin{bmatrix}2.19\\1\\\end{bmatrix}}$

Now solving for $x_{2}^{*}$ ,

${\begin{bmatrix}3.333+21.225&8.165\\8.165&-17.5+21.225\\\end{bmatrix}}{\begin{bmatrix}x_{21}^{*}\\x_{22}^{*}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

$17.895x_{21}^{*}+8.165x_{22}^{*}=0$
$8.165x_{21}^{*}+3.725x_{22}^{*}=0$

So, $x_{2}^{*}={\begin{bmatrix}-0.456\\1\\\end{bmatrix}}$

Final Solution

Using the transformation $x=M^{-1/2}x^{*}$ , it is possible to obtain the eigenvectors $x_{1}$ and $x_{2}$ .

$x_{1}=M^{-1/2}x_{1}^{*}={\begin{bmatrix}1/{\sqrt {3}}&0\\0&1/{\sqrt {2}}\\\end{bmatrix}}{\begin{bmatrix}2.19\\1\\\end{bmatrix}}={\begin{bmatrix}1.264\\0.707\\\end{bmatrix}}$

$x_{2}=M^{-1/2}x_{2}^{*}={\begin{bmatrix}1/{\sqrt {3}}&0\\0&1/{\sqrt {2}}\\\end{bmatrix}}{\begin{bmatrix}-0.456\\1\\\end{bmatrix}}={\begin{bmatrix}-0.263\\0.707\\\end{bmatrix}}$

So,

$x_{1}={\begin{bmatrix}1.264\\0.707\\\end{bmatrix}}$

$x_{2}={\begin{bmatrix}-0.263\\0.707\\\end{bmatrix}}$

Problem R6.2

On my honor, I have neither given nor recieved unauthorized aid in doing this assignment.

Description

We are to resolve problem 4.4/5.4 but by using the method of transforming the generalized eigenvalue problem into a standard eigenvalue problem and then proceeding in the calculations.

Solution

This problem is accomplished by using the following simple transformation:

$K^{*}=M^{-1/2}*K*M^{-1/2}$

The problem is carried out exactly the same as from report 5 until right before the eigenvectors are found. Instead, the eigenvalues and eigenvectors are found from the $K^{*}$ matrix. Once this is done, the true eigenvalues for our system are found according to:

$x=M^{-1/2}*x^{*}$

The code to solve this problem are presented below.

%Constants
p = 5000;
E = 100000000000;
A = 0.0001;
L = 0.3;
%Degree of Freedom
dof = zeros(25,5);
for i = 1:6
    j = 2*i-1;
    dof(i,:) = [i,j,j+1,j+2,j+3];
end
for i =7:12
    j = i*2+1;
    dof(i,:) = [i,j,j+1,j+2,j+3];
end
for i = 13:19
    j = (i-12)*2-1;
    dof(i,:) = [i,j,j+1,j+14,j+15];
end
for i = 20:25
    j = (i-19)*2-1;
    dof(i,:) = [i,j,j+1,j+16,j+17];
end
%coordinates
pos = zeros(2,14);
for i=1:7
    pos(:,i) = [(i-1)*L;0];
    pos(:,i+7) = [(i-1)*L;L];
end
%Connections
conn = zeros(2,25);
for i = 1:6
    conn(1,i)= i;
    conn(2,i)= i+1;
end
for i = 7:12
    conn(1,i) = i+1;
    conn(2,i) = i+2;
end
for i = 13:19
    conn(1,i) = i-12;
    conn(2,i) = i-5;
end
for i = 20:25;
    conn(1,i) = i-19;
    conn(2,i) = i-11;
end
%seperates into x and y coordinates
x = zeros(14,2);
y = zeros(14,2);
for i = 1:25
    x(i,:) = [pos(1,conn(1,i)),pos(1,conn(2,i))];
    y(i,:) = [pos(2,conn(1,i)),pos(2,conn(2,i))];
end
%Set up K and M matrix
K = zeros(28);
M = zeros(28);
for i = 1:25
    xm = x(i,2)-x(i,1);
    ym = y(i,2)-y(i,1);
    L = sqrt(xm^2+ym^2);
    l = xm/L;
    m = ym/L;
    k = E*A/L*[l^2 l*m -l^2 -l*m;l*m m^2 -l*m -m^2;-l^2 -l*m l^2 l*m;-l*m -m^2 l*m m^2;];
    m = L*A*p;
    m = [m/2 0 0 0;0 m/2 0 0;0 0 m/2 0;0 0 0 m/2];
    Dof = dof(i,2:5);
    K(Dof,Dof) = K(Dof,Dof)+k;
    M(Dof,Dof) = M(Dof,Dof)+m;
end
Msq = sqrt(M);
nMsq = inv(Msq);
%Makes an alternate K and M matrices to cancel rows and columns for boundary conditions.
Kr = K;
Msqr = Msq;
nMsqr = nMsq;

Kr([1 15 16],:) = [];
Kr(:,[1 15 16]) = [];
Msqr([1 15 16],:) = [];
Msqr(:,[1 15 16]) = [];
nMsqr([1 15 16],:) = [];
nMsqr(:,[1 15 16]) = [];
Kstar = nMsqr*Kr*nMsqr;
%Find Eigenvalue and Eigenvector
[sVec Val] = eig(Kstar);
%We now need to find the true Eigenvectors.
Vec = nMsqr*sVec;
Vec1 = zeros(25,1);
Vec2 = zeros(25,1);
Vec3 = zeros(25,1);
for i = 1:25
    Vec1(i) = Vec(i,1);
    Vec2(i) = Vec(i,2);
    Vec3(i) = Vec(i,3);
end
 
%Insert back in the values for initial conditions.
Vec1 = [0;Vec1(1:13);0;0;Vec1(14:25)];
Vec2 = [0;Vec2(1:13);0;0;Vec2(14:25)];
Vec3 = [0;Vec3(1:13);0;0;Vec3(14:25)];
 
%Add the Eigenvectors to the nodes
 
X1 = zeros(14,1);
Y1 = zeros(14,1);
X2 = zeros(14,1);
X3 = zeros(14,1);
Y2 = zeros(14,1);
Y3 = zeros(14,1);
X = zeros(14,1);
Y = zeros(14,1);
 
for i = 1:14
X1(i) = Vec1((i*2)-1,1);
Y1(i) = Vec1((i*2),1);
X(i) = pos(1,i);
Y(i) = pos(2,i);
X2(i) = Vec2((i*2)-1,1);
Y2(i) = Vec2((i*2),1);
X3(i) = Vec3((i*2)-1,1);
Y3(i) = Vec3((i*2),1);
end

References for Matlab code: Team 3 Report 4 Team 7 Report 4 Team 4 Report 5

The resulting displacements were:

X1 =

Y1 =

X2 =

Y2 =

X3 =

Y3 =

R6.3 Problem Computer reactions and compare

Problem Statement

Redo R3.1. Compute the reactions, and compare the reactions in the case of non-zero prescribed disp dofs with the reactions in the case of zero prescribed disp dofs.

Given Problem Parameters

Solution

On my honor, I have neither given nor received unauthorized aid in doing this assignment.

Given zero displacement DOFs, the following MATLAB program solves for the unknown global displacement DOF's, unknown for components (reactions), and member forces in the system.

function R6p3

F = 20000; %N
E = 206000000000; %Pa
L = 1; %m
A = .0001; %m^2
 
% displacement in meters
d3 = 0;  % =u2
d4 = 0; % =v2
d5 = 0; % =u3
d6 = 0;  % =v3

% Table 2.1 KS 2008 p.82
% Element   EA/L      i-->j    phi    l=cos(phi)  m=sin(phi)
% 1       206x10^5    1-->3   -pi/6    0.866       -0.5
% 2       206x10^5    1-->2   -pi/2      0           1
% 3       206x10^5    1-->4   -5pi/6  -0.866       -0.5
 
l1 = 0.866;
m1 = -0.5;
l2 = 0;
m2 = 1;
l3 = -0.866;
m3 = -0.5;
 
% element stiffness matrices
% E2.46 
% element 1 stiffness matrix 1-->3
k1 = [l1^2 l1*m1 0 0 -l1^2 -l1*m1 0 0;
      l1*m1 m1^2 0 0 -l1*m1 -m1^2 0 0;
      0 0 0 0 0 0 0 0;
      0 0 0 0 0 0 0 0;
      -l1^2 -l1*m1 0 0 l1^2 l1*m1 0 0;
      -l1*m1 -m1^2 0 0 l1*m1 m1^2 0 0;
      0 0 0 0 0 0 0 0;
      0 0 0 0 0 0 0 0];
  
% element 1 stiffness matrix 1-->2
k2 = [l2^2 l2*m2 -l2^2 -l2*m2 0 0 0 0;
      l2*m2 m2^2 -l2*m2 -m2^2 0 0 0 0;
      -l2^2 -l2*m2 l2^2 l2*m2 0 0 0 0;
      -l2*m2 -m2^2 l2*m2 m2^2 0 0 0 0;
      0 0 0 0 0 0 0 0;
      0 0 0 0 0 0 0 0;
      0 0 0 0 0 0 0 0;
      0 0 0 0 0 0 0 0];
  
% element 1 stiffness matrix 1-->4
k3 = [l3^2 l3*m3 0 0 0 0 -l3^2 -l3*m3;
      l3*m3 m3^2 0 0 0 0 -l3*m3 -m3^2;
      0 0 0 0 0 0 0 0;
      0 0 0 0 0 0 0 0;
      0 0 0 0 0 0 0 0;
      0 0 0 0 0 0 0 0;
      -l3^2 -l3*m3 0 0 0 0 l3^2 l3*m3;
      -l3*m3 -m3^2 0 0 0 0 l3*m3 m3^2];
 
%global stiffness matrix
K = E*A/L*(k1 + k2 + k3)
 
% Force matrix
Fpost = [F*cos(pi/4); F*sin(pi/4); 0; 0; 0; 0; 0; 0]
 
% global disp dofs
dispg = K\Fpost

% u2=v2=u3=v3=u4=v4=0, so delete rows/columns 3 through 8
Knew = 1*10^7*[3.0898 0;
              0 3.0900];
 
% displacement values u1, v1 
Fcut = [F*cos(pi/4); F*sin(pi/4)];
disp = Knew\Fcut
 
% forces in each element
P1 = E*A/L*(0.866*(d5-disp(1))-0.5*(d6-disp(2)))
P2 = E*A/L*(0*(d3-disp(1))+1*(d4-disp(2)))
P3 = E*A/L*(-0.866*(0-disp(1))-0.5*(dispg(4)-disp(2)))

stress1 = P1/A
stress2 = P2/A
stress3 = P3/A

Global Displacements

dispg =
   1.0e+12 *
       NaN
       NaN
       NaN
    3.5927
    3.7905
    6.5693
    2.3727
    3.0716

Unknown disp at node 1(m)

disp =
   1.0e-03 *
    0.4577
    0.4577

Element forces (N)

P1 =
  -3.4512e+03

P2 =
  -9.4281e+03

P3 =
   1.2879e+04

Element stresses (Pa)

stress1 =
  -3.4512e+07

stress2 =
  -9.4281e+07

stress3 =
   1.2879e+08

Verifying with Calfem and plotting

function R6p3calfem

F = 20000; %N
E = 206000000000; %Pa
L = 1; %m
A = .0001; %m^2

% Checking with CALFEM
edof = [1 1 2 5 6;
        2 1 2 3 4;
        3 1 2 7 8];
 
coord = [cos(pi/6) sin(pi/6);cos(pi/6) 1+sin(pi/6);2*cos(pi/6) 0;0 0];
dof = [1 2;3 4;5 6;7 8];
 
[ex,ey] = coordxtr(edof,coord,dof,2);
ep = [E A];
K = zeros(8);
Fo = zeros(8,1); Fo(1) = F*cos(pi/4); Fo(2) = F*sin(pi/4);
for i = 1:3
    Ke = bar2e(ex(i,:),ey(i,:),ep);
    K = assem(edof(i,:),K,Ke);
end
 
bc = [3 0; 4 0; 5 0; 6 0; 7 0; 8 0];
Q = solveq(K,Fo,bc);
ed = extract(edof,Q);
for i = 1:3
    N(i)=bar2s(ex(i,:),ey(i,:),ep,ed(i,:));
end

plotpar=[1 4 0];scale=100;
eldraw2(ex,ey);
eldisp2(ex,ey,ed,plotpar,scale);
grid on

N1 = N(1)
N2 = N(2)
N3 = N(3)

stress1c = N(1)/A
stress2c = N(2)/A
stress3c = N(3)/A

OUTPUT

N1 =
  -3.4509e+03

N2 =
  -9.4281e+03

N3 =
   1.2879e+04

stress1c =
  -3.4509e+07

stress2c =
  -9.4281e+07

stress3c =
   1.2879e+08

Original values of non-zero displacement degrees of freedom: (R3.1)
Global displacement DOF's (m)
$u_{1}=-0.005$
$v_{1}=-0.0103$
$u_{2}=0.02$
$v_{2}=-0.01$
$u_{3}=-0.03$
$v_{3}=0.05$
$u_{4}=-0.0257$
$v_{4}=0.0764$

Element Reaction Forces (N)
$P^{1}=-854900$
$P^{2}=-418180$
$P^{3}=740079$

Element Stresses (GPa)
$\sigma ^{1}=-8.5490$
$\sigma ^{2}=-4.1818$
$\sigma ^{3}=7.4008$

Problem 6.4 Deformation in 3D Space

On my honor, I have neither given nor received unauthorized aid in doing this assignment.

Problem Statement

There is a 3D truss system with applied forces. We need to optimize each beam to meet a factor of safety of 1.5.

Matlab Solution

Set up degrees of freedom and coordinates

%Constants
E = 30000000;   %Youngs Modulus
L1 = 3;         %Short lengths
L2 = 8;         %Long lengths
v = 0.3;        %poissons ratio
YS = 37000;     %Yield Strength
p = 0.00073;    %density
FS = 1.5;        %Factor of Safety        
%coordinates
pos = zeros(3,10);
pos(:,1) = [-L1/2;0;8];
pos(:,2) = [L1/2;0;8];
pos(:,3) = [-L1/2;L1/2;4];
pos(:,4) = [L1/2;L1/2;4];
pos(:,5) = [L1/2;-L1/2;4];
pos(:,6) = [-L1/2;-L1/2;4];
pos(:,7) = [-L2/2;L2/2;0];
pos(:,8) = [L2/2;L2/2;0];
pos(:,9) = [L2/2;-L2/2;0];
pos(:,10) = [-L2/2;-L2/2;0];
%Connections
conn = zeros(2,25);
conn(:,1) = [1;2];
conn(:,2) = [1;4];
conn(:,3) = [2;3];
conn(:,4) = [1;5];
conn(:,5) = [2;6];
conn(:,6) = [2;4];
conn(:,7) = [2;5];
conn(:,8) = [1;3];
conn(:,9) = [1;6];
conn(:,10) = [3;6];
conn(:,11) = [4;5];
conn(:,12) = [3;4];
conn(:,13) = [5;6];
conn(:,14) = [3;10];
conn(:,15) = [6;7];
conn(:,16) = [4;9];
conn(:,17) = [5;8];
conn(:,18) = [4;7];
conn(:,19) = [3;8];
conn(:,20) = [5;10];
conn(:,21) = [6;9];
conn(:,22) = [6;10];
conn(:,23) = [3;7];
conn(:,24) = [4;8];
conn(:,25) = [5;9];
%Degree of Freedom
dof = zeros(25,7);
D = zeros(10,3);
    %assign nodes degree of freedoms
for i = 1:10
    j = (i-1)*2+i;
    D(i,:) = [j,j+1,j+2];
end
    %Assign members their DOF's
for i = 1:25
    dof(i,:) = [i,D(conn(1,i)',:),D(conn(2,i)',:)];
end
%seperates into x and y coordinates
x = zeros(25,2);
y = zeros(25,2);
z = zeros(25,2);
for i = 1:25
    x(i,:) = [pos(1,conn(1,i)),pos(1,conn(2,i))];
    y(i,:) = [pos(2,conn(1,i)),pos(2,conn(2,i))];
    z(i,:) = [pos(3,conn(1,i)),pos(3,conn(2,i))];
end

Set up K matrix to be used for calculations

%Set up K and M matrix
K = zeros(30);
M = zeros(30);

A = zeros(25,1);
for i = 1:25
    A(i) = pi()*(2/2)^2;   %Area of all members
end
for i = 1:25
    xm = x(i,2)-x(i,1);
    ym = y(i,2)-y(i,1);
    zm = z(i,2)-z(i,1);
    L = sqrt(xm^2+ym^2+zm^2);
    l = xm/L;
    m = ym/L;
    n = zm/L;
    k = E*A(i)/L*[l^2 l*m l*n -l^2 -l*m -l*n;l*m m^2 m*n -l*m -m^2 -m*n;l*n m*n n^2 -l*n -m*n -n^2;-l^2 -l*m -l*n l^2 l*m l*n;-l*m -m^2 -m*n l*m m^2 m*n;-l*n -m*n -n^2 l*n m*n n^2];
    m = L*A(i)*p;
    m = [m/2 0 0 0 0 0;0 m/2 0 0 0 0;0 0 m/2 0 0 0;0 0 0 m/2 0 0;0 0 0 0 m/2 0;0 0 0 0 0 m/2];
    Dof = dof(i,2:7);
    K(Dof,Dof) = K(Dof,Dof)+k;
    M(Dof,Dof) = M(Dof,Dof)+m;
end

Reduce matrices and make initial conditions

%Makes an alternate K and M matrix to calncel rows and columns for boundary
%conditions.
Kr = K;
Mr = M;
Kr((19:30),:) = [];
Kr(:,(19:30)) = [];
Mr((19:30),:) = [];
Mr(:,(19:30)) = [];

%Applied Forces
F = zeros(18,1);
F(2) = 60000;
F(5) = 60000;

Determine the deformation of each DOF

d = Kr\F;
d = [d;zeros(12,1)];

Set up new coordinates and determine stress and strain

posn = zeros(3,10);
%new position vectors
for i = 1:10
    j = i*3;
    posn(1,i) = pos(1,i) + d(j-2);
    posn(2,i) = pos(2,i) + d(j-1);
    posn(3,i) = pos(3,i) + d(j);
end

xn = zeros(25,2);
yn = zeros(25,2);
zn = zeros(25,2);
%Put in new coordinates
for i = 1:25
    xn(i,:) = [posn(1,conn(1,i)),posn(1,conn(2,i))];
    yn(i,:) = [posn(2,conn(1,i)),posn(2,conn(2,i))];
    zn(i,:) = [posn(3,conn(1,i)),posn(3,conn(2,i))];
end

%Finding stress and FOS
e = zeros(25,1);
o = zeros(25,1);
for i = 1:25
    xm = x(i,2)-x(i,1);
    ym = y(i,2)-y(i,1);
    zm = z(i,2)-z(i,1);
    L = sqrt(xm^2+ym^2+zm^2);
    xl = xn(i,2)-xn(i,1);
    yl = yn(i,2)-yn(i,1);
    zl = zn(i,2)-zn(i,1);
    Ll = sqrt(xl^2+yl^2+zl^2);
    e(i) = (Ll-L)/L;                %Strain
    o(i) = e(i)*E;                  %Stress
end

Determine factor of safety and reduce area

FOS = zeros(25,1);
on = 1.5*YS;
for i = 1:25
    A(i) = A(i)*abs(o(i))/on;
    FOS(i) = YS/abs(o(i));
    if A(i) <= pi()*(0.1/2)^2
       A(i) = pi()*(0.1/2)^2;
    elseif A(i) >= pi()*(2.5/2)^2
        A(i) = pi()*(2.5/2)^2;
    end
    
end

Conclusion

The final area of each member was able to be reduced to its minimum of 0.1 inches and stay above a factor of safety of 1.5. Final stresses are in psi:

13.94
-8487.15
-8487.15
8611.63
8611.63
-12871.54
13045.99
-12871.54
13045.99
63.42
63.42
788.95
-778.48
-5171.02
5174.49
-5171.02
5174.49
-7787.74
-7787.74
7792.39
7792.39
14680.46
-14679.76
-14679.76
14680.46

CALFEM Verification

The Matlab calculations were confirmed using the CALFEM toolbox in Matlab.

The following presents the constants used and options for different designs

E = 30000000;   %modulus
p = 0.00073;    %density
L1 = 3;         %Short lengths
L2 = 8;         %Long lengths
v = 0.3;        %poissons ratio
YS = 37000;     %Yield Strength
FS = 1.5;        %Factor of Safety  
A = pi()*(2/2)^2;
A = 0.1 %used if reducing area to 0.1 in
ep=[E A p*A];

This Edof matrix uses column 1 as the as the element number. The next three columns are the DOFs for the first node and the next three columns are for the second node since this is a three dimensional problem.

  Edof =[1     1     2     3     4     5     6
     2     1     2     3    10    11    12
     3     4     5     6     7     8     9
     4     1     2     3    13    14    15
     5     4     5     6    16    17    18
     6     4     5     6    10    11    12
     7     4     5     6    13    14    15
     8     1     2     3     7     8     9
     9     1     2     3    16    17    18
    10     7     8     9    16    17    18
    11    10    11    12    13    14    15
    12     7     8     9    10    11    12
    13    13    14    15    16    17    18
    14     7     8     9    28    29    30
    15    16    17    18    19    20    21
    16    10    11    12    25    26    27
    17    13    14    15    22    23    24
    18    10    11    12    19    20    21
    19     7     8     9    22    23    24
    20    13    14    15    28    29    30
    21    16    17    18    25    26    27
    22    16    17    18    28    29    30
    23     7     8     9    19    20    21
    24    10    11    12    22    23    24
    25    13    14    15    25    26    27];

Coord contains the x, y, and z coordinates for each node.

Coord =[-1.5000         0    8.0000
    1.5000         0    8.0000
   -1.5000    1.5000    4.0000
    1.5000    1.5000    4.0000
    1.5000   -1.5000    4.0000
   -1.5000   -1.5000    4.0000
   -4.0000    4.0000         0
    4.0000    4.0000         0
    4.0000   -4.0000         0
   -4.0000   -4.0000         0];

Dof =[1     2     3
     4     5     6
     7     8     9
    10    11    12
    13    14    15
    16    17    18
    19    20    21
    22    23    24
    25    26    27
    28    29    30];

The bar3e is used to make the stiffness matrix for a 3D system. The bar3s is used to find the member forces in a 3D system. One can see that the 3 denotes the dimension of the system being observed. The stresses can be found by dividing the forces by the areas.

Ex, Ey, Ez]=coordxtr(Edof, Coord, Dof, 2);

K=zeros(30);F=zeros(30,1);F(1)=60,000; F(2)=60,000;

for i=1:25
    Ke=bar3e(Ex(i,:),Ey(i,:),Ez(i,:),ep);
    K=assem(Edof(i,:),K,Ke);
end

bc=[7 0;8 0;9 0;10 0;];

Q=solveq(K,F,bc);

Ed=extract(Edof,Q);

for i=1:25
    N(i)=bar3s(Ex(i,:),Ey(i,:),Ez(i,:),ep,Ed(i,:));
end

S=N/A

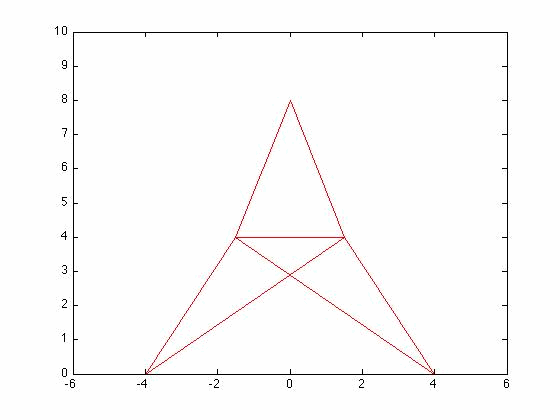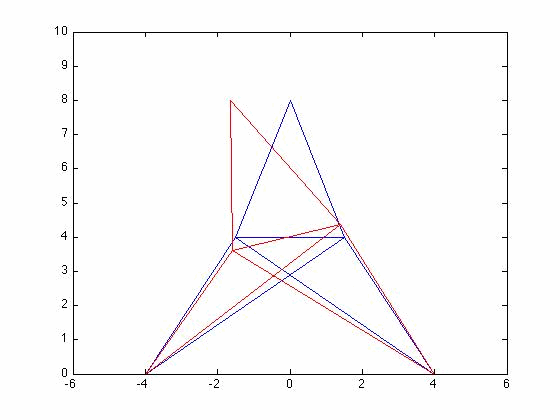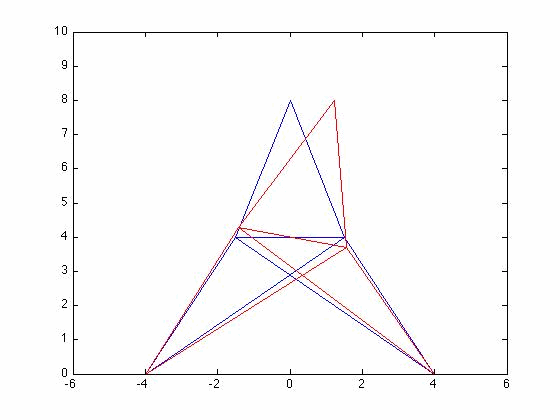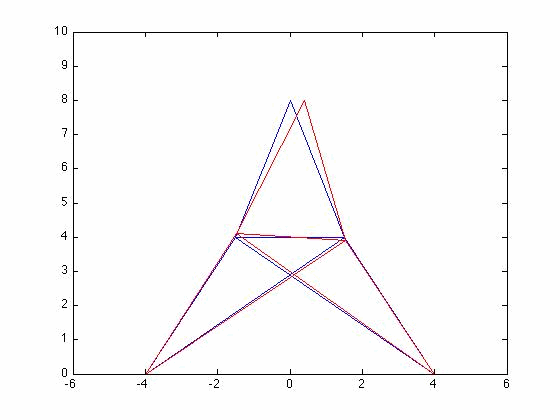
Problem 6.5 3d Mode Shapes

On my honor, I have neither given nor received unauthorized aid in doing this assignment.

Problem Statement

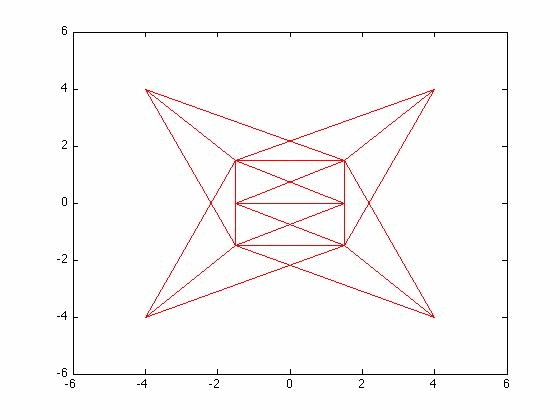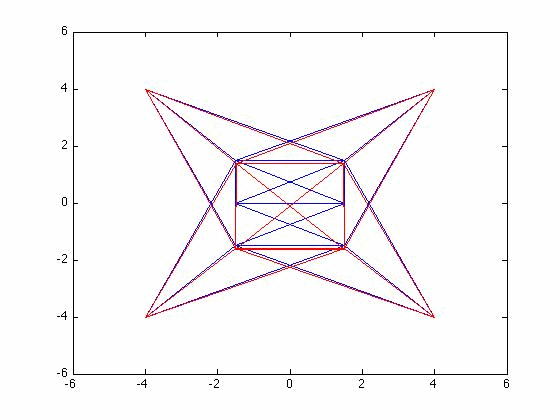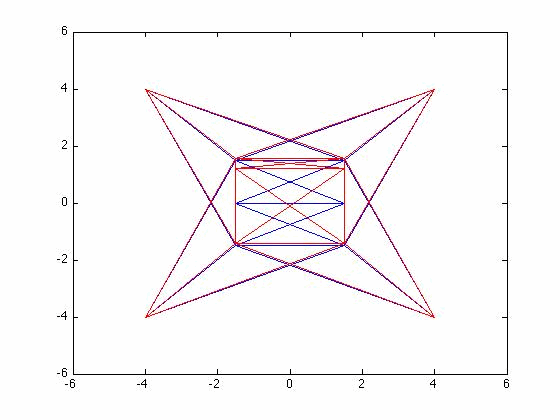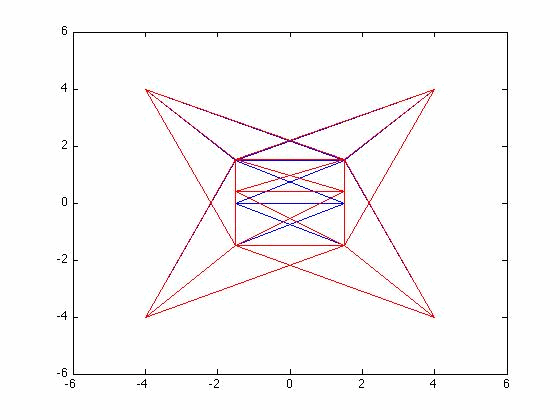
Determine the first 3 mode shapes of the 3D truss system from problem 6.4

Solution

The set up of the problem was the same as problem 6.4. The eigenvalues can be seen below.

Matlab code

%Makes an alternate K and M matrix to calncel rows and columns for boundary
%conditions.
Kr = K;
Mr = M;
Kr((19:30),:) = [];
Kr(:,(19:30)) = [];
Mr((19:30),:) = [];
Mr(:,(19:30)) = [];

%Find Eigenvalue and Eigenvector
[Vec Val] = eig(Kr,Mr);
Vec1 = zeros(18,1);
Vec2 = zeros(18,1);
Vec3 = zeros(18,1);
for i = 1:18
    Vec1(i) = Vec(i,1);
    Vec2(i) = Vec(i,2);
    Vec3(i) = Vec(i,3);
end

%Insert back in the values for initial conditions.
Vec1 = [Vec1;zeros(12,1)];
Vec2 = [Vec2;zeros(12,1)];
Vec3 = [Vec3;zeros(12,1)];


%Add the Eigenvectors to the nodes
X1 = zeros(10,1);
Y1 = zeros(10,1);
Z1 = zeros(10,1);
X2 = zeros(10,1);
Y2 = zeros(10,1);
Z2 = zeros(10,1);
X3 = zeros(10,1);
Y3 = zeros(10,1);
Z3 = zeros(10,1);
X = zeros(10,1);
Y = zeros(10,1);
Z = zeros(10,1);
for i = 1:10
X1(i) = Vec1((i*3)-2,1);
Y1(i) = Vec1((i*3)-1,1);
Z1(i) = Vec1((i*3),1);
X(i) = pos(1,i);
Y(i) = pos(2,i);
Z(i) = pos(3,i);
X2(i) = Vec2((i*3)-2,1);
Y2(i) = Vec2((i*3)-1,1);
Z2(i) = Vec2((i*3),1);
X3(i) = Vec3((i*3)-2,1);
Y3(i) = Vec3((i*3)-1,1);
Z3(i) = Vec3((i*3),1);
end
X1 = X+X1;
Y1 = Y+Y1;
Z1 = Z+Z1;
X2 = X+X2;
Y2 = Y+Y2;
Z2 = Z+Z2;
X3 = X+X3;
Y3 = Y+Y3;
Z3 = Z+Z3;

Code used to plot the graphs

%plot origional shape
for i = 1:25
xc = [X(conn(1,i)),X(conn(2,i))];
yc = [Y(conn(1,i)),Y(conn(2,i))];
%zc = [Z(conn(1,i)),Z(conn(2,i))];
plot(xc,yc)
axis([-6 6 -6 6])
hold on
end

%plot mode 1
for i = 1:25
xc = [X1(conn(1,i)),X1(conn(2,i))];
yc = [Y1(conn(1,i)),Y1(conn(2,i))];
%zc = [Z1(conn(1,i)),Z1(conn(2,i))];
plot(xc,yc,'r')
hold on
end

%plot mode 2
for i = 1:25
xc = [X2(conn(1,i)),X2(conn(2,i))];
yc = [Y2(conn(1,i)),Y2(conn(2,i))];
zc = [Z2(conn(1,i)),Z2(conn(2,i))];
plot(xc,yc,'r')
hold on
end

%plot mode 3
for i = 1:25
xc = [X3(conn(1,i)),X3(conn(2,i))];
yc = [Y3(conn(1,i)),Y3(conn(2,i))];
%zc = [Z3(conn(1,i)),Z3(conn(2,i))];
plot(xc,yc,'r')
hold on
end

Gif's of mode shapes

Mode 1

Front View

Top View

Mode 2

Front View

Top View

Mode 3

Diagonal View

Top View

Table of Assignments R6

Problem Assignments R5
Problem #	Solved&Typed by	Reviewed by
1	Bryan Tobin, Chad Colocar	All
2	David Bonner, Vernon Babich	All
3	Chad Colocar, Bryan Tobin	All
4	Vernon Babich, Tyler Wulterkens	All
5	Tyler Wulterkens, David Bonner	All