University of Florida/Eml4507/s13.team4ever.R5

Problem R5.1

On my honor, I have neither given nor recieved unauthorized aid in doing this assignment.

Description

We are to solve, by hand, the generalized eigenvalue for the mass-spring-damper system on p. 53-13 using the following data for the masses and stiffness coefficients:

$m_{1}=3$

$m_{2}=2$

$k_{1}=10$

$k_{2}=20$

$k_{3}=15$

We are then to compare this result with those obtained using CALFEM. Finally, we are to verify the mass-orthogonality of the eigenvectors.

Given:

We are given that for a generalized eigenvalue problem:

$K\phi =\lambda M\phi$

We also know that:

$M={\begin{bmatrix}m_{1}&0\\0&m_{2}\\\end{bmatrix}}$ and $K={\begin{bmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{2}+k_{3}\\\end{bmatrix}}$

Therefore, we have:

$M={\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}$ and $K={\begin{bmatrix}30&-20\\-20&35\\\end{bmatrix}}$

Solution:

The first step would be to find an eigenvalue, $\lambda$ that satifies:

$K\phi =\lambda M\phi$

To do this, we must find an eigenvalue that satifies:

$det(K-\lambda M)=0$

We then have:

$det({\begin{bmatrix}30-3\lambda &-20\\-20&35-2\lambda \\\end{bmatrix}}=0$)

This gives us

$(30-3\lambda )(35-2\lambda )+400=0$

$6\lambda ^{2}-165\lambda +650=0$

Solving this equation using the quadratic equation gives us eigenvalues of:

$\lambda _{1,2}=13.75\pm 8.985$

$\lambda _{1}=4.765$

$\lambda _{2}=22.735$

We will first take the lowest eigenvalue. We'll now try to find the corresponding eigenvector. Plugging this eigenvalue into the equaiton

$K\phi =\lambda M\phi$

$K\phi -\lambda M\phi =0$

$(K-\lambda M)\phi =0$

$(K-4.765M)\phi =0$

We need to find a value of $\phi$ that satisfies the above equation.

${\begin{bmatrix}30-(3)(4.765)&-20\\-20&35-(2)(4.765)\\\end{bmatrix}}{\begin{bmatrix}\phi _{1}\\\phi _{2}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

${\begin{bmatrix}15.705&-20\\-20&25.47\\\end{bmatrix}}{\begin{bmatrix}\phi _{1}\\\phi _{2}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

Augmenting the right hand matrix onto the left hand matrix and putting this in row reduced echelon form, we obtain,

${\begin{bmatrix}1&-1.273&0\\0&0&0\\\end{bmatrix}}$

This means that the corresponding eigenvector is:

$\phi _{1}={\begin{bmatrix}1.273\\1\\\end{bmatrix}}$

We will now take the higher eigenvalue. We'll now try to find the corresponding eigenvector. Plugging this eigenvalue into the equaiton

$K\phi =\lambda M\phi$

$K\phi -\lambda M\phi =0$

$(K-\lambda M)\phi =0$

$(K-22.735M)\phi =0$

We need to find a value of $\phi$ that satisfies the above equation.

${\begin{bmatrix}30-(3)(22.735)&-20\\-20&35-(2)(22.735)\\\end{bmatrix}}{\begin{bmatrix}\phi _{1}\\\phi _{2}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

${\begin{bmatrix}-38.205&-20\\-20&-10.47\\\end{bmatrix}}{\begin{bmatrix}\phi _{1}\\\phi _{2}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

Augmenting the right hand matrix onto the left hand matrix and putting this in row reduced echelon form, we obtain,

${\begin{bmatrix}1&0.5234&0\\0&0&0\\\end{bmatrix}}$

This means that the corresponding eigenvector is:

$\phi _{2}={\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}$

We will now verify the mass orthogonality of the eigenvectors. To do this, we need to show that

$\phi _{i}^{T}M\phi _{j}=0$ for i not equal to j. For our case, we have:

$\phi _{1}^{T}={\begin{bmatrix}1.273&1\\\end{bmatrix}}$

$M={\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}$ and

$\phi _{2}={\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}$

We have then that

$\phi _{i}^{T}M\phi _{j}={\begin{bmatrix}1.273&1\\\end{bmatrix}}{\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}{\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}=0$

Thus verifying the mass-orthogonality of the eigenvectors.

Using our own code from Report 3, we can compare this with CALFEM:

d0=[-1,2];
v0=[0,0];
alpha=1/4; delta=1/2;
nsnap=100;
m1=3;
m2=2;
alpha=1/4; delta=1/2;
d0=[-1,2];
v0=[0,0];
k1=10;
k2=20;
k3=15;
c1=1/2;
c2=1/4;
c3=1/3;
M=[m1,0;0,m2];
C=[(c1+c2),-c2;-c2,(c2+c3)];
K=[(k1+k2),-k2;-k2,(k2+k3)];
[L]=eigen(K,M);
w1=sqrt(L(1));
T1=(2*pi)/w1;
dt=T1/10;
T=[0:dt:5*T1];
Dsnap=step2x(K,C,M,d0,v0,ip,f,pdisp);

EDU>> L
L =
    4.7651
   22.7349
EDU>> w1
w1 =
    2.1829
EDU>> T1
T1 =
    0.3473
EDU>> dt
dt =
    0.0347

R5.2

Length of members 2-3 and 4-5 (truss height):
$L_{23}=L_{45}=1$

Length of members 1-2, 2-4, 4-6 (truss length):
$L_{12}=L_{24}=L_{46}=1$

Area of cross section:
$A=1/2$

Young's modulus:
$E=5$

Mass Density:
$\rho =2$

Part One:
Solve the generalized eigenvalue problem of the above truss. Display the results for the lowest 3 eigenpairs. Plot the mode shapes.

Part Two:
Consider the same truss, but with 2 missing braces:

Solve the generalized eigenvalue for this truss, and plot the mode shapes.

Solution

On my honor, I have neither given nor received unauthorized aid in doing this problem.

function R5p2
 
% Part One
 
E = 5;
p = 2;  %kg/m3a
A = 0.5;  %m2
L = 1;   %m
 
h = p*A*L;
v = h;
d = (sqrt((L^2)+(L^2)))*A*p;
 
m = [(h/2)+(d/2);(h/2)+(d/2);
    (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
    (h/2)+(d/2)+(d/2)+(v/2);(h/2)+(d/2)+(d/2)+(v/2);
    (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
    (h/2)+(d/2)+(d/2)+(v/2);(h/2)+(d/2)+(d/2)+(v/2);
    (h/2)+(d/2);(h/2)+(d/2)];
 
M = diag(m);
 
Coord = [0 0;1 0;1 1;2 0;2 1;3 0];
Dof = [1 2;3 4;5 6;7 8;9 10;11 12];
Edof = [1 1 2 3 4;2 1 2 5 6;3 3 4 5 6;4 5 6 9 10;5 5 6 7 8;
    6 3 4 9 10;7 3 4 7 8;8 7 8 9 10;9 9 10 11 12;10 7 8 11 12];
bc = [1;2;12];
 
[Ex,Ey] = coordxtr(Edof,Coord,Dof,2)
K = zeros(12);
F = zeros(12,1);
ep = [E A];
 
for i=1:10
    Ke = bar2e(Ex(i,:),Ey(i,:),ep);
    K = assem(Edof(i,:),K,Ke);
end
 
[L,X] = eigen(K,M,bc);
 
eigval = L;
eigvect = X;
 
j1eig = eigval(1)
j1eigvx = eigvect(:,1)
j1eigvy = eigvect(:,2)
 
j2eig = eigval(2)
j2eigvx = eigvect(:,3)
j2eigvy = eigvect(:,4)
 
j3eig = eigval(3)
j3eigvx = eigvect(:,5)
j3eigvy = eigvect(:,6)
 
plotpar = [1 4 0];
scale = .5;
eldraw2(Ex,Ey);
 
for j=1:3
    clear plot
    ed = extract(Edof,X(:,j));
    P = eldisp2(Ex,Ey,ed,plotpar,scale);
    W(j) = getframe;
    drawnow
end

Three lowest eigenpairs

j1eig =
    0.0890

j1eigvx =
         0
         0
   -0.0938
    0.2910
   -0.1706
    0.2804
   -0.1679
    0.2946
   -0.1131
    0.2756
   -0.2330
         0

j1eigvy =
         0
         0
   -0.1713
   -0.2076
   -0.2639
   -0.1197
   -0.2637
   -0.1637
   -0.3443
   -0.1391
   -0.2757
         0

j2eig =
    0.2779

j2eigvx = 
         0
         0
   -0.1902
    0.2970
    0.1621
    0.2185
   -0.2188
   -0.3370
    0.1475
   -0.2327
   -0.0779
         0

j2eigvy =
         0
         0
    0.0382
    0.1640
   -0.2909
    0.1947
    0.2640
   -0.0109
   -0.1970
   -0.2662
    0.4295
         0

j3eig =
    0.5582
  
j3eigvx =
         0
         0
    0.2733
    0.2621
   -0.0575
   -0.1395
    0.1216
   -0.3929
   -0.1489
    0.2738
   -0.1309
         0

j3eigvy = 
         0
         0
    0.3282
   -0.2744
    0.1584
    0.4169
    0.0086
   -0.0685
   -0.1419
   -0.0349
   -0.2114
         0
  

Mode Shape 1

Mode Shape 2

Mode Shape 3

%  Part Two
 
Coord = [0 0;1 0;1 1;2 0;2 1;3 0];
Dof = [1 2;3 4;5 6;7 8;9 10;11 12];
Edof = [1 1 2 3 4;2 1 2 5 6;3 3 4 5 6;4 5 6 9 10;5 9 10 11 12;
    6 7 8 11 12;7 3 4 7 8;8 7 8 9 10];
 
[Ex,Ey] = coordxtr(Edof,Coord,Dof,2);
K = zeros(12);
bc = [1;2;12];
ep = [E A];
 
for i=1:8
    Ke = bar2e(Ex(i,:),Ey(i,:),ep);
    K = assem(Edof(i,:),K,Ke);
end
 
[L,X] = eigen(K,M,bc);
 
eigval = L;
eigvect = X;
 
j1eig = eigval(1)
j1eigvx = eigvect(:,1)
j1eigvy = eigvect(:,2)
 
j2eig = eigval(2)
j2eigvx = eigvect(:,3)
j2eigvy = eigvect(:,4)
 
j3eig = eigval(3)
j3eigvx = eigvect(:,5)
j3eigvy = eigvect(:,6)
 
plotpar = [1 4 0];
scale = .5;
eldraw2(Ex,Ey);
 
for j=3
    clear plot
    ed = extract(Edof,X(:,j));
    P = eldisp2(Ex,Ey,ed,plotpar,scale);
    W(j) = getframe;
    drawnow
end

Three lower eigen pairs

j1eig =
   5.5511e-17

j1eigvx =
         0
         0
    0.0000
    0.2666
   -0.2666
    0.2666
    0.0000
   -0.2666
   -0.2666
   -0.2666
    0.0000
         0

j1eigvy =
         0
         0
    0.0872
   -0.2534
    0.1188
   -0.2333
    0.1675
   -0.3552
    0.0680
   -0.3270
    0.2344
         0

j2eig =
    0.0902

j2eigvx =
         0
         0
   -0.1544
   -0.3189
   -0.2063
   -0.2326
   -0.2669
   -0.0106
   -0.3004
   -0.0077
   -0.3073
         0

j2eigvy =
         0
         0
   -0.2636
    0.1334
    0.2701
    0.0540
   -0.3702
   -0.2297
    0.2087
   -0.0929
   -0.2564
         0

j3eig =
    0.3066

j3eigvx =
         0
         0
   -0.1315
   -0.2916
   -0.3174
    0.2561
   -0.0160
   -0.1685
    0.3129
    0.1479
    0.1295
         0

j3eigvy =
         0
         0
   -0.3520
   -0.0374
   -0.0322
    0.0346
   -0.0265
    0.3638
    0.0364
   -0.3364
    0.3501
         0

Mode Shape 1

Mode Shape 2

Mode Shape 3

Problem R.5.3

Honor Pledge:

On my honor I have neither given nor received unauthorized aid in doing this problem.

Problem Description:

We are tasked with finding the eigenvector $x_{1}$ corresponding to the eigenvalue $\lambda _{1}$ for the same system as described in R4.1. We must also plot the mode shapes and compare with those from R4.1. Lastly we are tasked with creating an animation for each mode shape.

Given:

from Fead.s13.sec53b(4).djvu:

$K={\begin{bmatrix}3&-2\\-2&5\\\end{bmatrix}}$

$\gamma _{1}=4-{\sqrt {5}}$

$\gamma _{2}=4+{\sqrt {5}}$

and, from R4.1

$X_{2}={\begin{bmatrix}-0.618\\1\\\end{bmatrix}}$

Solution:

${\begin{bmatrix}K-\gamma _{1}*I\\\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

So,

${\begin{bmatrix}-1+{\sqrt {5}}&-2\\-2&1+{\sqrt {5}}\\\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\\end{bmatrix}}$

Combining and reducing to row echelon form.
${\begin{bmatrix}1&-0.618&0\\0&0&0\\\end{bmatrix}}$

we may set $x_{1}=1$ and obtain:

$X_{1}={\begin{bmatrix}1\\1.618\\\end{bmatrix}}$

Proving that they are orthogonal by ensuring the dot product between the two is zero:
$X_{1}$ ${\dot {}}$ $X_{2}=(1)(-0.618)+(1)(1.618)=0$

The eigenvalue corresponding to this eigenvector is the smallest possible and therefore this must be a fundamental mode unlike the one from R.4.1.

Mode shape plotted in picture below as well as Matlab graph showing the mode 1 in blue and mode 2 in green. The oscillation moves from zero out to the displacement for each respective mass. It can be seen that the oscillation for mode 2 is indeed fundamental as both masses move in the same direction.
Picture is adapted from Fead.s13.sec53b(4).djvu p.53-16.

Problem 5.4 Eigenvalues and Eigenvectors for Mode Shape

On my honor, I have neither given nor recieved unauthorized aid in doing this assignment.

Problem Statement

Assume the mass density to be 5,000 $kg/m^{3}$. Contruct the diagonal mass matrix and find the eigenpairs. With this, design a matlab and calfem program to determine the deformation shape.

Matlab Solution

%Constants
p = 5000;
E = 100000000000;
A = 0.0001;
L = 0.3;
%Degree of Freedom
dof = zeros(25,5);
for i = 1:6
    j = 2*i-1;
    dof(i,:) = [i,j,j+1,j+2,j+3];
end
for i =7:12
    j = i*2+1;
    dof(i,:) = [i,j,j+1,j+2,j+3];
end
for i = 13:19
    j = (i-12)*2-1;
    dof(i,:) = [i,j,j+1,j+14,j+15];
end
for i = 20:25
    j = (i-19)*2-1;
    dof(i,:) = [i,j,j+1,j+16,j+17];
end
%coordinates
pos = zeros(2,14);
for i=1:7
    pos(:,i) = [(i-1)*L;0];
    pos(:,i+7) = [(i-1)*L;L];
end
%Connections
conn = zeros(2,25);
for i = 1:6
    conn(1,i)= i;
    conn(2,i)= i+1;
end
for i = 7:12
    conn(1,i) = i+1;
    conn(2,i) = i+2;
end
for i = 13:19
    conn(1,i) = i-12;
    conn(2,i) = i-5;
end
for i = 20:25;
    conn(1,i) = i-19;
    conn(2,i) = i-11;
end
%seperates into x and y coordinates
x = zeros(14,2);
y = zeros(14,2);
for i = 1:25
    x(i,:) = [pos(1,conn(1,i)),pos(1,conn(2,i))];
    y(i,:) = [pos(2,conn(1,i)),pos(2,conn(2,i))];
end
%Set up K and M matrix
K = zeros(28);
M = zeros(28);
for i = 1:25
    xm = x(i,2)-x(i,1);
    ym = y(i,2)-y(i,1);
    L = sqrt(xm^2+ym^2);
    l = xm/L;
    m = ym/L;
    k = E*A/L*[l^2 l*m -l^2 -l*m;l*m m^2 -l*m -m^2;-l^2 -l*m l^2 l*m;-l*m -m^2 l*m m^2;];
    m = L*A*p;
    m = [m/2 0 0 0;0 m/2 0 0;0 0 m/2 0;0 0 0 m/2];
    Dof = dof(i,2:5);
    K(Dof,Dof) = K(Dof,Dof)+k;
    M(Dof,Dof) = M(Dof,Dof)+m;
end

%Makes an alternate K and M matrix to calncel rows and columns for boundary
%conditions.
Kr = K;
Mr = M;
Kr([1 15 16],:) = [];
Kr(:,[1 15 16]) = [];
Mr([1 15 16],:) = [];
Mr(:,[1 15 16]) = [];
%Find Eigenvalue and Eigenvector
[Vec Val] = eig(Kr,Mr);
 
Vec1 = zeros(25,1);
Vec2 = zeros(25,1);
Vec3 = zeros(25,1);
for i = 1:25
    Vec1(i) = Vec(i,1);
    Vec2(i) = Vec(i,2);
    Vec3(i) = Vec(i,3);
end
 
%Insert back in the values for initial conditions.
Vec1 = [0;Vec1(1:13);0;0;Vec1(14:25)];
Vec2 = [0;Vec2(1:13);0;0;Vec2(14:25)];
Vec3 = [0;Vec3(1:13);0;0;Vec3(14:25)];

%Add the Eigenvectors to the nodes

X1 = zeros(14,1);
Y1 = zeros(14,1);
X2 = zeros(14,1);
X3 = zeros(14,1);
Y2 = zeros(14,1);
Y3 = zeros(14,1);
X = zeros(14,1);
Y = zeros(14,1);

for i = 1:14
X1(i) = Vec1((i*2)-1,1);
Y1(i) = Vec1((i*2),1);
X(i) = pos(1,i);
Y(i) = pos(2,i);
X2(i) = Vec2((i*2)-1,1);
Y2(i) = Vec2((i*2),1);
X3(i) = Vec3((i*2)-1,1);
Y3(i) = Vec3((i*2),1);
end

%plot origional shape
for i = 1:25
xc = [X(conn(1,i)),X(conn(2,i))];
yc = [Y(conn(1,i)),Y(conn(2,i))];
axis([0 2 -1 1])
plot(xc,yc)
hold on
end

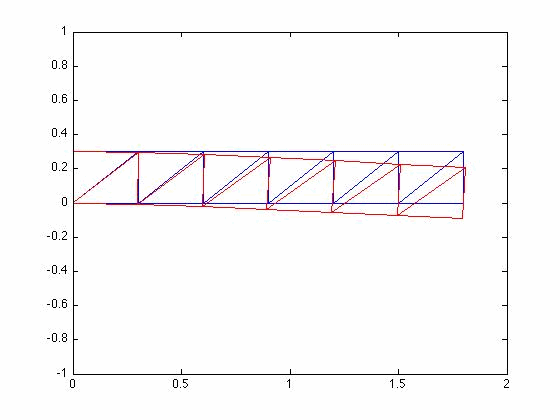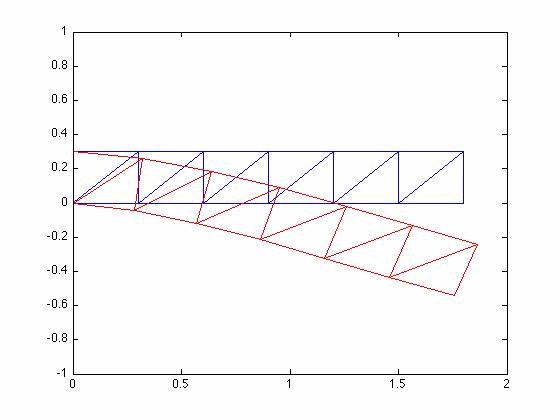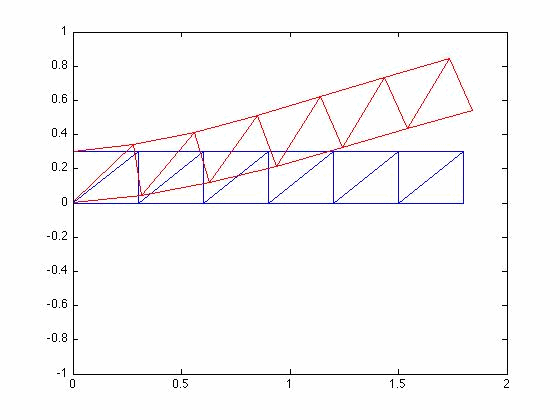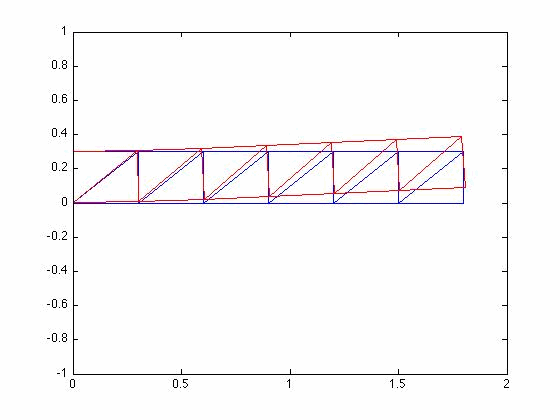
X1 = X+-0.1*X1;
Y1 = Y+-0.1*Y1;

%plot mode 1
for i = 1:25
xc = [X1(conn(1,i)),X1(conn(2,i))];
yc = [Y1(conn(1,i)),Y1(conn(2,i))];
axis([0 2 -1 1])
plot(xc,yc,'r')
hold on
end


X2 = X+X2;
Y2 = Y+Y2;
X3 = X-0.9*X3;
Y3 = Y-0.9*Y3;

%plot mode 2
for i = 1:25
xc = [X2(conn(1,i)),X2(conn(2,i))];
yc = [Y2(conn(1,i)),Y2(conn(2,i))];
axis([0 2 -1 1])
plot(xc,yc,'r')
hold on
end

%plot mode 3
for i = 1:25
xc = [X3(conn(1,i)),X3(conn(2,i))];
yc = [Y3(conn(1,i)),Y3(conn(2,i))];
axis([0 2 -1 1])
plot(xc,yc,'r')
hold on
end

References for Matlab code: Team 3 Report 4 Team 7 Report 4

Mode Shapes

CALFEM Solution

function R4p4

 p = 5000;  %kg/m3
 A = 0.01;  %m2
 L = 0.3;   %m
 
 h = p*A*L;
 v = h;
 d = (sqrt((L^2)+(L^2)))*A*p;
 
 m = [(h/2)+(d/2)+(v/2);(h/2)+(d/2)+(v/2);
     (h/2)+(v/2);(h/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(h/2)+(d/2)+(v/2);(h/2)+(h/2)+(d/2)+(v/2);
     (h/2)+(v/2);(h/2)+(v/2);
     (h/2)+(d/2)+(v/2);(h/2)+(d/2)+(v/2)];
 
 M = diag(m);
 
 Coord = [0 0;0 0.3;0.3 0;0.3 0.3;0.6 0;
     0.6 0.3;0.9 0;0.9 0.3;1.2 0;1.2 0.3;
     1.5 0;1.5 0.3;1.8 0;1.8 0.3];
 Dof = [1 2;3 4;5 6;7 8;9 10;1 12;13 14;15 16;
     17 18;19 20;21 22;23 24;25 26;27 28];
 Edof = [1 1 2 5 6;2 5 6 9 10;3 9 10 13 14;4 13 14 17 18;5 17 18 21 22;
     6 21 22 25 26;7 3 4 7 8;8 7 8 11 12;9 11 12 15 16;10 15 16 19 20;
     11 19 20 23 24;12 23 24 27 28;13 1 2 3 4;14 5 6 7 8;15 9 10 11 12;
     16 13 14 15 16;17 17 18 19 20;18 21 22 23 24;19 25 26 27 28;20 1 2 7 8;
     21 5 6 11 12;22 9 10 15 16;23 13 14 19 20;24 17 18 23 24;25 21 22 27 28];
 
 [Ex,Ey] = coordxtr(Edof,Coord,Dof,2);
 K = zeros(28);
 ep = [100000000000 0.01];
 
 for i=1:25
     Ke = bar2e(Ex(i,:),Ey(i,:),ep);
     K = assem(Edof(i,:),K,Ke);
 end
 
 [L,X] = eigen(K,M);
 
 eigval = L;
 eigvect = X;

Three lowest eigenvalues and eigenvectors

j1eig = eigval(1)
j1eigvx = eigvect(:,1)
j1eigvy = eigvect(:,2)

j2eig = eigval(2)
j2eigvx = eigvect(:,3)
j2eigvy = eigvect(:,4)

j3eig = eigval(3)
j3eigvx = eigvect(:,5)
j3eigvy = eigvect(:,6)


j1eig =
 -4.1672e-08

j1eigvx =
  -0.0018
   0.0853
   0.0136
   0.0853
  -0.0018
   0.0699
   0.0136
   0.0699
  -0.0018
   0.0545
   0.0136
   0.0545
  -0.0018
   0.0391
   0.0136
   0.0391
  -0.0018
   0.0238
   0.0136
   0.0238
  -0.0018
   0.0084
   0.0136
   0.0084
  -0.0018
  -0.0070
   0.0136
  -0.0070

j1eigvy =
  -0.0485
   0.0068
  -0.0488
   0.0068
  -0.0485
   0.0071
  -0.0488
   0.0071
  -0.0485
   0.0074
  -0.0488
   0.0074
  -0.0485
   0.0077
  -0.0488
   0.0077
  -0.0485
   0.0080
  -0.0488
   0.0080
  -0.0485
   0.0083
  -0.0488
   0.0083
  -0.0485
   0.0086
  -0.0488
   0.0086

j2eig =
 -1.0740e-08

j2eigvx =
   0.0155
  -0.0334
  -0.0053
  -0.0334
   0.0155
  -0.0127
  -0.0053
  -0.0127
   0.0155
   0.0081
  -0.0053
   0.0081
   0.0155
   0.0289
  -0.0053
   0.0289
   0.0155
   0.0496
  -0.0053
   0.0496
   0.0155
   0.0704
  -0.0053
   0.0704
   0.0155
   0.0912
  -0.0053
   0.0912

j2eigvy =
  -0.0242
   0.0747
   0.0200
   0.0761
  -0.0197
   0.0156
   0.0197
   0.0202
  -0.0092
  -0.0374
   0.0148
  -0.0335
   0.0040
  -0.0572
   0.0040
  -0.0572
   0.0148
  -0.0335
  -0.0092
  -0.0374
   0.0197
   0.0202
  -0.0197
   0.0156
   0.0200
   0.0761
  -0.0242
   0.0747

j3eig =
  1.2133e-07

j3eigvx =
   0.0206
  -0.0518
  -0.0370
  -0.0552
   0.0097
   0.0333
  -0.0347
   0.0284
  -0.0031
   0.0552
  -0.0190
   0.0633
   0.0002
  -0.0083
  -0.0002
   0.0083
   0.0190
  -0.0633
   0.0031
  -0.0552
   0.0347
  -0.0284
  -0.0097
  -0.0333
   0.0370
   0.0552
  -0.0206
   0.0518

j3eigvy =
   0.0616
  -0.0146
   0.0727
  -0.0164
   0.0453
   0.0010
   0.0647
  -0.0047
   0.0125
   0.0180
   0.0453
   0.0165
  -0.0204
  -0.0017
   0.0204
   0.0017
  -0.0453
  -0.0165
  -0.0125
  -0.0180
  -0.0647
   0.0047
  -0.0453
  -0.0010
  -0.0727
   0.0164
  -0.0616
   0.0146

Plotting the three lowest mode shapes

 for j=1:3
     figure
     plot(eigvect(:,j));
     title(['Mode Shape ',num2str(j)])
 end

Problem R5.5a: Eigen vector plot for zero evals of the 2 bar truss system p.21-2 (fead.f08.mtgs.[21])

On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.

Given: Two member zero evals

Consider a 2 member system. Plot the eigen vectors corresponding to zero evals and interpret the results.

Use standard node and element naming conventions.

Figure 1: Two member system (fig.JPG)

Solution: Plot the eigen values and interpret

This is the general stiffness matrix for a two bar system as given.

${\vec {K}}={\begin{bmatrix}&1&2&3&4&5&6\\1&(l^{(1)})^{2}*K^{(1)}&l^{(1)}m^{(1)}*K^{(1)}&-(l^{(1)})^{2}*K^{(1)}&-l^{(1)}m^{(1)}*K^{(1)}&0&0\\2&l^{(1)}m^{(1)}*K^{(1)}&(m^{(1)})^{2}*K^{(1)}&-l^{(1)}m^{(1)}*K^{(1)}&-(m^{(1)})^{2}*K^{(1)}&0&0\\3&-(l^{(1)})^{2}*K^{(1)}&-l^{(1)}m^{(1)}*K^{(1)}&(l^{(1)})^{2}*K^{(1)}+(l^{(2)})^{2}*K^{(2)}&l^{(1)}m^{(1)}*K^{(1)}+l^{(2)}m^{(2)}*K^{(2)}&-(l^{(2)})^{2}*K^{(2)}&-l^{(2)}m^{(2)}*K^{(2)}\\4&-l^{(1)}m^{(1)}*K^{(1)}&-(m^{(1)})^{2}*K^{(1)}&l^{(1)}m^{(1)}*K^{(1)}+l^{(2)}m^{(2)}*K^{(2)}&(m^{(1)})^{2}*K^{(1)}+(m^{(2)})^{2}*K^{(2)}&-(l^{(2)})^{2}*K^{(2)}&-l^{(2)}m^{(2)}*K^{(2)}\\5&0&0&-(l^{(2)})^{2}*K^{(2)}&-l^{(2)}m^{(2)}*K^{(2)}&(l^{(2)})^{2}*K^{(2)}&l^{(2)}m^{(2)}*K^{(2)}\\6&0&0&-l^{(2)}m^{(2)}*K^{(2)}&-(m^{(2)})^{2}*K^{(2)}&l^{(2)}m^{(2)}*K^{(2)}&(m^{(2)})^{2}*K^{(2)}\\\end{bmatrix}}$

The global stiffness matrix in numerical form match to this specific problem is as follows.

${\vec {K}}={\begin{bmatrix}0.5625&0.3248&-0.5625&-0.3248&0&0\\0.3248&0.1875&-0.3248&-0.1875&0&0\\-0.5625&-0.3248&3.0625&-2.1752&-2.5000&2.5000\\-0.3248&-0.1875&-2.1752&2.6875&2.5000&-2.5000\\0&0&-2.5000&2.5000&2.5000&-2.5000\\0&0&2.5000&-2.5000&-2.5000&2.5000\\\end{bmatrix}}$

The eigen vector matrix is as follows.

${\vec {V}}={\begin{bmatrix}-0.1118&0.5043&-0.0000&-0.5931&0.6174&-0.0139\\-0.0814&-0.8634&0.0000&-0.3476&0.3565&-0.0080\\-0.4628&0.0089&0.0000&-0.4803&-0.5409&0.5123\\0.5266&-0.0053&-0.0000&-0.5429&-0.4330&-0.4904\\-0.4947&0.0071&-0.7071&0.0313&-0.0765&-0.4984\\0.4947&-0.0071&-0.7071&-0.0313&0.0765&0.4984\\\end{bmatrix}}$

${\vec {D}}={\begin{bmatrix}0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&1.4705&0\\0&0&0&0&0&10.0295\\\end{bmatrix}}$

The eigen vectors correspond to the columns of the eigen vector matrix shown above. The eigen value mode shapes are a linear combination of the pure mode shapes (pure rigid body and pure mechanism).

Figure 1: The Vectors plotted from the eigen vector matrix ([1])

function R5_5e2

K= [9/16 (3*sqrt(3))/16 -9/16 -(3*sqrt(3))/16 0 0; 
(3*sqrt(3))/16 3/16 -(3*sqrt(3))/16 -3/16 0 0; 
-9/16 -(3*sqrt(3))/16 49/16 ((3*sqrt(3)-40)/16) -5/2 5/2;
-(3*sqrt(3))/16 -3/16 ((3*sqrt(3)-40)/16) 43/16 5/2 -5/2; 
0 0 -5/2 5/2 5/2 -5/2; 
0 0 5/2 -5/2 -5/2 5/2]

Eval=eig(K)

[V,D]=eig(K)

V
D=abs(D)

%Each column of V is a mode

 for i=1:4
   figure
   plot(V(:,i));
   title(['Mode ',num2str(i)])
 end

end

As a thought experiment, we plotted the position plus the deformation derived from the eigen vector matrix. This will supply 4 shapes but they are not constrained to the boundary conditions. Applying the boundary conditions to the K matrix reduces the number of non zero eigen vector outputs to two. The results are shown below. The figure plots came from the eigen vectors in the fifth and sixth columns of the constrained eigen vector matrix. Using the other columns produced a figure that was not constrained to the fixed supports.

Figure 1: Mode shape constrained to the boundary conditions. The dotted line represents the original shape. ([2])

Figure 1: Mode shape constrained to the boundary conditions. The dotted line represents the original shape. ([3])

function R5_5e

K= [9/16 (3*sqrt(3))/16 -9/16 -(3*sqrt(3))/16 0 0; 
(3*sqrt(3))/16 3/16 -(3*sqrt(3))/16 -3/16 0 0; 
-9/16 -(3*sqrt(3))/16 49/16 ((3*sqrt(3)-40)/16) -5/2 5/2;
-(3*sqrt(3))/16 -3/16 ((3*sqrt(3)-40)/16) 43/16 5/2 -5/2; 
0 0 -5/2 5/2 5/2 -5/2; 
0 0 5/2 -5/2 -5/2 5/2]

%K_red=K([3 4],[3 4]);

K1=[0 0 0 0 0 0;
    0 0 0 0 0 0;
    0 0 K(3,3) K(3,4) 0 0;
    0 0 K(4,3) K(4,4) 0 0;
    0 0 0 0 0 0;
    0 0 0 0 0 0]

[V D] = eig(K1)

N=[1 2;
    2 3];

P=[0 cos(pi/6)*4 cos(pi/6)*4+cos(pi/4)*2;
   0 sin(pi/6)*4 sin(pi/6)*4-sin(pi/4)*2];

for i=1:2:5
    x_1((i+1)/2)=P(1,((i+1)/2))+V(i,1);
end

for i=2:2:6
    y_1((i/2))=P(2,(i/2))+V(i,1);
end
 
%Plot deformed system with constraints
hold on
for i=1:2
    l1=N(1,i);
    l2=N(2,i);
    x1=[x_1(l1),x_1(l2)];
    y1=[y_1(l1),y_1(l2)];
    axis([-1 5 -1 5])
    plot(x1,y1,'b')
    title(['Constrained Shape'])
    hold on
end

%Plot undeformed system
for i=1:2:5
    x_o((i+1)/2)=P(1,((i+1)/2));
end

for i=2:2:6
    y_o((i/2))=P(2,(i/2));
end
 for i=1:2
    l1=N(1,i);
    l2=N(2,i);
    x1=[x_o(l1),x_o(l2)];
    y1=[y_o(l1),y_o(l2)];
    axis([-1 5 -1 5])
    plot(x1,y1,'-.or')
    hold on
 end
end

Problem R5.5b: Eigen vector plot for zero evals of the square 3 bar truss system p.21-3 (figure a) (fead.f08.mtgs.[21])

On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.

Given: Square 3 bar truss system

Consider a 3 member system. Plot the eigen vectors corresponding to zero evals and interpret the results.

a=b=1 E=2 A=3

Figure 1: Two member system (b.JPG)

Find:

1.Plot the eigen values

Use standard node and element naming conventions.

Solution: Plot the eigen values

${\vec {V}}={\begin{bmatrix}-0.7071&0&0&-0.7071\\0&1.0000&0&0\\-0.7071&0&0&0.7071\\0&0&1.0000&0\\\end{bmatrix}}$

${\vec {D}}={\begin{bmatrix}0&0&0&0\\0&6&0&0\\0&0&6&0\\0&0&0&12\\\end{bmatrix}}$

Figure 1: The only shape corresponding to zero evals. ([4])

function R5_5ec
E=2;
A=3;
L=1;
k=(E*A)/L;
k1=k*[0 0 0 0;
    0 1 0 -1;
    0 0 0 0;
    0 -1 0 1]
k3=k*[0 0 0 0;
    0 1 0 -1;
    0 0 0 0;
    0 -1 0 1]
k2=k*[1 0 -1 0;
    0 0 0 0;
    -1 0 1 0;
    0 0 0 0]

K=zeros(8,8)

K(1:4,1:4)=k1
K(5:8,5:8)=k3

Kt=zeros(8,8)
Kt(3:6,3:6)=k2

Kg=K+Kt

%boundary conditions applied
K1=[0 0 0 0 0 0 0 0;
    0 0 0 0 0 0 0 0;
    0 0 Kg(3,3) Kg(3,4) Kg(3,5) Kg(3,6) 0 0;
    0 0 Kg(4,3) Kg(4,4) Kg(4,5) Kg(4,6) 0 0;
    0 0 Kg(5,3) Kg(5,4) Kg(5,5) Kg(5,6) 0 0;
    0 0 Kg(6,3) Kg(6,4) Kg(6,5) Kg(6,6) 0 0;
    0 0 0 0 0 0 0 0;
    0 0 0 0 0 0 0 0]

Kred=[Kg(3,3) Kg(3,4) Kg(3,5) Kg(3,6);
     Kg(4,3) Kg(4,4) Kg(4,5) Kg(4,6);
     Kg(5,3) Kg(5,4) Kg(5,5) Kg(5,6);
     Kg(6,3) Kg(6,4) Kg(6,5) Kg(6,6)]

[V D] = eig(Kred)

 for i=1:6
   figure
   plot(V(:,i));
   title(['Mode ',num2str(i)])
 end

end

Problem R5.6

On my honor, I have neither given nor recieved unauthorized aid in doing this assignment.

Description

We are to solve Pb-53.6 p.53-13b over again using the modal superposition method.

Given:

We are given from Pb-53.6 that:

$m_{1}=3$, $m_{2}=2$

$k_{1}=10$, $k_{2}=20$, $k_{3}=15$

$c_{1}=1/2$, $c_{2}=1/4$, $c_{3}=1/3$

$F_{1}(t)=0$, $F_{2}(t)=0$

We also know from Pb-53.9 that:

$\lambda _{1}=4.765$

$\lambda _{2}=22.735$

$\phi _{1}={\begin{bmatrix}1.273\\1\\\end{bmatrix}}$

$\phi _{2}={\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}$

$M={\begin{bmatrix}m_{1}&0\\0&m_{2}\\\end{bmatrix}}$ and $K={\begin{bmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{2}+k_{3}\\\end{bmatrix}}$ and $C={\begin{bmatrix}c_{1}+c_{2}&-c_{2}\\-c_{2}&c_{2}+c_{3}\\\end{bmatrix}}$

Therefore, we have:

$M={\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}$ and $K={\begin{bmatrix}30&-20\\-20&35\\\end{bmatrix}}$ and $C={\begin{bmatrix}3/4&-1/4\\-1/4&7/12\\\end{bmatrix}}$

Solution:

From Pb-53.9, we already know the eigenvectors. To solve the problem using superposition, we know only need to find the modal coordinates of d(t) corresponding to the mode shapes. That is to say, we need to find z so as to solve the equation:

$d(t)=z_{1}\phi _{1}+z_{2}\phi _{2}$

We can get this from:

$z_{j}^{''}+{\bar {\phi }}_{i}^{T}C{\bar {\phi }}_{j}z_{j}^{'}+(w_{j})^{2}z_{j}={\bar {\phi }}_{j}^{T}F(t)$

Since F(t) = 0, the above differential equation becomes homogeneous. However, we still need to find ${\bar {\phi }}_{1}$ and ${\bar {\phi }}_{2}$. These can be found from the equation:

${\bar {\phi }}_{i}={\frac {\phi _{i}}{\sqrt {\phi _{i}^{T}M\phi _{i}}}}$, therefore,

${\bar {\phi }}_{1}={\frac {\begin{bmatrix}1.273\\1\\\end{bmatrix}}{\sqrt {{\begin{bmatrix}1.273&1\\\end{bmatrix}}{\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}{\begin{bmatrix}1.273\\1\\\end{bmatrix}}}}}={\frac {\begin{bmatrix}1.273\\1\\\end{bmatrix}}{\sqrt {6.86}}}={\frac {\begin{bmatrix}1.273\\1\\\end{bmatrix}}{2.619}}={\begin{bmatrix}0.485\\0.381\\\end{bmatrix}}$

${\bar {\phi }}_{2}={\frac {\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}{\sqrt {{\begin{bmatrix}-0.5234&1\\\end{bmatrix}}{\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}{\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}}}}={\frac {\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}{\sqrt {2.82}}}={\frac {\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}{1.68}}={\begin{bmatrix}-0.311\\0.595\\\end{bmatrix}}$

Remembering that $(w_{j})^{2}=\lambda _{j}$, our first differential equation becomes:

$z_{1}^{''}+{\begin{bmatrix}0.485&0.381\\\end{bmatrix}}{\begin{bmatrix}3/4&-1/4\\-1/4&7/12\\\end{bmatrix}}{\begin{bmatrix}0.485\\0.381\\\end{bmatrix}}z_{1}^{'}+4.765z_{1}=0$

$z_{1}^{''}+0.1687z_{1}^{'}+4.765z_{1}=0$

Using the method of undetermined coefficients for solving differential equations, we arrive at:

$z_{1}=Ae^{-0.0843t}cos(2.18t)$

We now need to find the modal coordinate initial condition using the following equaiton:

$z_{i}(0)={\bar {\phi }}_{i}^{T}Md(0)$

$z_{1}(0)={\begin{bmatrix}0.485&0.381\\\end{bmatrix}}{\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}{\begin{bmatrix}-1\\2\\\end{bmatrix}}=0.069$

We can easily find A from:

$z_{1}(0)=A(1)(1)=0.069$

so

$z_{1}=0.069e^{-0.0843t}cos(2.18t)$

Our second differential equation is:

$z_{2}^{''}+{\begin{bmatrix}-0.311&0.595\\\end{bmatrix}}{\begin{bmatrix}3/4&-1/4\\-1/4&7/12\\\end{bmatrix}}{\begin{bmatrix}-0.311\\0.595\\\end{bmatrix}}z_{2}^{'}+22.735z_{2}=0$

$z_{2}^{''}+0.371z_{2}^{'}+22.735z_{2}=0$

Using the method of undetermined coefficients for solving differential equations once again, we obtain:

$z_{2}=Be^{-0.185t}cos(4.76t)$

We now need to find the modal coordinate initial condition using the following equaiton:

$z_{i}(0)={\bar {\phi }}_{i}^{T}Md(0)$

$z_{2}(0)={\begin{bmatrix}-0.311&0.595\\\end{bmatrix}}{\begin{bmatrix}3&0\\0&2\\\end{bmatrix}}{\begin{bmatrix}-1\\2\\\end{bmatrix}}=3.313$

We can easily find B from:

$z_{2}(0)=B(1)(1)=3.313$

so

$z_{2}=3.313e^{-0.0843t}cos(2.18t)$

The solution using modal superposition can then be displayed as:

$d(t)=0.069e^{-0.0843t}cos(2.18t){\begin{bmatrix}1.273\\1\\\end{bmatrix}}+3.313e^{-0.185t}cos(4.76t){\begin{bmatrix}-0.5234\\1\\\end{bmatrix}}$

Problem R5.7: Consider the free vibration of truss system p.53-22b (fead.f13.sec53b.[21])

On our honor, we did this assignment on our own.

Given: Truss system under free vibration with applied force and zero initial velocity

Consider the truss system. The initial force is applied at node four and the force equals five.

Use standard node and element naming conventions.

Figure 1: Truss system (fead.f13.sec53b p.53-22b). ([5])

Solution: Solve for the truss motion

K =

 Columns 1 through 5

   3.3839    0.8839   -2.5000         0   -0.8839
   0.8839    0.8839         0         0   -0.8839
  -2.5000         0    5.8839    0.8839         0
        0         0    0.8839    3.3839         0
  -0.8839   -0.8839         0         0    4.2678
  -0.8839   -0.8839         0   -2.5000         0
        0         0   -2.5000         0   -0.8839
        0         0         0         0    0.8839
        0         0   -0.8839   -0.8839   -2.5000
        0         0   -0.8839   -0.8839         0
        0         0         0         0         0
        0         0         0         0         0

 Columns 6 through 10

  -0.8839         0         0         0         0
  -0.8839         0         0         0         0
        0   -2.5000         0   -0.8839   -0.8839
  -2.5000         0         0   -0.8839   -0.8839
        0   -0.8839    0.8839   -2.5000         0
   4.2678    0.8839   -0.8839         0         0
   0.8839    5.8839   -0.8839         0         0
  -0.8839   -0.8839    3.3839         0   -2.5000
        0         0         0    4.2678         0
        0         0   -2.5000         0    4.2678
        0   -2.5000         0   -0.8839    0.8839
        0         0         0    0.8839   -0.8839

 Columns 11 through 12

        0         0
        0         0
        0         0
        0         0
        0         0
        0         0
  -2.5000         0
        0         0
  -0.8839    0.8839
   0.8839   -0.8839
   3.3839   -0.8839
  -0.8839    0.8839

p = 2;
E = 5;
A = 0.5;
L = 1;
Ld = 1*sqrt(2);

%degree of freedom for each element
dof = zeros(10,5);
dof(1,:) = [1 1 2 3 4];
dof(2,:) = [2 1 2 5 6];
dof(3,:) = [3 3 4 5 6];
dof(4,:) = [4 5 6 9 10];
dof(5,:) = [5 5 6 7 8];
dof(6,:) = [6 3 4 9 10];
dof(7,:) = [7 3 4 7 8];
dof(8,:) = [8 7 8 9 10];
dof(9,:) = [9 9 10 11 12];
dof(10,:) = [10 7 8 11 12];

%position of each node
pos = zeros(2,6);
pos(:,1) = [0;0];
pos(:,2) = [L;0];
pos(:,3) = [L;L];
pos(:,4) = [2*L;0];
pos(:,5) = [2*L;L];
pos(:,6) = [3*L;0];

%Connections
conn = zeros(2,10);
conn(:,1) = [1;2];
conn(:,2) = [1;3];
conn(:,3) = [2;3];
conn(:,4) = [3;5];
conn(:,5) = [3;4];
conn(:,6) = [2;5];
conn(:,7) = [2;4];
conn(:,8) = [4;5];
conn(:,9) = [5;6];
conn(:,10) = [4;6];

%seperates into x and y coordinates
x = zeros(10,2);
y = zeros(10,2);
for i = 1:10
    x(i,:) = [pos(1,conn(1,i)),pos(1,conn(2,i))];
    y(i,:) = [pos(2,conn(1,i)),pos(2,conn(2,i))];
end

%Set up K and M matrix
K = zeros(12);
M = zeros(12);
for i = 1:10
    xm = x(i,2)-x(i,1);
    ym = y(i,2)-y(i,1);
    L = sqrt(xm^2+ym^2);
    l = xm/L;
    m = ym/L;
    k = E*A/L*[l^2 l*m -l^2 -l*m;l*m m^2 -l*m -m^2;-l^2 -l*m l^2 l*m;-l*m -m^2 l*m m^2;];
    m = L*A*p;
    m = [m/2 0 0 0;0 m/2 0 0;0 0 m/2 0;0 0 0 m/2];
    Dof = dof(i,2:5);
    K(Dof,Dof) = K(Dof,Dof)+k;
    M(Dof,Dof) = M(Dof,Dof)+m;
end

Table of Assignments R5

Problem Assignments R5
Problem #	Solved&Typed by	Reviewed by
1	David Bonner, Vernon Babich	All
2	Chad Colocar, David Bonner	All
3	Bryan Tobin, Tyler Wulterkens	All
4	Tyler Wulterkens, Vernon Babich	All
5	Vernon Babich, Tyler Wulterkens	All
6	David Bonner, Vernon Babich	All
7	Tyler Wulterkens, Chad Colocar, Vernon Babich	All