University of Florida/Eml4507/Team 7 Report 1

Problem R1.1: MATLAB Primer

Given

The MATLAB Primer document. It can be viewed here: MATLAB Primer document.

Find

Reproduce all of the examples in the MATLAB Primer document.

Solution

2. Entering Matrices.

There are many different ways that a matrix can be entered into MATLAB.

Both of the following ways can be used to create a matrix in MATLAB, and as can be seen, they both produce the same result.

>> A=[1 2 3; 4 5 6; 7 8 9]

A =

    1     2     3

    4     5     6

    7     8     9

>> A=[

1 2 3

4 5 6

7 8 9

]

A =

    1     2     3

    4     5     6

    7     8     9

There are also different ways to input a matrix involving complex numbers into MATLAB.

Here are two different ways that produce the same result in MATLAB.

A =

  1.0000 + 5.0000i   2.0000 + 6.0000i

  3.0000 + 7.0000i   4.0000 + 8.0000i

>> A=[1+5i 2+6i;3+7i 4+8i]

A =

  1.0000 + 5.0000i   2.0000 + 6.0000i

  3.0000 + 7.0000i   4.0000 + 8.0000i

3. Matrix operations, array operations.

When doing matrix operations, the operation needs to be proceeded by a dot, whereas your usual operations do not. Different operations can be used to obtain a result. For example,

>> [1,2,3,4].*[1,2,3,4]

ans =

    1     4     9    16

produces the same result as

>> [1,2,3,4].^2

ans =

    1     4     9    16

5. Matrix building functions.

The code zeros(m,n) creates a matrix of size m by n of zeroes, and the code zeros(n) creates a matrix of size n by n. If there is a matrix called A, then the code zeros(size(A)) will produce a matrix that is the same size as A. If there is a vector called x, then the code diag(x) will create a matrix where x is the diagonal of the matrix. For example, if

>> A=[1 2; 3 4]

A =

    1     2

    3     4

then

>> diag(diag(A))

ans =

1 0

4 0

Matrices can also be built from blocks. For example, if

>> A=[1 2 3; 4 5 6; 7 8 9]

A =

    1     2     3

    4     5     6

    7     8     9

then

>> B=[A, zeros(3,2); zeros(2,3), eye(2)]

B =

    1     2     3     0     0

    4     5     6     0     0

    7     8     9     0     0

    0     0     0     1     0

    0     0     0     0     1

Thus creating a 5 by 5 matrix called B.

6. For, while, if – and relations.

MATLAB can act like most other computer programs when doing flow control statements.

When using the for statement, the code needs to be in the form of the following, however, notice how the two following statements are written to be the reverse of the other.

>> n=5;

>> x=[]; for i=1:n, x=[x,i^2], end

x =

    1

x =

    1     4

x =

    1     4     9

x =

    1     4     9    16

x =

    1     4     9    16    25

>> x=[]; for i=n:-1:1, x=[x,i^2], end

x =

   25

x =

   25    16

x =

   25    16     9

x =

   25    16     9     4

x =

   25    16     9     4     1

A for statement can also be used to create a m by n Hilbert matrix.

If n=5 and m=5, then

>> for i=1:m; for j=1:n; H(i,j)=1/(i+j-1); end;end;H

H =

   1.0000    0.5000    0.3333    0.2500    0.2000

   0.5000    0.3333    0.2500    0.2000    0.1667

   0.3333    0.2500    0.2000    0.1667    0.1429

   0.2500    0.2000    0.1667    0.1429    0.1250

   0.2000    0.1667    0.1429    0.1250    0.1111

The for statement also allows a matrix to be used instead of using the code 1:n. For example, the following can compute the sum of all the elements in A by adding its column sums.

If

A =

    1     2     3

    4     5     6

    7     8     9

Then

>> s=0; for c=A; s=s+sum(c); end

>> s

s =

   45

Another loop that can be used is the while loop. A while loop keeps computing the loops statements until the while relation becomes untrue. For example, the following will loop until it discovers the smallest integer n that satisfies the statement 2n ≥ a.

If a=5, then

>> n=0; while 2^n < a; n=n+1; end; n

n =

    3

An if statement is similar to a while loop in the way that it will keep computing until the if statement’s relation becomes untrue. The following is an example of a typical if statement.

If n = -2, then

>> if n<0

parity=0

elseif rem(n,2)==0

parity=2

else

parity=1

end

parity =

    0

8. Vector functions.

There are many useful vector functions that can be used in MATLAB, such as max, min, sort, sum, prod, median, mean, std, any, and all. For example, if

A =

    1     2     3

    4     5     6

    7     8     9

then the maximum element in matrix A can be found by

>> max(max(A))

ans =

    9

9. Matrix functions.

MATLAB has many preset functions that can be used, and many of them can produce multiple outputs. For example, to find the Eigen values of the matrix A, the following code can be used.

If

A =

    1     2     3

    4     5     6

    7     8     9

then

>> y=eig(A)

y =

  16.1168

  -1.1168

  -0.0000

Two matrices can also be created called U and D, where U is a matrix whose columns are the eigenvectors of A, and where D is a diagonal matrix that has its diagonal consist of the eigenvalues of matrix A.

>> [U,D]=eig(A)

U =

  -0.2320   -0.7858    0.4082

  -0.5253   -0.0868   -0.8165

  -0.8187    0.6123    0.4082

D =

  16.1168         0         0

        0   -1.1168         0

        0         0   -0.0000

10. Command line editing and recall.

Using MATLAB, it is also useful to compares functions and graphs at times, and to repeatedly recall functions to tweak and change small values in. For example, the following code is useful if one wanted to compare the graphs of y=sin(nx) and y=sin(mx). Then these functions could be recalled and repeated comparisons could be done if m and n values were changed and experimented with.

>> m=2;

>> n=3;

>> x=0:.01:2*pi;

>> y=sin(m*x);

>> z=cos(n*x);

>> plot(x,y,x,z)

11. Submatrices and colon notation.
Submatrices and colon notation are both very useful operations in MATLAB because they both reduce the need for loops, which is important because loops can slow down MATLAB if large files of data are being used. Colon notation is a useful way for representing matrices. For example, the code 1:5 actually represents a vector as can be seen below.

>> 1:5

ans =

    1     2     3     4     5

By default, MATLAB will make the spacing between elements of a vector equal to one. However, the increment between elements can be changed. For example,

>> 0.2:0.2:1.2

ans =

   0.2000    0.4000    0.6000    0.8000    1.0000    1.2000

>> 5:-1:1

ans =

    5     4     3     2     1

This way of coding can then be expanded into creating tables. For example, to create a table of sines can be shown below.

>> x=[0:.1:2]';
>> y=sin(x);
>> [x y]

ans =

        0         0

   0.1000    0.0998

   0.2000    0.1987

   0.3000    0.2955

   0.4000    0.3894

   0.5000    0.4794

   0.6000    0.5646

   0.7000    0.6442

   0.8000    0.7174

   0.9000    0.7833

   1.0000    0.8415

   1.1000    0.8912

   1.2000    0.9320

   1.3000    0.9636

   1.4000    0.9854

   1.5000    0.9975

   1.6000    0.9996

   1.7000    0.9917

   1.8000    0.9738

   1.9000    0.9463

   2.0000    0.9093

Colon notation is also very useful in accessing the submatrices of a matrix. For example, if there was a matrix A.

>> A=[1:5;1:5;1:5;1:5;1:5]

A =

    1     2     3     4     5

    1     2     3     4     5

    1     2     3     4     5

    1     2     3     4     5

    1     2     3     4     5

Then, for example, you could access the first four entries of the third column.
>> A(1:4,3)

ans =

    3

    3

    3

    3

A colon all by itself represents an entire row or column. For example,
>> A(:,3)

ans =

    3

    3

    3

    3

    3

>> A(1:4,:)

ans =

    1     2     3     4     5

    1     2     3     4     5

    1     2     3     4     5

    1     2     3     4     5

Furthermore, arbitrary integral vectors can be used as subscripts. For example,

>> A(:,[2 4])

ans =

    2     4

    2     4

    2     4

    2     4

0 4

Subscripts like these can be used on both sides of an assignment. For example, if there was a matrix B, then the following code could replace the columns 2,4,5 of A with the first three columns of B.

>> B=A'

B =

    1     1     1     1     1

    2     2     2     2     2

    3     3     3     3     3

    4     4     4     4     4

    5     5     5     5     5

>> A(:,[2 4 5])=B(:,1:3)

A =

    1     1     3     1     1

    1     2     3     2     2

    1     3     3     3     3

    1     4     3     4     4

    1     5     3     5     5

Parts of a matrix can also be multiplied by other matrices. For example, the columns 2 and 4 of A can be multiplied by a matrix.

>> A(:,[2,4])=A(:,[2,4])*[1 2;3 4]

A =

    1     4     3     6     1

    1     8     3    12     2

    1    12     3    18     3

    1    16     3    24     4

    1    20     3    30     5

Furthermore, the order of elements in a matrix can be flipped and a horizontal matrix can be flipped into a vertical matrix and vice versa. This can be done by using a number of different commands, like the following.

>> n=5;
>> x=[1 2 3 4 5]

x =

    1     2     3     4     5

>> x=x(n:-1:1)

x =

    5     4     3     2     1

>> y=fliplr(x)

y =

    1     2     3     4     5

>> y=flipud(x')

y =

    1

    2

    3

    4

    5

Section 12 M-files

Random integer matrix generator function a =randint(m,n,a,b)

if nargin <3, a=0; b=9; end a=floor((b-a+1)*rand(m,n))+a;

EDU>> randint(4,5)

ans =

    8     6     9     9     4
    9     0     9     4     9
    1     2     1     8     7
    9     5     9     1     9

Shows multiple outputs for a function function [mean,stdev]=stat(x)

[m n] = size(x) if m==1

   m=n;

end mean =sum(x)/m; stdev=sqrt(sum(x.^2)/m-mean.^2);

EDU>> stat(4)

m = 1 n = 1 ans = 4

Storing E into memory EDU>> M=magic(6); E=zeros(6,50); for j=1:50 E(:,j)=eig(M^i); end

This code returns a zero of a function of one variable via the bisection method function [b,steps]=bisectFEA(fun,x,tol)

if nargin <3, tol-eps;end trace=(nargout==2); if x~=0, dx =x/20;else, dx=1/20;end a=x-dx; fa=feval(fun,a); b=x+dx; fb=feval(fun,b);

while (fa>0)==(fb>0)

   dx=2.0*dx;
   a=x-dx; fa=feval(fun,a)
   if (fa>0) ~= (fb>0), break, end
   b=x+dx; fb=feval(fun,b);

end if trace, steps=[a fa; b fb]; end

while abs(b-a) >2.0*tol*max(abs(b),1.0)

   c= a+0.5*(b-a); fc=feval(fun,c);
   if trace, steps=[steps; [c fc]]; end
   if (fb>0)==(fc>0)
       b=c; fb=fc;
   else
       a=c; fa=fc;
   end

end

Section 13 text strings, error messages, input

EDU>> s='this is a test'

s =

this is a test

EDU>> disp('this message is hereby displayed') error('sorry, the matrix must be symmetric') this message is hereby displayed ??? sorry, the matrix must be symmetric

EDU>> iter=input('enter the number of iterations: ') enter the number of iterations: 3

iter =

    3

Section 14: Managing M-files

EDU>> !ed rotate.m 'ed' is not recognized as an internal or external command, operable program or batch file.

Section 15: Comparing efficiency of algorithms: flops, tic and toc

Tic and toc before and after a statement gives EDU>> tic, any statement, toc

ans =

    1

Elapsed time is 0.000838 seconds.

Section 16: Output format

No example

Section 17 Hardcopy

EDU>> diary brandon EDU>> ksfh;hr;ghwlrih;gwoi;r ??? Undefined function or variable 'ksfh'.

EDU>> yo ??? Undefined function or variable 'yo'.

EDU>> y=12;x=45; EDU>> diary off

Below is what appeared in the file named “Brandon”

uiopen('C:\Users\Brandon\Documents\MATLAB\brandon',1) ksfh;hr;ghwlrih;gwoi;r {_??? Undefined function or variable 'ksfh'. }_ yo {_??? Undefined function or variable 'yo'. }_ uiopen('C:\Users\Brandon\Documents\MATLAB\brandon',1) y=12;x=45; uiopen('C:\Users\Brandon\Documents\MATLAB\brandon',1) diary off

Section 18. Graphics

Planar plots

EDU>> x=-1.5:.01:1.5; y=exp(-x.^2); plot(x,y)

Section 18 figure 1

3-D line plots EDU>> t=.01:.01:20*pi; x=cos(t); y=sin(t); z=t.^3; plot3(x,y,z)

3-D mesh and surface plots

EDU>> [x,y]=meshgrid(-1:.2:2, -2:.2:2); z=exp(-x.^2-y.^2); mesh(z)

Section 18 figure 3

function [x,y,z]=torus(r,n,a)

if nargin <3, a=1; end if nargin <2, n=30; end if nargin <1, r=0.5; end theta=pi*(0:2:2*n)/n; phi=2*pi*(0:2:n)'/n; xx=(a+r*cos(phi))*cos(theta); yy=(a+r*cos(phi))*sin(theta); zz=r*sin(phi)*ones(size(theta)); if nargout == 0

   surf(xx,yy,zz)
   ar=(a+r)/sqrt(2);
   axis([-ar,ar,-ar,ar,-ar,ar])

else

   x=xx; y=yy ; z=zz;

end

Section 19: Sparse Matrix Computations

EDU>> F=floor(10*rand(6)); F=triu(tril(F,1),-1); EDU>> S=sparse(F)

S =

  (1,1)        8
  (2,1)        9
  (1,2)        2
  (2,2)        5
  (3,2)        9
  (2,3)        4
  (3,3)        8
  (4,3)        1
  (3,4)        6
  (5,4)        8
  (4,5)        3
  (5,5)        6
  (6,5)        1
  (6,6)        8

EDU>> F=full(S)

F =

    8     2     0     0     0     0
    9     5     4     0     0     0
    0     9     8     6     0     0
    0     0     1     0     3     0
    0     0     0     8     6     0
    0     0     0     0     1     8

EDU>> issparse(A) ??? Undefined function or variable 'A'.

EDU>> m=6; n=6; e=ones(n,1); d=-2*e; EDU>> T=spdiags([e,d,e],[-10,1],m,n)

T =

  (1,2)       -2
  (2,3)       -2
  (3,4)       -2
  (4,5)       -2
  (5,6)       -2

EDU>> i=[1 2 3 4 4 4]; j=[1 2 3 1 2 3]; s=[5 6 7 8 9 10]; EDU>> S=sparse(i,j,s,4,3), full(S)

S =

  (1,1)        5
  (4,1)        8
  (2,2)        6
  (4,2)        9
  (3,3)        7
  (4,3)       10

ans =

    5     0     0
    0     6     0
    0     0     7
    8     9    10

EDU>> n=6;e=floor(10*rand(n-1,1)); E=sparse(2:n,1:n-1,e,n,n)

E =

  (2,1)        6
  (3,2)        3
  (4,3)        9
  (6,5)        4

On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.

Problem R1.2: Equation of Motion Derivation

Given

Two Spring-Mass-Damper Systems

Figure A.

Figure B.

Find

Derive the differential equation of motion for each of the systems.

Solution

Part A

For Figure A, we see that the system is fixed on both ends with an applied force $f(t)$. The Free Body Diagram of the mass is as follows:

Note that for the forces, we have:

$\displaystyle f_{c}=cy'$

and

$\displaystyle f_{k}=ky$

Applying Newton's second law to the system:

$\displaystyle \sum F=f(t)-f_{k}-f_{c}=ma$

By definition, the acceleration can be as follows:

$\displaystyle a=y''$

Substituting the known values, we can now obtain the equation of motion:

$\displaystyle my''+cy'+ky=f(t)$

Part B

For Figure B, the system is only fixed on one end with an applied force, $f(t)$. Therefore the free body diagram is as follows:

Since the spring and damper forces are along the same line and due to Newton's Third Law, we can make this definition:

$\displaystyle f_{T}=f_{k}=f_{c}$

If Newtons Second Law is applied to the system the same way as in Figure A:

$\displaystyle \sum F=ma$

$\displaystyle \sum F=f(t)-f_{T}=ma$

Acceleration can be defined as:

$\displaystyle a=y''$

Where the equation of motion now becomes:

$\displaystyle f(t)-f_{T}=ma=my''$

Rearranging, the Equation of motion is:

$\displaystyle my''+f_{T}=f(t)$

On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.

Problem R1.3: Element Stiffness Matrix

Given

Figure 1: Truss with two elastic bars

Element length: L⁽¹⁾=4, L⁽²⁾=2; Young's modulus: E⁽¹⁾=3, E⁽²⁾=5; Cross section area: A⁽¹⁾=1, A⁽²⁾=2;

Find

Provide the numerical values for the elem stiff matrices $\mathbf {k^{(1)}}$ and $\mathbf {k^{(2)}}$; and find the coordinates of the global nodes 1 and 3, with the global node 2 at the origin of the global coord system.

Solution

The director cosines for an element are given by:

$\displaystyle {\begin{aligned}&l^{(e)}=\cos \theta ^{(e)}\\&m^{(e)}=\sin \theta ^{(e)}\end{aligned}}$

For element one θ=30° so the director cosines are

$\displaystyle {\begin{aligned}&l^{(1)}=\cos 30^{\circ }={\frac {\sqrt {3}}{2}}\\&m^{(1)}=\sin 30^{\circ }={\frac {1}{2}}\end{aligned}}$

For element two θ=-45° so the director cosines are

$\displaystyle {\begin{aligned}&l^{(2)}=\cos -45^{\circ }={\frac {\sqrt {2}}{2}}\\&m^{(2)}=\sin -45^{\circ }=-{\frac {\sqrt {2}}{2}}\end{aligned}}$

The stiffness of an element is given by:

$k^{(e)}={\frac {E^{(e)}A^{(e)}}{L^{(e)}}}$

Where E is the element's Young's Modulus, A is the area, and L is the length.

For elements one and two:

$\displaystyle {\begin{aligned}&k^{(1)}={\frac {E^{(1)}A^{(1)}}{L^{(1)}}}={\frac {(3)(1)}{(4)}}={\frac {3}{4}}\\&k^{(2)}={\frac {E^{(2)}A^{(2)}}{L^{(2)}}}={\frac {(5)(2)}{(2)}}=5\end{aligned}}$

The element stiffness matrix is given by:

$\mathbf {k^{(e)}} =k^{(e)}{\begin{bmatrix}(l^{(e)})^{2}&l^{(e)}m^{(e)}&-(l^{(e)})^{2}&-l^{(e)}m^{(e)}\\l^{(e)}m^{(e)}&(m^{(e)})^{2}&-l^{(e)}m^{(e)}&-(m^{(e)})^{2}\\-(l^{(e)})^{2}&-l^{(e)}m^{(e)}&(l^{(e)})^{2}&l^{(e)}m^{(e)}\\-l^{(e)}m^{(e)}&-(m^{(e)})^{2}&l^{(e)}m^{(e)}&(m^{(e)})^{2}\end{bmatrix}}$

Element 1

$\displaystyle {\begin{aligned}&\mathbf {k^{(1)}} =k^{(1)}{\begin{bmatrix}(l^{(1)})^{2}&l^{(1)}m^{(1)}&-(l^{(1)})^{2}&-l^{(1)}m^{(1)}\\l^{(1)}m^{(1)}&(m^{(1)})^{2}&-l^{(1)}m^{(1)}&-(m^{(1)})^{2}\\-(l^{(1)})^{2}&-l^{(1)}m^{(1)}&(l^{(1)})^{2}&l^{(1)}m^{(1)}\\-l^{(1)}m^{(1)}&-(m^{(1)})^{2}&l^{(1)}m^{(1)}&(m^{(1)})^{2}\end{bmatrix}}\\&\mathbf {k^{(1)}} =\left({\frac {3}{4}}\right){\begin{bmatrix}\left({\frac {\sqrt {3}}{2}}\right)^{2}&\left({\frac {\sqrt {3}}{2}}\right)\left({\frac {1}{2}}\right)&-\left({\frac {\sqrt {3}}{2}}\right)^{2}&-\left({\frac {\sqrt {3}}{2}}\right)\left({\frac {1}{2}}\right)\\\left({\frac {\sqrt {3}}{2}}\right)\left({\frac {1}{2}}\right)&\left({\frac {1}{2}}\right)^{2}&-\left({\frac {\sqrt {3}}{2}}\right)\left({\frac {1}{2}}\right)&-\left({\frac {1}{2}}\right)^{2}\\-\left({\frac {\sqrt {3}}{2}}\right)^{2}&-\left({\frac {\sqrt {3}}{2}}\right)\left({\frac {1}{2}}\right)&\left({\frac {\sqrt {3}}{2}}\right)^{2}&\left({\frac {\sqrt {3}}{2}}\right)\left({\frac {1}{2}}\right)\\-\left({\frac {\sqrt {3}}{2}}\right)\left({\frac {1}{2}}\right)&-\left({\frac {1}{2}}\right)^{2}&\left({\frac {\sqrt {3}}{2}}\right)\left({\frac {1}{2}}\right)&\left({\frac {1}{2}}\right)^{2}\end{bmatrix}}\\&\mathbf {k^{(1)}} ={\begin{bmatrix}{\frac {9}{16}}&{\frac {3{\sqrt {3}}}{16}}&-{\frac {9}{16}}&-{\frac {3{\sqrt {3}}}{16}}\\{\frac {3{\sqrt {3}}}{16}}&{\frac {3}{16}}&-{\frac {3{\sqrt {3}}}{16}}&-{\frac {3}{16}}\\-{\frac {9}{16}}&-{\frac {3{\sqrt {3}}}{16}}&{\frac {9}{16}}&{\frac {3{\sqrt {3}}}{16}}\\-{\frac {3{\sqrt {3}}}{16}}&-{\frac {3}{16}}&{\frac {3{\sqrt {3}}}{16}}&{\frac {3}{16}}\end{bmatrix}}={\begin{bmatrix}{0.5625}&{0.3248}&{-0.5625}&{-0.3248}\\{0.3248}&{0.1875}&{-0.3248}&{-0.1875}\\{-0.5625}&{-0.3248}&{0.5625}&{0.3248}\\{-0.3248}&{-0.1875}&{0.3248}&{0.1875}\end{bmatrix}}\end{aligned}}$

Element 2

$\displaystyle {\begin{aligned}&\mathbf {k^{(2)}} =k^{(2)}{\begin{bmatrix}(l^{(2)})^{2}&l^{(2)}m^{(2)}&-(l^{(2)})^{2}&-l^{(2)}m^{(2)}\\l^{(2)}m^{(2)}&(m^{(2)})^{2}&-l^{(2)}m^{(2)}&-(m^{(2)})^{2}\\-(l^{(2)})^{2}&-l^{(2)}m^{(2)}&(l^{(2)})^{2}&l^{(2)}m^{(2)}\\-l^{(2)}m^{(2)}&-(m^{(2)})^{2}&l^{(2)}m^{(2)}&(m^{(2)})^{2}\end{bmatrix}}\\&\mathbf {k^{(1)}} =\left(5\right){\begin{bmatrix}\left({\frac {\sqrt {2}}{2}}\right)^{2}&\left({\frac {\sqrt {2}}{2}}\right)\left(-{\frac {\sqrt {2}}{2}}\right)&-\left({\frac {\sqrt {2}}{2}}\right)^{2}&-\left({\frac {\sqrt {2}}{2}}\right)\left(-{\frac {\sqrt {2}}{2}}\right)\\\left({\frac {\sqrt {2}}{2}}\right)\left(-{\frac {\sqrt {2}}{2}}\right)&\left(-{\frac {\sqrt {2}}{2}}\right)^{2}&-\left({\frac {\sqrt {2}}{2}}\right)\left(-{\frac {\sqrt {2}}{2}}\right)&-\left(-{\frac {\sqrt {2}}{2}}\right)^{2}\\-\left({\frac {\sqrt {2}}{2}}\right)^{2}&-\left({\frac {\sqrt {2}}{2}}\right)\left(-{\frac {\sqrt {2}}{2}}\right)&\left({\frac {\sqrt {2}}{2}}\right)^{2}&\left({\frac {\sqrt {2}}{2}}\right)\left(-{\frac {\sqrt {2}}{2}}\right)\\-\left({\frac {\sqrt {2}}{2}}\right)\left(-{\frac {\sqrt {2}}{2}}\right)&-\left(-{\frac {\sqrt {2}}{2}}\right)^{2}&\left({\frac {\sqrt {2}}{2}}\right)\left(-{\frac {\sqrt {2}}{2}}\right)&\left(-{\frac {\sqrt {2}}{2}}\right)^{2}\end{bmatrix}}={\begin{bmatrix}{2.5}&{-2.5}&{-2.5}&{2.5}\\{-2.5}&{2.5}&{2.5}&{-2.5}\\{-2.5}&{2.5}&{2.5}&{-2.5}\\{2.5}&{-2.5}&{-2.5}&{2.5}\end{bmatrix}}\end{aligned}}$

Global Node Coordinates

Global node 1

$\displaystyle {\begin{aligned}&(x_{1}^{(1)},y_{2}^{(1)})\\&x_{1}^{(1)}=-L^{(1)}\cos \theta ^{(1)}=-\cos 30^{\circ }=-2{\sqrt {3}}\\&y_{2}^{(1)}=-L^{(1)}\sin \theta ^{(1)}=-\sin 30^{\circ }=-2\\&(-2{\sqrt {3}},-2)\end{aligned}}$

Global node 3

$\displaystyle {\begin{aligned}&(x_{3}^{(2)},y_{4}^{(2)})\\&x_{3}^{(2)}=-L^{(2)}\cos \theta ^{(2)}=\cos -45^{\circ }={\sqrt {2}}\\&y_{4}^{(2)}=-L^{(2)}\sin \theta ^{(2)}=\sin -45^{\circ }=-{\sqrt {2}}\\&({\sqrt {2}},-{\sqrt {2}})\end{aligned}}$

On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.

Problem R1.4: 2D Truss System with MATLAB

Given

Consider a plane truss consisting of tree bars with the properties E = 200 GPa, A₁ = 6.0 · 10^-4 m², A₂ = 3.0 · 10^-4 m² and A₃ = 10.0 · 10^-4 m², and loaded by a single force P = 80 kN. The corresponding finite element model consists of three elements and eight degrees of freedom.

Find

Analyze the 2-D truss system utilizing the CALFEM toolbox in MATLAB.

Solution

The finite element model (shown below) matching the truss is made up of eight degrees of freedom and three elements.

The topology matrix, Edof, is calculated to be

Edof=

[1 1 2 5 6;

2 5 6 7 8;

3 3 4 5 6];

K, a global stiffness matrix, and f, a load vector, are defined. The load P is separated into x and y components then inserted in proper location in the load vector f.

K=zeros(8); f=zeros(8,1);  f(6)=-80e3;

The element property vectors ep1, ep2 and ep3 are defined by

E=2.0e11;  A1=6.0e-4;  A2=3.0e-4;  A3=10.0e-4;  ep1=[E A1]; ep2=[E A2]; ep3=[E A3];

The element coordinate vectors ex1, ex2, ex3, ey1, ey2 and ey3 are defined by

ex1=[0 1.6];  ex2=[1.6 1.6];  ex3=[0 1.6];  ey1=[0 0];  ey2=[0 1.2];  ey3=[1.2 0];

The function bar2e from the CALFEM toolbox is used to compute the element matrices, Ke. The global stiffness matrix is then created using the function assem, integrating these element matrices.

Ke1=bar2e(ex1,ey1,ep1)

Ke1 =

1.0e+007 *

7.5000   0  -7.5000   0

  0      0     0      0

-7.5000  0   7.5000   0

  0      0     0      0

Ke2=bar2e(ex2,ey2,ep2)

Ke2 =

1.0e+007 *

0       0     0     0

0    5.0000   0  -5.0000

0       0     0     0

0   -5.0000   0   5.0000

Ke3=bar2e(ex3,ey3,ep3)

Ke3 =

1.0e+007 *

6.4000    -4.8000   -6.4000    4.8000

-4.8000    3.6000    4.8000   -3.6000

-6.4000    4.8000    6.4000   -4.8000

4.8000    -3.6000   -4.8000    3.6000

The bar2e function takes the element node coordinates, young’s modulus, and cross section area and creates a 4x4 stiffness matrix for a 2-D bar element. This is done using the following script.

E=ep(1);

A=ep(2);

b=[ex(2) -ex(1); ey(2) -ey(1)];

L=sqrt(b'*b);

Kle=E*A/L*[1 -1; -1  1];

n=b'/L;

G=[n  zeros(size(n)); zeros(size(n))  n];

Ke=G'*Kle*G;

Based on the topology information, the global stiffness matrix can be generated by assembling the element stiffness matrices

K=assem(Edof(1,:),K,Ke1);

K=assem(Edof(2,:),K,Ke2);

K=assem(Edof(3,:),K,Ke3)

K =

1.0e+008 *

0.7500       0        0          0        -0.7500        0          0       0

   0         0        0          0           0           0          0       0

   0         0      0.6400    -0.4800     -0.6400      0.4800       0       0

   0         0     -0.4800     0.3600      0.4800     -0.3600       0       0

-0.7500      0     -0.6400     0.4800      1.3900     -0.4800       0       0

   0         0      0.4800    -0.3600     -0.4800      0.8600       0    -0.5000

   0         0        0         0            0           0          0       0

   0         0        0         0            0        -0.5000       0     0.5000

The assem function uses this script to assemble element matrices Ke and fe into the global stiffness matrix K and global force vector f according to the topology matrix edof. The script takes in the edof, K, Ke, f, and fe and puts out the K and f matrix and vector, respectively.

[nie,n]=size(edof);

    t=edof(:,2:n);

    for i = 1:nie

      K(t(i,:),t(i,:)) = K(t(i,:),t(i,:))+Ke;

      if nargin==5

         f(t(i,:))=f(t(i,:))+fe;

      end

    end

Using the following loop, the element matrices are computed and assembled.

for  i=1:10

    Ke=bar2e(Ex(i,:),Ey(i,:),ep);

    K=assem(Edof(i,:),K,Ke);

end;

The displacements a and the support forces r are computed by solving the system of equations considering the prescribed displacements in bc. This is done using the solveq function.

bc= [1 0;2 0;3 0;4 0;7 0;8 0];

[a,r]=solveq(K,f,bc)

a =

1.0e-002 *

0

0

0

0

-0.0398

-0.1152

0

0

r =

1.0e+004 *

2.9845

0

-2.9845

2.2383

0.0000

0.0000

0

5.7617

The solveq function uses this script to solve the system of equations and puts the results in a global displacement matrix and reaction force matrix.

if nargin==2 ;

     d=K\f ;

  elseif nargin==3;

     [nd,nd]=size(K);

     fdof=[1:nd]';

     d=zeros(size(fdof));

     Q=zeros(size(fdof));

     pdof=bc(:,1);

     dp=bc(:,2);

     fdof(pdof)=[];

     s=K(fdof,fdof)\(f(fdof)-K(fdof,pdof)*dp);

     d(pdof)=dp;

     d(fdof)=s;

  end

     Q=K*d-f;

The results of a show that the displacement at the point of loading is 1.15 mm in the y-direction. The section forces es1, es2 and es3 are calculated using bar2s from element displacements ed1, ed2 and ed3, which are obtained using extract. The element displacements are used to evaluate normal forces. The extract function obtains the global displacements from the Edof and a matrices, and the normal forces are evaluated using the bar2s function.

ed1=extract(Edof(1,:),a);

N1=bar2s(ex1,ey1,ep1,ed1)

N1 =

-2.9845e+004

ed2=extract(Edof(2,:),a);

N2=bar2s(ex2,ey2,ep2,ed2)

N2 =

5.7617e+004

ed3=extract(Edof(3,:),a);

N3=bar2s(ex3,ey3,ep3,ed3)

N3 =

3.7306e+004

Therefore, the normal forces are N1 = −29.84 kN, N2 = 57.62 kN and N3 = 37.31 kN.

On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.

Problem R1.5: Damping Comparisons

Given

Consider the spring-mass damper system on p.53-2, and the following cases for the roots of the characteristic equations.

1. $\lambda _{1}=-0.5,\lambda _{2}=-1.5$
2. $\lambda _{1}=\lambda _{2}=-0.5$
3. $\lambda _{1}=-0.5+i2,\lambda _{2}=-0.5-i2$

Initial Conditions:

$y(0)=1,y'(0)=0$

Case 1: Overdamped

$\Delta =a^{2}-4b>0$
$(\lambda +0.5)(\lambda +1.5)=0$
$\lambda ^{2}+4\lambda +0.75=0$

Therefore L2-ODE-CC:
$y_{h}''+4y_{h}'+0.75y_{h}=0$

Find

Derive the overdamped L2-ODE-CC and the overall homogeneous solution.

Solution

$y=C_{1}e^{(\lambda _{1}x)}+C_{2}e^{(\lambda _{2}x)}$
$y=C_{1}e^{(-0.5x)}+C_{2}e^{(-1.5x)}$ ............... (1)
$y'=-0.5C_{1}e^{(-0.5x)}+(-1.5)C_{2}e^{(-1.5x)}$ .............(2)

Using the two initial conditions and solving equation (1) and (2) the coefficients are as follows: $C_{1}=1.5,C_{2}=-0.5$

Therefore,
$y=1.5e^{(-0.5x)}+-0.5e^{(-1.5x)}$

Case 2: Critically damped

$\Delta =a^{2}-4b=0$
$(\lambda +0.5)(\lambda +0.5)=0$
$\lambda ^{2}+\lambda +0.25=0$

Therefore L2-ODE-CC:
$y_{h}''+y_{h}'+0.25y_{h}=0$

Find

Derive the critically damped L2-ODE-CC and the overall homogeneous solution.

Solution

$y=C_{1}e^{(\lambda _{1}x)}+C_{2}xe^{(\lambda _{2}x)}$
$y=C_{1}e^{(-0.5x)}+C_{2}xe^{(-0.5x)}$ ............... (3)
$y'=-0.5C_{1}e^{(-0.5x)}+(-0.5)C_{2}xe^{(-0.5x)}+C_{2}e^{(-0.5x)}$ .............(4)

Using the two initial conditions and solving equation (3) and (4) the coefficients are as follows: $C_{1}=2/3,C_{2}=1/3$

Therefore,
$y=(2/3)e^{(-0.5x)}+(1/3)xe^{(-0.5x)}$

Case 3: Underdamped

$\Delta =a^{2}-4b<0$
$\alpha =-0.5,\beta =2$
$(\lambda -(-0.5+2i))(\lambda -(-0.5-2i))=0$
$\lambda ^{2}+1\lambda +2.25=0$

Therefore L2-ODE-CC:
$y_{h}''+y_{h}'+2.25y_{h}=0$

Find

Derive the underdamped L2-ODE-CC and the overall homogeneous solution.

Solution

$y=C_{1}e^{(\alpha x)}cos(\beta x)+C_{2}e^{(\alpha x)}sin(\beta x)$
$y=C_{1}e^{(-0.5x)}cos(2x)+C_{2}e^{(-0.5x)}sin(2x)$ ......... (5)
$y'=-0.5C_{1}e^{(-0.5x)}cos(2x)-2C_{1}e^{(-0.5x)}sin(2x)-0.5C_{2}e^{(-0.5x)}sin(2x)+2C_{2}e^{(-0.5x)}cos(2x)$ ......(6)

Using the two initial conditions and solving equation (5) and (6) the coefficients are as follows: $C_{1}=1,C_{2}=.25$

Therefore,
$y=e^{(-0.5x)}cos(2x)+0.25e^{(-0.5x)}sin(2x)$

Comparison Graph

On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.

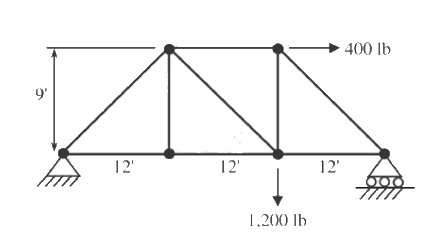
R1.6 Element Stiffness Matrices in MATLAB and Force Solution by hand

Given

Member Profile:

Young’s Modulus: E = 100,000 psi (for all members)

All cross-sections are circular: D = 2 inches, A = 0.0218 feet

Find

Write a MATLAB program to compute the element stiffness matrices for all elements in this truss system; Do a hand calculation to find all member forces (fig on p.104), using your knowledge in Statics and Mechanics of Materials.

Solution

Part A: Obtain Element Stiffness Matrices in MATLAB

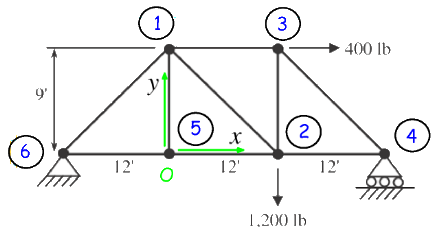
Step 1 Define Coordinate System and Global Node Numbering

The origin is placed at node 5. Global nodes are arbitrarily numbered to demonstrate the power of the direct finite element method. No matter how the solver decides to label his system, the results will come out correct.

Step 2 Define Element Numbering

Once again, element numbering has been arbitrarily placed for demonstrative purposes.

Step 3 Create Truss in MATLAB using CALFEM

CALFEM (Computer Aided Learning of the Finite Element Method) is a Finite Element Method Toolbox for use within MATLAB. It is a collection of functions to assist the user in quickly implementing the finite element method (FEM) to their problems.

For the purposes of solving element stiffness matrices, CALFEM has a handy function in the toolbox named bar2e.

Download the CALFEM toolbox here: http://sourceforge.net/projects/calfem/

CALFEM Documentation: http://www.solid.lth.se/fileadmin/hallfasthetslara/utbildning/kurser/FHL064_FEM/calfem34.pdf

Bar2e Description

bar2e produces a global element stiffness matrix Ke for a 2-D bar element.

Bar2e

MATLAB Syntax

Ke=bar2e(ex,ey,ep)

The input variables

supply the element’s nodal coordinates x1, y1, x2, and y2, and the relevant properties of the element: the modulus of elasticity E and the cross section area A.

Theory

The element stiffness matrix , stored in Ke, is computed according to

where

The transformation matrix contains the direction cosines

where the length

Putting It All Together

With the defined coordinate system, and numbered global nodes and elements, the truss system can be made in MATLAB.

Problem6TrussSolver.m Code:

%Report 1 Problem 6

ep = [10^4 (pi/4*(1/6)^2)]; % [E A], E is in psi, A is in feet

%Origin defined at Node 2

%Element 1  ---Global Nodes 5 and 2

e1x = [0 12]; %[x1 x2] x1,y1 refers to local node 1

e1y = [9 0]; %[y1 y2] x2,y2 referes to local node 2

%Element 2  ---Global Nodes 6 and 1

e2x = [12 24]; 

e2y = [9 0]; 

%Element 3  ---Global Nodes 3 and 2

e3x = [12 24]; 

e3y = [0 0]; 

%Element 4  ---Global Nodes 2 and 4

e4x = [0 0]; 

e4y = [9 0]; 

%Element 5  ---Global Nodes 5 and 6

e5x = [0 12]; 

e5y = [0 0]; 

%Element 6  ---Global Nodes 3 and 4

e6x = [-12 0]; 

e6y = [0 0]; 

%Element 7  ---Global Nodes 1 and 5

e7x = [0 12]; 

e7y = [9 9];

%Element 8  ---Global Nodes 1 and 2

e8x = [-12 0]; 

e8y = [0 9]; 

%Element 9  ---Global Nodes 1 and 3

e9x = [12 12]; 

e9y = [9 0]; 

%computing stiffness matrices

Ke1 = bar2e(e1x,e1y,ep);

Ke2 = bar2e(e2x,e2y,ep);

Ke3 = bar2e(e3x,e3y,ep);

Ke4 = bar2e(e4x,e4y,ep);

Ke5 = bar2e(e5x,e5y,ep);

Ke6 = bar2e(e6x,e6y,ep);

Ke7 = bar2e(e7x,e7y,ep);

Ke8 = bar2e(e8x,e8y,ep);

Ke9 = bar2e(e9x,e9y,ep);

%puts all element matrices on display within MATLAB

display(Ke1);

display(Ke2);

display(Ke3);

display(Ke4);

display(Ke5);

display(Ke6);

display(Ke7);

display(Ke8);

display(Ke9);

The output of R1P6.m:

>> run R1P6.m

Ke1 =

    9.3084   -6.9813   -9.3084    6.9813

   -6.9813    5.2360    6.9813   -5.2360

   -9.3084    6.9813    9.3084   -6.9813

    6.9813   -5.2360   -6.9813    5.2360

Ke2 =

    9.3084   -6.9813   -9.3084    6.9813

   -6.9813    5.2360    6.9813   -5.2360

   -9.3084    6.9813    9.3084   -6.9813

    6.9813   -5.2360   -6.9813    5.2360

Ke3 =

   18.1805         0  -18.1805         0

         0         0         0         0

  -18.1805         0   18.1805         0

         0         0         0         0

Ke4 =

         0         0         0         0

         0   24.2407         0  -24.2407

         0         0         0         0

         0  -24.2407         0   24.2407

Ke5 =

   18.1805         0  -18.1805         0

         0         0         0         0

  -18.1805         0   18.1805         0

         0         0         0         0

Ke6 =

   18.1805         0  -18.1805         0

         0         0         0         0

  -18.1805         0   18.1805         0

         0         0         0         0

Ke7 =

   18.1805         0  -18.1805         0

         0         0         0         0

  -18.1805         0   18.1805         0

         0         0         0         0

Ke8 =

    9.3084    6.9813   -9.3084   -6.9813

    6.9813    5.2360   -6.9813   -5.2360

   -9.3084   -6.9813    9.3084    6.9813

   -6.9813   -5.2360    6.9813    5.2360

Ke9 =

         0         0         0         0

         0   24.2407         0  -24.2407

         0         0         0         0

         0  -24.2407         0   24.2407

Part B: Hand Calculation of Force in Each Member

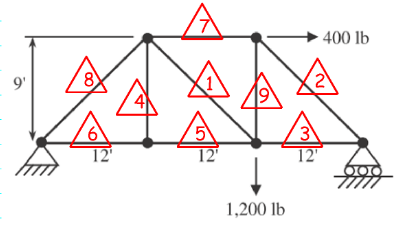
Step 1: Solve for Majority of Force Members by Method of Sections

The method of sections is a great tool for solving statics problems. By isolating certain forces, forces can be immediately solved for as long as there are three or less unknown forces within the section cut.

Starting a truss problem with the method of sections is typically a faster method for truss problems. After a majority for the forces are found, the remaining minority can be quickly calculated with the method of joints.

Method of Sections Part 1

Method of Sections Part 2

Step 2: Method of Joints

The method of joints isolates a single point in the truss system. With the use of a free body diagram, unknown forces can quickly be solved.

Method Of Joints

On our honor, we did this assignment on our own, without looking at the solutions in previous semesters or other online solutions.