University of Florida/Egm6341/s11.team1.Gong/Mtg22

Mtg 30: Mon, 14 Mar 11

page22-1 Comp. Trap. rule error: $h={\color {red}{\frac {\color {black}(b-a)}{n}}}{\color {blue}\leftarrow }{\color {red}(3)}{\color {blue}p.7-4}$ ${E}_{n}^{\color {blue}T(Trap.)}{\underset {{\color {red}(1)}{\color {blue}p.7-4}}{:=}}\ I-{I}_{n}^{T}=\int _{a}^{b}f(x)dx-h[{\color {red}{\frac {1}{2}}}f(x_{\color {red}0})+f(x_{1})+\cdots +f(x_{n-1}){\color {red}{\frac {1}{2}}}f(x_{\color {red}n})]\ {\color {red}(1)}$ $=\sum _{i=1}^{n}{\color {blue}\left\{{\color {black}\int _{x_{i-1}}^{x_{i}}f(x)dx-{\frac {h}{2}}[f(x_{i-1})+f(x_{i})]}\right\}}$ (1)p.17-2: $\left|{E}_{n}^{T}\right|\leqslant {\frac {h^{3}}{12}}{\underset {\color {blue}{\underset {\overset {\color {red}(3)}{=:{\overline {M_{2}}}}}{\color {blue}\underbrace {\color {black}\xi \in ]x_{i-1},x_{i}[} }}}{\sum _{i=1}^{n}(max{\color {red}\left|{\color {black}f^{\color {blue}(2)}(\xi )}\right|})}}{\color {red}\ (2)}$ (4)p.17-1: ${\overline {M_{2}}}\leqslant M_{2}\ {\color {red}(4)}$ $\left|{\color {blue}{\color {black}E}_{n}^{T}}\right|\leqslant {\frac {(b-a)^{3}}{12n^{3}}}nM_{2}={\frac {(b-a)^{3}}{12{\color {blue}n^{2}}}}M_{2}={\frac {(b-a)h^{\color {red}2}}{12}}M_{2}$ ${\color {blue}A.P.253}$ ${\color {red}(5)}$ page22-2 HW*4.8: Comp. Simpson error $\left|{E}_{\color {blue}n}^{\color {blue}S}\right|\leqslant {\frac {(b-a)^{5}}{2880n^{4}}}{\color {blue}{\underset {{\color {red}(4)}p.17-1}{\underbrace {\color {black}M_{4}} }}}={\frac {(b-a)h^{\color {red}(4)}}{2880}}M_{4}\ \color {red}(1)$ HW*4.8: See HW*2.4 p.7-3 1) Use error estimate for Taylor Series, Compare Trap., Compare Simpson, to findn Q(10-6), and compare to number results. 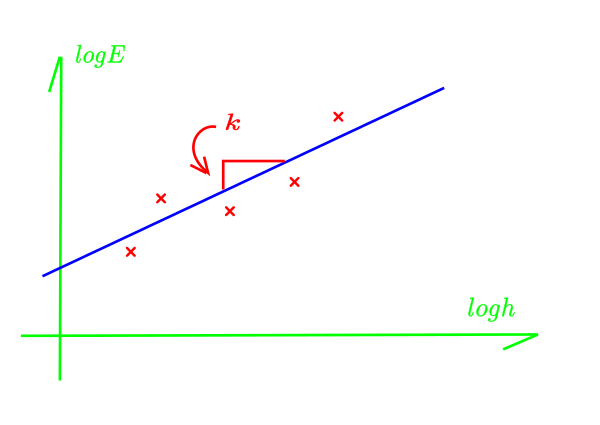2)Numerically find the power ofhin error : Plot logerror vslogh , and meas. slop with least square (lin. regression).   $E=ah^{\color {red}k}+Q(h^{k+1}),\$ $\ logE=loga+{\color {red}k}logh$ page22-3 HW*4.9: pf. of SSET, G(.) in (1) p.19-1 A)Redo the pf for 2 cases ${\color {blue}1)}\ G(t):=\ e(t)-t^{\color {red}4}e(1)\ {\color {red}(1)}$ ${\color {blue}2)}\ G(t):=\ e(t)-t^{\color {red}6}e(1)\ {\color {red}(2)}$ Print out where pf breaks down. B)For G(t) as in(1)p.19-1(w/t5), find G(3)(0)  and follow same steps in pf to see what happen.   HW*4.10:1)Don'tUse matlabtrapz forcompare Trap.in your code to produce Table 5.1 n A.p.255(p.22-4)   ${\color {red}(3)}I=\int _{0}^{\pi }e^{x}{\color {blue}sinx}dx$(use WAto find I)