EGM6321 - Principles of Engineering Analysis 1, Fall 2009
[edit | edit source]Mtg 15: Thur, 24Sept09
Ex.1 P.14-4 :
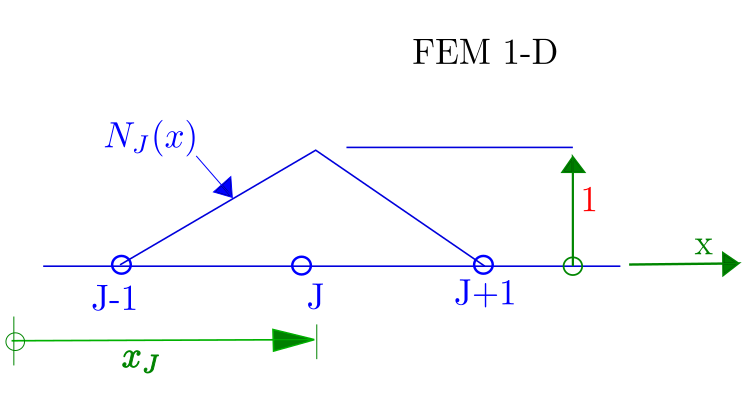
 finite element basis function associated with node J = "hat" function.
finite element basis function associated with node J = "hat" function.
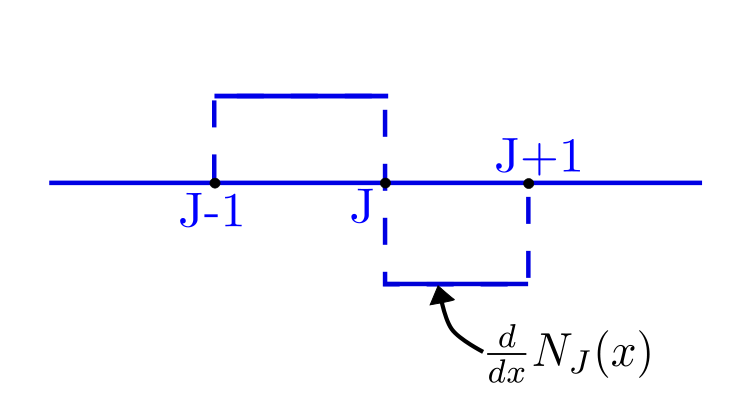
 , but
, but 
Ex.1 P.14-4 : Cubic Spline (Bexler, cubic Hermitian)

Cubic  4 Coefficients
4 Coefficients  4 degrees of freedom per element
4 degrees of freedom per element  2 degrees of freedom per node (each element has 2 nodes)
2 degrees of freedom per node (each element has 2 nodes)

HW:  , but
, but  , for
, for 

 ,
, 

 , where A and B are constants
, where A and B are constants
Where this can be rewritten for x as:  , where A and B are constants
, where A and B are constants

Euler Equations: Special Homogeneous Ln_ODE_VC

Where  and
and 
Two methods of solution:
Method 1: Transfer of variables 
Method 2: Method of undetermined coefficients 
(Or Trial Solution) K.etal(2003)






















