Report 5
Find  for the following series:
for the following series:
1. 
2. 

Use (2)-(3)p.7-31 to find  for the Taylor series of
for the Taylor series of
3.  at
at 
4.  at
at 
5.  at
at 
1. 
Using L'Hospital's rule and (2)p.7-31, and setting  :
:
![{\displaystyle R_{c}=\left[\lim _{k\to \infty }\left|{\frac {(k+2)(k+1)}{(k+1)k}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {k+2}{k}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {1}{1}}\right|\right]^{-1}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d89ec676f3cf615faaeb0997172dcb95b74783ba)
2.
Using (3)p.7-31 and setting  :
:
![{\displaystyle R_{c}=\lim _{k\to \infty }\left[{\sqrt[{k}]{\left|{\frac {(-1)^{k}}{\gamma ^{k}}}\right|}}\right]^{-1}=\lim _{k\to \infty }{\frac {{\sqrt[{k}]{|\gamma ^{k}}}|}{\sqrt[{k}]{|(-1)^{k}|}}}=\lim _{k\to \infty }{\frac {\sqrt {|\gamma |}}{\sqrt {|-1|}}}={\sqrt {|\gamma |}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf4cb5edaa63bfb91ef61971c7b7d8f627d672ad)
3. Taylor series about  :
:

Using (2)p.7-31 and setting  :
:
![{\displaystyle R_{c}=\left[\lim _{k\to \infty }\left|{\frac {\frac {(-1)^{k+1}}{(2(k+1)+1)!}}{\frac {(-1)^{k}}{(2k+1)!}}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {-1}{(2k+3)(2k+2)}}\right|\right]^{-1}=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b721fc0efcd52911cf42fc70932fb7c8ddeaf4d9)
4. Taylor series about  :
:

Using L'Hospital's rule and (2)p.7-31, and setting  :
:
![{\displaystyle R_{c}=\left[\lim _{k\to \infty }\left|{\frac {\frac {(-1)^{k+1}}{(k+2)}}{\frac {(-1)^{k}}{(k+1)}}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {(-1)(k+1)}{(k+2)}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {-1}{1}}\right|\right]^{-1}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cd4a14cdb511abf7e3c8034eb8ea2b23678a9e9)
5. Taylor series about  :
:

Using L'Hospital's rule and (2)p.7-31, and setting  :
:
![{\displaystyle R_{c}=\left[\lim _{k\to \infty }\left|{\frac {\frac {(-1)^{k+2}}{(k+1)2^{k+1}}}{\frac {(-1)^{k+1}}{k2^{k}}}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {-1k}{2(k+1)}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {-1}{2}}\right|\right]^{-1}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6e30324a52fa7ec79718228b79c6a2b784f05b6)
This problem is solved and uploaded by Radina Dikova
Determine whether the following pairs of functions are linearly independent:


First use the Wronskian method, then use the Gramian method.
The Wronskian is defined as: 
If  , then the functions f and g are linearly independent.
, then the functions f and g are linearly independent.
The Gramian is defined as: 
Where 
If  , then the functions f and g are linearly independent.
, then the functions f and g are linearly independent.
1. Using Wronskian.

Therefore, f and g are linearly independent.
2. Using Wronskian.

Therefore, f and g are linearly independent.
1. Using Gramian with an interval of [-1,1]




Therefore, f and g are linearly independent.
2. Using Gramian with an interval of [-1,1]




Therefore, f and g are linearly independent.
This problem was solved and uploaded by David Herrick.
Verify that  and
and  in (1)-(2) p.7-34 are linearly independent using the Gramian
in (1)-(2) p.7-34 are linearly independent using the Gramian
The given Grammian:
|

|
In reference to to (3) on p.8-9
|

|
Calculating the dot products yields:
|

|
|
|

|
|
|

|
|
|

|
Plugging the dot products into the Grammian yields:
|

|
Therefore, b1 and b2 are linearly independent.
Solved and uploaded by Derik Bell
Show that:

is the particular solution to:

Discuss the choice of particular solutions in the table on p8-3. In other words, for r(x) = kcos(wx), why would you need to have both cos(wx) and sin(wx) in the particular solution?
For a single excitation that satisfies
 ,
,

for example:



and so on until...
 where by linearity:
where by linearity:

Since  is the solution to a single iteration of r(x) and
is the solution to a single iteration of r(x) and  , then by linearity, the solution to r(x) is:
, then by linearity, the solution to r(x) is:

Part 2:
kcos(wx) is a periodic function. As shown by (3) on p8-2, any periodic function can be broken down into a fourier trigonometric series:
![{\displaystyle r(x)=a_{0}+\sum _{n=1}^{\infty }[a_{n}cos(nwx)+b_{n}sin(nwx)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/858d13ad529622b5ebcfb7acfaed39dd0e53bec5)
r(x) can be further broken down as the sum of:



Where 
Since r(x) is expressed in terms of cos(x) and sin(x) the particular solution, which is also a sum of the individual particular solutions for each iteration of  ,
,  , and
, and  , needs to be in terms of sin(x) and cos(x) as well. That applies to all periodic functions as shown on p8-2, which sin(x) is as well. Therefore that justifies why the particular solutions for kcos(wx), ksin(wx),
, needs to be in terms of sin(x) and cos(x) as well. That applies to all periodic functions as shown on p8-2, which sin(x) is as well. Therefore that justifies why the particular solutions for kcos(wx), ksin(wx),  , and
, and  must all include both cos(x) and sin(x).
must all include both cos(x) and sin(x).
This problem was solved and uploaded by John North.
- 1. Show that cos(7x) and sin(7x) are linearly independent using the Wronskian and the Gramian (integrate over 1 period)
- 2. Find 2 equations for the two unknowns M,N and solve for M,N
- 3. Find the overall solution y(x) that corresponds to the initial condition y(0)=1, y'(0)=0. Plot the solution over 3 periods.
(1)
First, using Wronskian:
- For 2 functions, f and g, the Wrosnkian is defined as

- Where f and g are linearly independent if

- For

- Then,

Therefore, f and g are linearly independent
Second, using Gramian:
- Consider two functions, f and g, where the scalar product is defined as

- And the Gramian defined as

- Then f and g are linearly indepdent if

- For f=cos(7x) and g=sin(7x) and integrating over one period (
 )
)

- Letting
 and changing limits of integration by plugging in old limits into "u" equation
and changing limits of integration by plugging in old limits into "u" equation
![{\displaystyle \displaystyle <f,f>={\frac {1}{7}}\int _{0}^{2\pi }cos^{2}(u)du={\frac {1}{7}}[{\frac {u}{2}}+{\frac {1}{4}}sin2u\mathbf {\mid } _{0}^{2\pi }]={\frac {\pi }{7}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/263cce7ecd18acb9ddad438083778f296463e589)

- Letting
 and changing the limits of integration by plugging in old limits into "u" equations
and changing the limits of integration by plugging in old limits into "u" equations
![{\displaystyle \displaystyle <g,g>={\frac {1}{7}}\int _{0}^{2\pi }sin^{2}(u)du={\frac {1}{7}}[{\frac {u}{2}}-{\frac {1}{4}}sin2u\mid _{0}^{2\pi }]={\frac {\pi }{7}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97164633c3a9ffc4faef325b4d92790d7a003655)

- From Kreyszig p.479, it is apparent that sin and cos are orthogonal to each other, so the above integration will equal zero

- Plugging in the results of each integral into the Gramian

Therefore, f and g are linearly independent
(2)
- Given

- And particular solutions of the form

- Plug particular solutions back into original ODE and collect like terms


- Equating coefficients



(3)
The overall solution  consists of the particular solution and homogeneous soloution
consists of the particular solution and homogeneous soloution
- Homogeneous solotuion

 so we have distinct real roots
so we have distinct real roots
![{\displaystyle \displaystyle \lambda _{1,2}={\frac {1}{2}}[-a\pm {\sqrt {a^{2}-4b}}]={\frac {1}{2}}[3\pm 7]=5,-2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32fd38fa7576045718896b24a05d4d968d62122a)

- Using initial conditions
 and
and 


- Solving the two equations for the two unknowns yields


- Particular solution
 where
where 

- Giving us an overall solution of

- Plotting the solution over three periods

Matlabcode
EDU>> x=0:0.001:(6*pi)/7;
EDU>> y=(2/7).*exp(5.*x)+(5/7).*exp(-2.*x)-(3/59).*cos(7.*x)-(1/7).*sin(7.*x);
EDU>> plot(x,y)
Solved and uploaded by Joshua House
Find the solution to the following initial condition problem, and plot it over 3 periods.




First, we take the first and second derivative of the particular solution:
![{\displaystyle \displaystyle y'_{p}(x)=e^{-2x}(-3Msin(3x)-2Mcos(3x)+3Ncos(3x)-2Nsin(3x))=e^{-2x}[(-3M-2N)sin(3x)+(-2M+3N)cos(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57e59630b7409a345dd5ea03e26e6d0f9b73fb4c)

![{\displaystyle \displaystyle =2e^{-2x}[(12M-5N)sin(3x)+(13M-12N)cos(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d81b8e488e32c288d1f54bd36e45d78239afe306)
Now, we plug the particular solution derivatives into the initial equation:

![{\displaystyle \displaystyle 2e^{-2x}[(12M-5N)sin(3x)+(13M-12N)cos(3x)]+4[e^{-2x}[(-3M-2Nsin(3x)+(-2M+3N)cos(3x)]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95d75df2a5f12657a53a39da5862f3186f89477b)
![{\displaystyle \displaystyle +13[e^{-2x}[Mcos(3x)+Nsin(3x)]]=2e^{-2x}cos(3x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f6418320a09c5c1ee69e9763e80550a195079ef)
![{\displaystyle \displaystyle e^{-2x}[(24M-10N)sin(3x)+(26M-24N)cos(3x)+(-12M-8N)sin(3x)+(-8M+12N)cos(3x)+13Mcos(3x)+13Nsin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cea19074022c2229385c5047fb58f026dcbb239)


Now, we equate the coefficients of sin(3x) and cos(3x) to determine the unknown coefficients M and N:



Therefore, the particular solution is:
![{\displaystyle \displaystyle y_{p}(x)=e^{-2x}[{\frac {10}{11}}cos(3x)+{\frac {24}{11}}sin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bb9afdf7616bf58cccd80df8b554b97d149bbb1)
Now, we focus on the homogeneous part of the solution. It is given to us as:
![{\displaystyle \displaystyle y_{h}(x)=e^{-2x}[Acos(3x)+Bsin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b76122f69f374297e69cd0733255c40882d7b3)
As you can see, this is identical to the particular solution, except that M is now A and N is now B. Therefore, the first derivative of the homogenous solution will be in the same form as the first derivative of the particular solution:
![{\displaystyle \displaystyle y'_{h}(x)=e^{-2x}(-3Asin(3x)-2Acos(3x)+3Bcos(3x)-2Bsin(3x))=e^{-2x}[(-3A-2B)sin(3x)+(-2A+3B)cos(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e97310806a2ca538f50780255d53f3439bf777a1)
Remembering the two initial conditions, y(0) = 1 and y'(0) = 0, we apply these to the homogenous equations:
![{\displaystyle \displaystyle y_{h}(0)=e^{-2x}[Acos(3x)+Bsin(3x)]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffc00dbfda6b2c926f9884abe6d7001a1e53b9db)
![{\displaystyle \displaystyle y'_{h}(x)=e^{-2x}[(-3A-2B)sin(3x)+(-2A+3B)cos(3x)]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/619688406e79bb47ca01d1ea36d30112ad8d50c8)
This yields two equations that we can use to solve for the coefficients A and B:


Therefore, the homoegenous solution is:
![{\displaystyle \displaystyle y_{h}(x)=e^{-2x}[cos(3x)+{\frac {3}{2}}sin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff17ff2c1c6abd9c59f0c16cd6a120ee0aeb919)
We find the final solution, y(x), by adding the homogenous and particular solutions as seen below:
![{\displaystyle \displaystyle y(x)=y_{h}(x)+y_{p}(x)=e^{-2x}[cos(3x)+{\frac {3}{2}}sin(3x)]+e^{-2x}[{\frac {10}{11}}cos(3x)+{\frac {24}{11}}sin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ecacb10a8174f4c79a42670677353930f528306)
![{\displaystyle \displaystyle y(x)=e^{-2x}[{\frac {21}{11}}cos(3x)+{\frac {81}{22}}sin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/254db9075f5b197df5ac99cca8b1d36b5819af19)
Matlab Code:
x= 0:0.001:(2*pi/3);
y = exp(-2.*x)*(21/11).*cos(3.*x) + exp(-2.*x)*(81/22).*sin(3.*x);
plot(x,y)
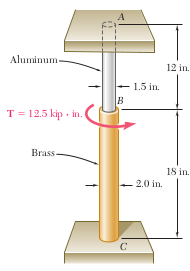
This problem was solved and uploaded by Will Knapper

The oblique basis vectors are:


1. Find the components  using the Gram matrix as in (1)p.8-11.
using the Gram matrix as in (1)p.8-11.
2. Verify the results by using (1)-(2)p.7c-34 in (2)p8-11, and rely on the non-zero determinant of the matrix of components of  relative to the basis
relative to the basis  , as discussed on p.7c-34.
, as discussed on p.7c-34.
1. Using Gram matrix as in (1) p.8-10:

 =
= 
From (3)p.8-9 we know that  . Solving the various components we get:
. Solving the various components we get:

 =
= 
In order to solve for  we need to calculate the inverse of
we need to calculate the inverse of  .
.
This gives is the Gram matrix as used in (1)p.8-11:


 =
= 
Thus:

2. Plugging in  into
into  we get:
we get:



Separating into components:
 and
and 
Solving the two linearly independent equations we get:


This problem was solved and uploaded by Radina Dikova
Find the integral (see R5.9)

using integration by parts and then with the help of General binomial theorem.


The indefinite integral of  is
is

For n = 0, we get 
For n = 1, we get 
And the indefinite integral of  is
is

Integration by parts
- For n = 0
![{\displaystyle \ \int x^{0}log(1+x)dx=log(1+x)[x+1]-x\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f3609807f317cef95c4cdcd1d0d90d3896fdb7a)
- For n = 1
![{\displaystyle \ \int x^{1}log(1+x)dx={\frac {1}{2}}*[(x-log(1+x))+x^{2}log(1+x)-{\frac {x^{2}}{2}}]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e372b7cb59ec182b8614199a2e07058daa0bf49)
Solved and uploaded by
Mike Wallace
Consider the L2-ODE-CC(5)p.7b-7 with log(1+x) as excitation:


and the initial conditions

Project the excitation r(x) on the polynomial basis
![{\displaystyle \ [b_{j}(x)=x^{j},j=0,1,...,n]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dc72c6a0e4fd696b1058039ce8110ad77653a7a)
i.e., find  such that
such that
r(x) ≈ 
for x in ![{\displaystyle \ [-{\frac {3}{4}},3],\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb66d40d4df2c944438f22654e25df8b28a2adeb) and for n = 3, 6, 9
and for n = 3, 6, 9
Plot  to show uniform approximation and convergence
to show uniform approximation and convergence
In a separate series of plots, compare the approximation of the function log(1+x) by 2 methods:
A. Projection on polynomial basis (1) p.8-17
B. Taylor series expansion about x = 0
Observe and discuss the pros and cons of each method
Find  such that:
such that:

with the same initial conditions (2) p.7c-28
Plot  for n = 3, 6, 9, for x in
for n = 3, 6, 9, for x in ![{\displaystyle \ [-{\frac {3}{4}},3].\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/688918f3fdad89b20488740db39ba67f3bdfc4a6)
In a series of separate plots, compare the results obtained with the projected excitation on polynomial basis to those with truncated Taylor series of the excitation. Plot also the numerical solution as a baseline for comparison.
Using

For n = 0










Subtracting Y from Y' in order to find the coefficients



For n = 0 the final solution will be

For n = 1

We need to find the homogeneous Y




Solving for the initial conditions



This gives coefficients of:

For n = 1 the final solution will be;

This problem was solved and uploaded by
Mike Wallace
Problem 2 was solved and Problem 5 was proofread by David Herrick
Problem 5 was solved and uploaded by Joshua House
Problems 1 and 7 were solved and uploaded by Radina Dikova
Problem 3 was solved and uploaded by Derik Bell
Problem 4 was solved and uploaded by John North
Problem 8 and 9 were solved and uploaded by
Mike Wallace
Problem 6 was solved and uploaded by William Knapper











![{\displaystyle R_{c}=\left[\lim _{k\to \infty }\left|{\frac {(k+2)(k+1)}{(k+1)k}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {k+2}{k}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {1}{1}}\right|\right]^{-1}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d89ec676f3cf615faaeb0997172dcb95b74783ba)


![{\displaystyle R_{c}=\lim _{k\to \infty }\left[{\sqrt[{k}]{\left|{\frac {(-1)^{k}}{\gamma ^{k}}}\right|}}\right]^{-1}=\lim _{k\to \infty }{\frac {{\sqrt[{k}]{|\gamma ^{k}}}|}{\sqrt[{k}]{|(-1)^{k}|}}}=\lim _{k\to \infty }{\frac {\sqrt {|\gamma |}}{\sqrt {|-1|}}}={\sqrt {|\gamma |}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf4cb5edaa63bfb91ef61971c7b7d8f627d672ad)


![{\displaystyle R_{c}=\left[\lim _{k\to \infty }\left|{\frac {\frac {(-1)^{k+1}}{(2(k+1)+1)!}}{\frac {(-1)^{k}}{(2k+1)!}}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {-1}{(2k+3)(2k+2)}}\right|\right]^{-1}=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b721fc0efcd52911cf42fc70932fb7c8ddeaf4d9)


![{\displaystyle R_{c}=\left[\lim _{k\to \infty }\left|{\frac {\frac {(-1)^{k+1}}{(k+2)}}{\frac {(-1)^{k}}{(k+1)}}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {(-1)(k+1)}{(k+2)}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {-1}{1}}\right|\right]^{-1}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cd4a14cdb511abf7e3c8034eb8ea2b23678a9e9)


![{\displaystyle R_{c}=\left[\lim _{k\to \infty }\left|{\frac {\frac {(-1)^{k+2}}{(k+1)2^{k+1}}}{\frac {(-1)^{k+1}}{k2^{k}}}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {-1k}{2(k+1)}}\right|\right]^{-1}=\left[\lim _{k\to \infty }\left|{\frac {-1}{2}}\right|\right]^{-1}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6e30324a52fa7ec79718228b79c6a2b784f05b6)






































![{\displaystyle r(x)=a_{0}+\sum _{n=1}^{\infty }[a_{n}cos(nwx)+b_{n}sin(nwx)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/858d13ad529622b5ebcfb7acfaed39dd0e53bec5)



















![{\displaystyle \displaystyle <f,f>={\frac {1}{7}}\int _{0}^{2\pi }cos^{2}(u)du={\frac {1}{7}}[{\frac {u}{2}}+{\frac {1}{4}}sin2u\mathbf {\mid } _{0}^{2\pi }]={\frac {\pi }{7}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/263cce7ecd18acb9ddad438083778f296463e589)

![{\displaystyle \displaystyle <g,g>={\frac {1}{7}}\int _{0}^{2\pi }sin^{2}(u)du={\frac {1}{7}}[{\frac {u}{2}}-{\frac {1}{4}}sin2u\mid _{0}^{2\pi }]={\frac {\pi }{7}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97164633c3a9ffc4faef325b4d92790d7a003655)













![{\displaystyle \displaystyle \lambda _{1,2}={\frac {1}{2}}[-a\pm {\sqrt {a^{2}-4b}}]={\frac {1}{2}}[3\pm 7]=5,-2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32fd38fa7576045718896b24a05d4d968d62122a)
















![{\displaystyle \displaystyle y'_{p}(x)=e^{-2x}(-3Msin(3x)-2Mcos(3x)+3Ncos(3x)-2Nsin(3x))=e^{-2x}[(-3M-2N)sin(3x)+(-2M+3N)cos(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57e59630b7409a345dd5ea03e26e6d0f9b73fb4c)

![{\displaystyle \displaystyle =2e^{-2x}[(12M-5N)sin(3x)+(13M-12N)cos(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d81b8e488e32c288d1f54bd36e45d78239afe306)
![{\displaystyle \displaystyle 2e^{-2x}[(12M-5N)sin(3x)+(13M-12N)cos(3x)]+4[e^{-2x}[(-3M-2Nsin(3x)+(-2M+3N)cos(3x)]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95d75df2a5f12657a53a39da5862f3186f89477b)
![{\displaystyle \displaystyle +13[e^{-2x}[Mcos(3x)+Nsin(3x)]]=2e^{-2x}cos(3x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f6418320a09c5c1ee69e9763e80550a195079ef)
![{\displaystyle \displaystyle e^{-2x}[(24M-10N)sin(3x)+(26M-24N)cos(3x)+(-12M-8N)sin(3x)+(-8M+12N)cos(3x)+13Mcos(3x)+13Nsin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cea19074022c2229385c5047fb58f026dcbb239)





![{\displaystyle \displaystyle y_{p}(x)=e^{-2x}[{\frac {10}{11}}cos(3x)+{\frac {24}{11}}sin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bb9afdf7616bf58cccd80df8b554b97d149bbb1)
![{\displaystyle \displaystyle y_{h}(x)=e^{-2x}[Acos(3x)+Bsin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b76122f69f374297e69cd0733255c40882d7b3)
![{\displaystyle \displaystyle y'_{h}(x)=e^{-2x}(-3Asin(3x)-2Acos(3x)+3Bcos(3x)-2Bsin(3x))=e^{-2x}[(-3A-2B)sin(3x)+(-2A+3B)cos(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e97310806a2ca538f50780255d53f3439bf777a1)
![{\displaystyle \displaystyle y_{h}(0)=e^{-2x}[Acos(3x)+Bsin(3x)]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffc00dbfda6b2c926f9884abe6d7001a1e53b9db)
![{\displaystyle \displaystyle y'_{h}(x)=e^{-2x}[(-3A-2B)sin(3x)+(-2A+3B)cos(3x)]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/619688406e79bb47ca01d1ea36d30112ad8d50c8)


![{\displaystyle \displaystyle y_{h}(x)=e^{-2x}[cos(3x)+{\frac {3}{2}}sin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff17ff2c1c6abd9c59f0c16cd6a120ee0aeb919)
![{\displaystyle \displaystyle y(x)=y_{h}(x)+y_{p}(x)=e^{-2x}[cos(3x)+{\frac {3}{2}}sin(3x)]+e^{-2x}[{\frac {10}{11}}cos(3x)+{\frac {24}{11}}sin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ecacb10a8174f4c79a42670677353930f528306)
![{\displaystyle \displaystyle y(x)=e^{-2x}[{\frac {21}{11}}cos(3x)+{\frac {81}{22}}sin(3x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/254db9075f5b197df5ac99cca8b1d36b5819af19)

































![{\displaystyle \ \int x^{0}log(1+x)dx=log(1+x)[x+1]-x\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f3609807f317cef95c4cdcd1d0d90d3896fdb7a)
![{\displaystyle \ \int x^{1}log(1+x)dx={\frac {1}{2}}*[(x-log(1+x))+x^{2}log(1+x)-{\frac {x^{2}}{2}}]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e372b7cb59ec182b8614199a2e07058daa0bf49)



![{\displaystyle \ [b_{j}(x)=x^{j},j=0,1,...,n]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dc72c6a0e4fd696b1058039ce8110ad77653a7a)


![{\displaystyle \ [-{\frac {3}{4}},3],\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb66d40d4df2c944438f22654e25df8b28a2adeb)



![{\displaystyle \ [-{\frac {3}{4}},3].\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/688918f3fdad89b20488740db39ba67f3bdfc4a6)
























