Report 2
Given the two roots and the initial conditions:
|

|
(1.0)
|
|

|
(1.1)
|
Part 1.
Find the non-homogeneous L2-ODE-CC in standard form. Find the solution in terms of the initial conditions and the general excitation 
Now with no excitation and plot the solution:
|

|
(1.2)
|
Part 2.
Generate 3 non-standard (and non-homogeneous) L2-ODE-CC that admit the two values  as the two roots of the corresponding characteristic equation.
as the two roots of the corresponding characteristic equation.
Part 1.
Characteristic Equation:
|

|
(1.3)
|
|

|
(1.4)
|
|

|
(1.5)
|
Non-Homogeneous L2-ODE-CC:
|

|
(1.6)
|
Homogenous Solution:
|

|
(1.7)
|
Overall Solution:
|

|
(1.8)
|
|

|
(1.9)
|
Satisfy Initial Conditions:
|

|
(1.10)
|
|

|
(1.11)
|
No excitation:
|

|
(1.12)
|
From (1.10):
|

|
(1.13)
|
From (1.11):
|

|
(1.14)
|
|

|
(1.15)
|
|

|
(1.16)
|
Plug (1.13) into (1.16):
|

|
(1.17)
|
Solve for  :
:
|

|
(1.18)
|
Plug (1.18) into (1.13) and solve for  :
:
|

|
(1.19)
|
Therefore, the final solution in terms of the initial conditions and the general excitation  is:
is:
|

|
(1.20)
|
Plot of Solution:
Figure 1
Part 2.
Three non-standard and non-homogeneous solutions using the same roots given above:
1.
|

|
(1.21)
|
|

|
(1.22)
|
2.
|

|
(1.23)
|
|

|
(1.24)
|
3.
|

|
(1.25)
|
|

|
(1.26)
|
This problem was solved and uploaded by [Derik Bell]
This problem was proofread by: David Herrick
From Section 5 in the notes, pg. 5-6
Solve the L2-ODE-CC from pg. 5-5, equation (4)

For initial conditions:

Where there is no excitation, i.e. 

Factoring:

Thus, there is a double root, where 
Because there is no excitation, the homogenous solution will be the same as the final solution. Thus, the solution will be:

Plugging in the initial condition,


In order to solve for the second constant, we need to take a derivative.

Plugging in C1 and the other initial condition:


So, the final solution is:

Matlab Code:
x = 0:0.001:1;
f = exp(5*x) - 5*x.*exp(5*x);
plot(x,f)
xlabel ('x')
ylabel ('y(x)')

This problem was solved and uploaded by [David Herrick]
This problem was checked by [William Knapper]
Complete problems 3 and 4 from p.59 of K 2011.
The two problems have the same instructions: "Find a general solution. Check your answer by substitution."

We start by using the characteristic equation of this ODE in order to find the roots. We use:

where a = 6 and b = 8.96. Taking the discriminant, we find that

A positive discriminant implies that there exists two real roots, with a general solution of the form:

To find the unknowns, we find the roots of the above equation:


Therefore, the correct general solution is:

To check that this solution is correct, we take the first and second derivatives:


Now, we plug these values into the original equation:

Upon further inspection, all the terms on the left side of the equation cancel out and equal zero.

We start by using the characteristic equation of this ODE in order to find the roots. We use:

where a = 4 and b = (π^2 + 4). Taking the discriminant, we find that

A negative discriminant implies that there exists complex conjugate roots to this equation. The general solution for this type of equation is

Where

This yields

To verify that this is the correct solution, we first find the first and second derivatives of the solution:


![{\displaystyle \displaystyle {y}''=e^{-2x}[-A\pi ^{2}cos(\pi x)-B\pi ^{2}sin(\pi x)+2A\pi sin(\pi x)-2B\pi sin(\pi x)]-2e^{-2x}[-A\pi sin(\pi x)+B\pi cos(\pi x)-2Acos(\pi x)-2Bsin(\pi x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8300d555eb4b34f7134144d24d2baf6d4dc93765)
We then plug these values into the original problem to get this somewhat lengthy equation:



Upon further inspection, all the terms on the left side of the equation cancel out to 0.
This problem was solved and uploaded by: (Will Knapper)
This problem was proofread by: David Herrick
K 2011 p.59 pbs.5,6.
Find a general solution. Check your answer by substitution.

Determine the characteristic equation and the nature of the determinate:



Characteristic Equation:


0 indicates a real double root, therefore:

 from the original equation. Therefore:
from the original equation. Therefore:



Substituting into the original equation gives:
![{\displaystyle e^{-\pi x}[(C_{1}\pi ^{2}+C_{2}\pi ^{2}x-2C_{2}\pi )+2\pi (C_{2}-\pi C_{1}-\pi C_{2}x)+\pi ^{2}(C_{1}+C_{2}x)]=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/aada377570b5bf449c757f5f60d74b8583da05c1)
![{\displaystyle =e^{-\pi x}[C_{1}\pi ^{2}+C_{2}\pi ^{2}x-2C_{2}\pi +2C_{2}\pi -2C_{1}\pi ^{2}-2C_{2}\pi ^{2}x+C_{1}\pi ^{2}+C_{2}\pi ^{2}x]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/45bc613a9b93d33de3f4ac09806afc62f4ef7fc6)
Canceling gives 0 = 0, confirming the general solution found above.
This problem was solved and uploaded by: (John North)
This problem was proofread by: David Herrick

Reduce original equation so that the first coefficient is 1:

Determine the characteristic equation and the nature of the determinate:



Characteristic Equation:


0 indicates a real double root, therefore:

 from the original equation. Therefore:
from the original equation. Therefore:



Substituting into the original equation gives:
![{\displaystyle e^{1.6x}[(2.56C_{1}+2.56C_{2}x+3.2C_{2})-3.2(1.6C_{1}+1.6C_{2}x+C_{2})+2.56(C_{1}+C_{2}x)]=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/323dec43006002a120ca64e18013747aa3910111)
![{\displaystyle =e^{1.6x}[(2.56C_{1}+2.56C_{2}x+3.2C_{2}-5.12C_{1}-5.12C_{2}x-3.2C_{2}+2.56C_{1}+2.56C_{2}x]=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/69e78b0c6b060d61fb5b21b5d05b2c614f478944)
Canceling gives 0 = 0, confirming that general solution found above.
This problem was solved and uploaded by: (John North)
This problem was proofread by: David Herrick
Problems 16 and 17 from pg. 59 of the textbook. The two questions have the same instructions: Find an ODE of the form

for the given basis.

This basis implies that there are two distinct, real roots: 2.6 and -4.3. We put these roots into the characteristic equation to get:

Then, you convert the characteristic equation to a regular ODE:


A basis of this form implies that the solution is of the form:

The real double root can be found by this equation:

That means that the characteristic equation can be found by solving:

Converting the characteristic equation to the ODE, we get:

This problem was solved and uploaded by: (Will Knapper)
This problem was proofread by (Josh House)
Realize spring-dashpot-mass system in series as shown in Fig. p.1-4 with the similar characteristic as in (3)p.5-5, but with the double real root  , i.e., find values for parameters k,c,m.
, i.e., find values for parameters k,c,m.
First we put the double root into the characteristic equation:


The corresponding L2-ODE is:

The equation of motion of the spring-dashpot-mass system is:
 [1]
[1]
or:

Solving for the parameters k,c,m:



We get:



This problem was solved and uploaded by: (Radina Dikova)
This problem was proofread by: Mike Wallace
Develop the McLauren series (Taylor series at t=0) for e^t, cos(t), and sin(t).
The general form of the Taylor series expansion at point a is

for  at t=0:
at t=0:


for  at t=0:
at t=0:


for  at t=0:
at t=0:


This problem was solved and uploaded by: (John North)
This problem was checked by: William Knapper
Find a general solution. Check your answer by substitution.
8. 
15. 
8. 
Writing the characteristic equation:

Which is now in the form:

Solving for the two roots:

We will find the discriminant to be less than 0, leading to complex conjugate roots:

Which leads to a solution of the form:

Where  , therefore:
, therefore:

Giving us a solution of:

Checking our solution:



Plugging all of this into the original differential equation and combining like terms gives us:
![{\displaystyle \displaystyle [{\frac {1}{4}}-3-{\frac {1}{2}}+3.25]e^{-x/2}Acos({\sqrt {3}}x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b69f0412c24e4491a9b00c1298686214a833cf4)
![{\displaystyle \displaystyle [{\frac {\sqrt {3}}{2}}+{\frac {\sqrt {3}}{2}}-{\sqrt {3}}]e^{-x/2}Asin({\sqrt {3}}x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc97121031773db368b895d256025e57d020aa0c)
![{\displaystyle \displaystyle [-{\frac {\sqrt {3}}{2}}-{\frac {\sqrt {3}}{2}}+{\sqrt {3}}]e^{-x/2}Bcos({\sqrt {3}}x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/796743f555f6cf2a29bb30469e3622456e67b965)
![{\displaystyle \displaystyle [{\frac {1}{4}}-3-{\frac {1}{2}}+3.25]e^{-x/2}Bsin({\sqrt {3}}x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/808da5682351b40de7ec5386a0ba2841c9bd3a6c)
The terms in the brackets all add up to zero, thus verifying we have a correct solution to our problem.
15. 
Writing the characteristic equation:

Which is now in the form:

Solving for the two roots:

We will find the discriminant to be less than 0, leading to complex conjugate roots:

Which leads to a solution of the form:

Where  , therefore:
, therefore:

Giving us a solution of:

Checking our solution:



Plugging all of this into the original differential equation and combining like terms gives us:
![{\displaystyle \displaystyle [0.0729-\pi -0.1458+0.0729+\pi ]e^{-0.27x}Acos{\sqrt {\pi }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e423efb4ce1653471cde7f4348a478da1adf322b)
![{\displaystyle \displaystyle [0.27{\sqrt {\pi }}+0.27{\sqrt {\pi }}-0.54{\sqrt {\pi }}]e^{-0.27x}Asin{\sqrt {\pi }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/758869ed884e017d53814da69f890d364940ecad)
![{\displaystyle \displaystyle [-0.27{\sqrt {\pi }}-0.27{\sqrt {\pi }}+0.54{\sqrt {\pi }}]e^{-0.27x}Bcos{\sqrt {\pi }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c3e681158c55210637c1ab5e1447517ed241e77)
![{\displaystyle \displaystyle [0.0729-\pi -0.1458+0.0729+\pi ]e^{-0.27x}Bsin{\sqrt {\pi }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7cc3ee5fd346a4608ef70debce5f61fd3ff6e65)
The terms in the brackets all add up to zero, thus verifying we have a correct solution to our problem.
This problem was solved and uploaded by: (Josh House)
This problem was proofread by: (Radina Dikova)
For the given ODE, find and plot the solution for the L2-ODE-CC corresponding to

In another figure superpose this figure, Fig. from R2.6 p.5-6, and the Fig. from R2-1 p.3-7.
This corresponds to the L2-ODE-CC in standard form

Initial conditions

Where there is no excitation

Solving the quadratic equation for  determines the roots of the ODE
determines the roots of the ODE


The roots of the quadratic equation come out to be:

The general homogeneous solution of the ODE will resemble the following form.

Plugging in the roots into the equation we get

Implementing initial conditions where: 



So from our initial conditions the constants are determined to be

The final solution becomes


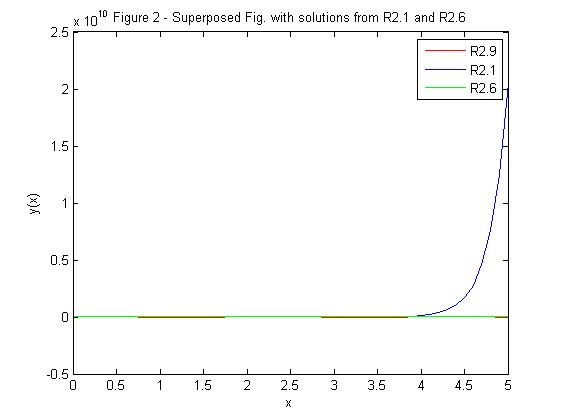
This problem was solved and uploaded by: Mike Wallace
This problem was proofread by John North
Problem 2 was solved and Problems 1, 3, and 4 were proofread by David Herrick 15:56, 6 February 2012 (UTC)
Problem 8 was solved and Problem 5 was proofread by Josh House 23:41, 7 February 2012 (UTC)
Problem 6 was solved and Problem 8 was proofread by Radina Dikova 16:26, 7 February 2012 (UTC)
Problem 9 was solved and Problem 6 was proofread by Mike Wallace 23:35, 7 February 2012 (UTC)
Problems 3 and 5 were solved and Problems 2 and 7 were proofread by William Knapper 05:04, 8 February 2012 (UTC)
Problem 1 was solved by Derik Bell 15:44, 8 February 2012 (UTC)
Problems 4 and 7 were solved and Problem 9 was proofread by John North 15:47, 8 February 2012 (UTC)
- ↑ Vu-Quoc
, Loc. 2012. IEA S12 Lecture notes, audios, videos. Section 1(d) https://docs.google.com/Doc?id=dc82nfgb_858gmw855hj
































































![{\displaystyle \displaystyle {y}''=e^{-2x}[-A\pi ^{2}cos(\pi x)-B\pi ^{2}sin(\pi x)+2A\pi sin(\pi x)-2B\pi sin(\pi x)]-2e^{-2x}[-A\pi sin(\pi x)+B\pi cos(\pi x)-2Acos(\pi x)-2Bsin(\pi x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8300d555eb4b34f7134144d24d2baf6d4dc93765)














![{\displaystyle e^{-\pi x}[(C_{1}\pi ^{2}+C_{2}\pi ^{2}x-2C_{2}\pi )+2\pi (C_{2}-\pi C_{1}-\pi C_{2}x)+\pi ^{2}(C_{1}+C_{2}x)]=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/aada377570b5bf449c757f5f60d74b8583da05c1)
![{\displaystyle =e^{-\pi x}[C_{1}\pi ^{2}+C_{2}\pi ^{2}x-2C_{2}\pi +2C_{2}\pi -2C_{1}\pi ^{2}-2C_{2}\pi ^{2}x+C_{1}\pi ^{2}+C_{2}\pi ^{2}x]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/45bc613a9b93d33de3f4ac09806afc62f4ef7fc6)








![{\displaystyle e^{1.6x}[(2.56C_{1}+2.56C_{2}x+3.2C_{2})-3.2(1.6C_{1}+1.6C_{2}x+C_{2})+2.56(C_{1}+C_{2}x)]=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/323dec43006002a120ca64e18013747aa3910111)
![{\displaystyle =e^{1.6x}[(2.56C_{1}+2.56C_{2}x+3.2C_{2}-5.12C_{1}-5.12C_{2}x-3.2C_{2}+2.56C_{1}+2.56C_{2}x]=0\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/69e78b0c6b060d61fb5b21b5d05b2c614f478944)








































![{\displaystyle \displaystyle [{\frac {1}{4}}-3-{\frac {1}{2}}+3.25]e^{-x/2}Acos({\sqrt {3}}x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b69f0412c24e4491a9b00c1298686214a833cf4)
![{\displaystyle \displaystyle [{\frac {\sqrt {3}}{2}}+{\frac {\sqrt {3}}{2}}-{\sqrt {3}}]e^{-x/2}Asin({\sqrt {3}}x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc97121031773db368b895d256025e57d020aa0c)
![{\displaystyle \displaystyle [-{\frac {\sqrt {3}}{2}}-{\frac {\sqrt {3}}{2}}+{\sqrt {3}}]e^{-x/2}Bcos({\sqrt {3}}x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/796743f555f6cf2a29bb30469e3622456e67b965)
![{\displaystyle \displaystyle [{\frac {1}{4}}-3-{\frac {1}{2}}+3.25]e^{-x/2}Bsin({\sqrt {3}}x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/808da5682351b40de7ec5386a0ba2841c9bd3a6c)







![{\displaystyle \displaystyle [0.0729-\pi -0.1458+0.0729+\pi ]e^{-0.27x}Acos{\sqrt {\pi }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e423efb4ce1653471cde7f4348a478da1adf322b)
![{\displaystyle \displaystyle [0.27{\sqrt {\pi }}+0.27{\sqrt {\pi }}-0.54{\sqrt {\pi }}]e^{-0.27x}Asin{\sqrt {\pi }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/758869ed884e017d53814da69f890d364940ecad)
![{\displaystyle \displaystyle [-0.27{\sqrt {\pi }}-0.27{\sqrt {\pi }}+0.54{\sqrt {\pi }}]e^{-0.27x}Bcos{\sqrt {\pi }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c3e681158c55210637c1ab5e1447517ed241e77)
![{\displaystyle \displaystyle [0.0729-\pi -0.1458+0.0729+\pi ]e^{-0.27x}Bsin{\sqrt {\pi }}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7cc3ee5fd346a4608ef70debce5f61fd3ff6e65)














