<Team 15
REPORT 2
λ
1
=
−
2
{\displaystyle \lambda _{1}=-2\!}
λ
2
=
+
5
{\displaystyle \lambda _{2}=+5\!}
y
(
0
)
=
1
{\displaystyle y(0)=1\!}
y
′
(
0
)
=
0
{\displaystyle y{}'(0)=0\!}
r
(
x
)
=
0
{\displaystyle r(x)=0\!}
Find the non-homogeneous linear 2nd order ordinary differential equation with constant coefficients in standard form and the solution in terms of the initial conditions and the general excitation
r
(
x
)
{\displaystyle r(x)}
Then plot the solution.
Some of the following standard equations were referenced from the textbook Advanced Engineering Mechanics 10th Ed. Kreyszig 2011.
Standard Form:
λ
2
+
a
λ
+
b
=
0
{\displaystyle \lambda ^{2}+a\lambda +b=0\!}
(
λ
−
λ
1
)
(
λ
−
λ
2
)
=
0
{\displaystyle (\lambda -\lambda _{1})(\lambda -\lambda _{2})=0\!}
λ
2
−
λ
λ
2
−
λ
λ
1
+
λ
1
λ
2
=
0
{\displaystyle \lambda ^{2}-\lambda \lambda _{2}-\lambda \lambda _{1}+\lambda _{1}\lambda _{2}=0\!}
λ
2
−
5
λ
+
2
λ
−
10
=
0
{\displaystyle \lambda ^{2}-5\lambda +2\lambda -10=0\!}
λ
2
−
3
λ
−
10
=
0
{\displaystyle \lambda ^{2}-3\lambda -10=0\!}
a
=
−
3
{\displaystyle a=-3\!}
b
=
−
10
{\displaystyle b=-10\!}
y
″
+
a
y
′
+
b
y
=
r
(
x
)
=
0
{\displaystyle y{}''+ay{}'+by=r(x)=0\!}
y
″
−
3
y
′
−
10
y
=
0
{\displaystyle y{}''-3y{}'-10y=0\!}
y
(
x
)
=
y
h
(
x
)
+
y
p
(
x
)
{\displaystyle y(x)=y_{h}(x)+y_{p}(x)\!}
y
h
(
x
)
=
c
1
e
−
2
x
+
c
2
e
5
x
{\displaystyle y_{h}(x)=c_{1}e^{-2x}+c_{2}e^{5x}\!}
y
p
(
x
)
=
0
{\displaystyle y_{p}(x)=0\!}
Therefore,
y
p
′
(
x
)
=
0
{\displaystyle y_{p}{}'(x)=0\!}
y
(
x
)
=
c
1
e
−
2
x
+
c
2
e
5
x
{\displaystyle y(x)=c_{1}e^{-2x}+c_{2}e^{5x}\!}
y
′
(
x
)
=
−
2
c
1
e
−
2
x
+
5
c
2
e
5
x
{\displaystyle y{}'(x)=-2c_{1}e^{-2x}+5c_{2}e^{5x}\!}
If
y
(
0
)
=
1
{\displaystyle y(0)=1\!}
then
1
=
c
1
e
−
2
(
0
)
+
c
2
e
5
(
0
)
{\displaystyle 1=c_{1}e^{-2(0)}+c_{2}e^{5(0)}\!}
1
=
c
1
+
c
2
{\displaystyle 1=c_{1}+c_{2}\!}
If
y
′
(
0
)
=
0
{\displaystyle y{}'(0)=0\!}
then
0
=
c
1
e
−
2
(
0
)
+
c
2
e
5
(
0
)
{\displaystyle 0=c_{1}e^{-2(0)}+c_{2}e^{5(0)}\!}
0
=
c
1
+
c
2
{\displaystyle 0=c_{1}+c_{2}\!}
2
c
1
=
5
c
2
{\displaystyle 2c_{1}=5c_{2}\!}
c
1
=
5
2
c
2
{\displaystyle c_{1}={\frac {5}{2}}c_{2}\!}
1
=
5
2
c
2
+
c
2
{\displaystyle 1={\frac {5}{2}}c_{2}+c_{2}\!}
1
=
7
2
c
2
{\displaystyle 1={\frac {7}{2}}c_{2}\!}
c
2
=
2
7
{\displaystyle c_{2}={\frac {2}{7}}\!}
1
=
c
1
+
c
2
{\displaystyle 1=c_{1}+c_{2}\!}
c
1
=
1
−
c
2
=
1
−
2
7
=
5
7
{\displaystyle c_{1}=1-c_{2}=1-{\frac {2}{7}}={\frac {5}{7}}\!}
Final Solution:
y
(
x
)
=
5
7
e
−
2
x
+
2
7
e
5
x
{\displaystyle y(x)={\frac {5}{7}}e^{-2x}+{\frac {2}{7}}e^{5x}\!}
Solved and typed by Kristin Howe
Solved and typed by -
Problems referenced from Advanced Engineering Mechanics 10th Ed. Kreyszig 2011 p.59 problems.3-4
3a)
y
″
+
6
y
′
+
8.96
y
=
0
{\displaystyle y{}''+6{}y'+8.96y=0\!}
3b)
y
″
+
4
y
′
+
(
π
2
+
4
)
y
=
0
{\displaystyle y''+4y'+(\pi ^{2}+4)y=0\!}
Find the general solution of the ODEs.
3a)
y
″
+
6
y
′
+
8.96
y
=
0
{\displaystyle y{}''+6{}y'+8.96y=0\!}
a
=
6
{\displaystyle a=6\!}
b
=
8.96
{\displaystyle b=8.96\!}
λ
2
+
a
λ
+
b
=
0
{\displaystyle \lambda ^{2}+a\lambda +b=0\!}
λ
2
+
6
λ
+
8.96
=
0
{\displaystyle \lambda ^{2}+6\lambda +8.96=0\!}
Using the quadratic formula:
λ
1
/
2
=
−
b
±
b
2
−
4
a
c
2
{\displaystyle \lambda _{1/2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2}}\,\!}
λ
1
/
2
,
{\displaystyle \lambda _{1/2},\!}
Plug-in and solve using known variables (b=6, a=1, c=8.96)
λ
1
/
2
=
−
6
±
0.16
2
{\displaystyle \lambda _{1/2}={\frac {-6\pm {\sqrt {0.16}}}{2}}\,\!}
=
−
6
±
0.4
2
{\displaystyle ={\frac {-6\pm 0.4}{2}}\,\!}
=
−
3
±
0.2
{\displaystyle =-3\pm 0.2\,\!}
Therefore,
λ
1
=
−
2.8
{\displaystyle \lambda _{1}=-2.8\,\!}
λ
2
=
−
3.2
{\displaystyle \lambda _{2}=-3.2\,\!}
The General Solution formula for Distinct Real roots is
y
(
x
)
=
C
1
e
λ
1
x
+
C
2
e
λ
2
x
{\displaystyle y(x)=C_{1}e^{\lambda _{1}x}+C_{2}e^{\lambda _{2}x}}
Now substitute the known roots into the General Solution formula:
y
(
x
)
=
C
1
e
−
2.8
x
+
C
2
e
−
3.2
x
{\displaystyle y(x)=C_{1}e^{-2.8x}+C_{2}e^{-3.2x}\!}
Check using substitution. First, find the 1st and 2nd derivative of general solution formula:
y
′
=
−
3.2
C
1
e
−
3.2
x
−
2.8
C
2
e
−
2.8
x
{\displaystyle {y}'=-3.2C_{1}e^{-3.2x}-2.8C_{2}e^{-2.8x}\!}
y
″
=
10.24
C
1
e
−
3.2
x
+
7.84
C
2
e
−
2.8
x
{\displaystyle {y}''=10.24C_{1}e^{-3.2x}+7.84C_{2}e^{-2.8x}\!}
Then, plug in the known variables into the original equation:
y
″
+
6
y
′
+
8.96
y
=
0
{\displaystyle y{}''+6{}y'+8.96y=0\!}
10.24
c
1
e
−
3.2
x
+
7.84
c
2
e
−
2.8
x
−
19.2
c
1
e
−
3.2
x
−
16.8
c
2
e
−
2.8
x
+
8.96
c
1
e
−
3.2
x
+
8.96
c
2
e
−
2.8
x
=
0
{\displaystyle 10.24c_{1}e^{-3.2x}+7.84c_{2}e^{-2.8x}-19.2c_{1}e^{-3.2x}-16.8c_{2}e^{-2.8x}+8.96c_{1}e^{-3.2x}+8.96c_{2}e^{-2.8x}=0\!}
By inspection, all of the terms on the left side of the equation cancel out to 0, making the expression correct.
Therefore, the general solution is correct.
3b)
y
″
+
4
y
′
+
(
π
2
+
4
)
y
=
0
{\displaystyle y''+4y'+(\pi ^{2}+4)y=0\!}
a
=
4
{\displaystyle a=4\!}
b
=
(
π
2
+
4
)
{\displaystyle b=(\pi ^{2}+4)\!}
λ
2
+
a
λ
+
b
=
0
{\displaystyle \lambda ^{2}+a\lambda +b=0\!}
λ
2
+
4
λ
+
(
π
2
+
4
)
=
0
{\displaystyle \lambda ^{2}+4\lambda +(\pi ^{2}+4)=0\!}
Using the quadratic formula:
λ
1
/
2
=
−
b
±
b
2
−
4
a
c
2
{\displaystyle \lambda _{1/2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2}}\,\!}
λ
1
/
2
,
{\displaystyle \lambda _{1/2},\!}
Plug-in and solve using known variables (b=4, a=1, c=[
π
2
{\displaystyle \pi ^{2}}
λ
1
/
2
=
−
4
±
−
4
π
2
2
{\displaystyle \lambda _{1/2}={\frac {-4\pm {\sqrt {-4\pi ^{2}}}}{2}}\,\!}
=
−
4
±
2
π
i
2
{\displaystyle ={\frac {-4\pm 2\pi i}{2}}\,\!}
=
−
2
±
π
i
{\displaystyle =-2\pm \pi i\,\!}
Therefore,
λ
1
=
−
2
+
π
i
{\displaystyle \lambda _{1}=-2+\pi i\,\!}
λ
2
=
−
2
−
π
i
{\displaystyle \lambda _{2}=-2-\pi i\,\!}
The General Solution formula for Complex Conjugate roots is
y
(
x
)
=
e
−
α
x
2
(
C
1
cos
β
x
+
C
2
sin
β
x
)
{\displaystyle y(x)=e^{-{\frac {\alpha x}{2}}}(C_{1}\cos \beta x+C_{2}\sin \beta x)\!}
Now substitute the known roots into the General Solution formula:
y
(
x
)
=
e
−
2
x
(
C
1
cos
π
x
+
C
2
sin
π
x
)
{\displaystyle y(x)=e^{-2x}(C_{1}\cos \pi x+C_{2}\sin \pi x)\!}
Check using substitution. First, find the 1st and 2nd derivative of general solution formula:
y
′
=
e
−
2
x
(
−
C
1
π
s
i
n
(
π
x
)
+
C
2
π
c
o
s
(
π
x
)
)
−
2
e
−
2
x
(
C
1
c
o
s
(
π
x
)
+
C
2
s
i
n
(
π
x
)
)
{\displaystyle {y}'=e^{-2x}(-C_{1}\pi sin(\pi x)+C_{2}\pi cos(\pi x))-2e^{-2x}(C_{1}cos(\pi x)+C_{2}sin(\pi x))\!}
y
″
=
e
−
2
x
(
−
C
1
π
2
c
o
s
(
π
x
)
−
C
2
π
2
s
i
n
(
π
x
)
+
2
C
1
π
s
i
n
(
π
x
)
−
2
C
2
π
s
i
n
(
π
x
)
)
−
2
e
−
2
x
(
−
C
1
π
s
i
n
(
π
x
)
+
C
2
π
c
o
s
(
π
x
)
−
2
C
1
c
o
s
(
π
x
)
−
2
C
2
s
i
n
(
π
x
)
)
{\displaystyle {y}''=e^{-2x}(-C_{1}\pi ^{2}cos(\pi x)-C_{2}\pi ^{2}sin(\pi x)+2C_{1}\pi sin(\pi x)-2C_{2}\pi sin(\pi x))-2e^{-2x}(-C_{1}\pi sin(\pi x)+C_{2}\pi cos(\pi x)-2C_{1}cos(\pi x)-2C_{2}sin(\pi x))\!}
y
″
+
4
y
′
+
(
π
2
+
4
)
y
=
0
{\displaystyle y''+4y'+(\pi ^{2}+4)y=0\!}
e
−
2
x
(
−
C
1
π
2
c
o
s
(
π
x
)
−
C
2
π
2
s
i
n
(
π
x
)
+
2
C
1
π
s
i
n
(
π
x
)
−
2
C
2
π
s
i
n
(
π
x
)
)
−
2
e
−
2
x
(
−
C
1
π
s
i
n
(
π
x
)
+
C
2
π
c
o
s
(
π
x
)
−
2
C
1
c
o
s
(
π
x
)
−
2
C
2
s
i
n
(
π
x
)
)
{\displaystyle e^{-2x}(-C_{1}\pi ^{2}cos(\pi x)-C_{2}\pi ^{2}sin(\pi x)+2C_{1}\pi sin(\pi x)-2C_{2}\pi sin(\pi x))-2e^{-2x}(-C_{1}\pi sin(\pi x)+C_{2}\pi cos(\pi x)-2C_{1}cos(\pi x)-2C_{2}sin(\pi x))\!}
+
4
(
e
−
2
x
(
−
C
1
π
s
i
n
(
π
x
)
+
C
2
π
c
o
s
(
π
x
)
)
−
2
e
−
2
x
(
C
1
c
o
s
(
π
x
)
+
C
2
s
i
n
(
π
x
)
)
)
{\displaystyle +4(e^{-2x}(-C_{1}\pi sin(\pi x)+C_{2}\pi cos(\pi x))-2e^{-2x}(C_{1}cos(\pi x)+C_{2}sin(\pi x)))\!}
+
(
π
2
+
4
)
(
e
−
2
x
(
C
1
cos
π
x
+
C
2
sin
π
x
)
)
=
0
{\displaystyle +(\pi ^{2}+4)(e^{-2x}(C_{1}\cos \pi x+C_{2}\sin \pi x))=0\!}
By inspection, all of the terms on the left side of the equation cancel out to 0, making the expression correct.
Therefore, the general solution is correct.
Solved and typed by - Tim Pham 19:36, 07 February 2012 (UTC)
The following problems are referenced from Advanced Engineering Mechanics 10th Ed. Kreyszig 2011 p.59.
For additional information and/or practice reference Advanced Engineering Mechanics 10th Ed. Kreyszig 2011 p.53-59 and the
lecture notes Lecture 5 .
Note the lecture notes and Advanced Engineering Mechanics 10th Ed. Kreyszig 2011 textbook were used to solve the following. 4a)
y
″
+
2
π
y
′
+
π
2
y
=
0
{\displaystyle y{}''+2\pi {}y'+\pi ^{2}y=0\!}
4b)
10
y
″
−
32
y
′
+
25.6
y
=
0
{\displaystyle 10y{}''-32{}y'+25.6{}y=0\!}
Find the general solution. Check answer by substitution.
4a)
y
″
+
2
π
y
′
+
π
2
y
=
0
{\displaystyle y{}''+2\pi {}y'+\pi ^{2}y=0\!}
a
=
2
π
{\displaystyle a=2\pi \!}
b
=
π
2
{\displaystyle b=\pi ^{2}\!}
λ
2
+
a
λ
+
b
=
0
{\displaystyle \lambda ^{2}+a\lambda +b=0\!}
λ
2
+
2
π
λ
+
π
2
=
0
{\displaystyle \lambda ^{2}+2\pi \lambda +\pi ^{2}=0\!}
Finding the roots:
λ
1
=
1
2
(
−
2
π
+
(
−
2
π
)
2
−
4
(
π
2
)
)
=
−
π
{\displaystyle \lambda _{1}={\frac {1}{2}}(-2\pi +{\sqrt {(-2\pi )^{2}-4(\pi ^{2})}})=-\pi \!}
λ
2
=
1
2
(
−
2
π
−
(
−
2
π
)
2
−
4
(
π
2
)
)
=
−
π
{\displaystyle \lambda _{2}={\frac {1}{2}}(-2\pi -{\sqrt {(-2\pi )^{2}-4(\pi ^{2})}})=-\pi \!}
y
1
=
e
−
π
x
{\displaystyle y_{1}=e^{-\pi {x}}\!}
y
2
=
u
y
1
{\displaystyle y_{2}=uy_{1}\!}
u
=
c
1
x
+
c
2
{\displaystyle u=c_{1}x+c_{2}\!}
So,
y
2
=
(
c
1
x
+
c
2
)
y
1
{\displaystyle y_{2}=(c_{1}x+c_{2})y_{1}\!}
c
1
=
1
c
2
=
0
{\displaystyle c_{1}=1c_{2}=0\!}
y
2
=
(
x
+
0
)
y
1
{\displaystyle y_{2}=(x+0)y_{1}\!}
y
2
=
x
y
1
{\displaystyle y_{2}=xy_{1}\!}
y
2
=
x
e
−
π
x
{\displaystyle y_{2}=xe^{-\pi {x}}\!}
y
=
(
c
1
+
c
2
x
)
e
−
π
x
{\displaystyle y=(c_{1}+c_{2}x)e^{-\pi {x}}\!}
General Solution
Check by substitution
y
=
(
c
1
+
c
2
x
)
e
−
π
x
{\displaystyle y=(c_{1}+c_{2}x)e^{-\pi {x}}\!}
y
′
=
−
π
c
1
e
−
π
x
+
c
2
e
−
π
x
−
π
c
2
e
−
π
x
{\displaystyle y'=-\pi {}c_{1}e^{-\pi {x}}+c_{2}e^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}\!}
y
″
=
π
2
c
1
e
−
π
x
−
π
c
2
e
−
π
x
+
π
2
c
2
x
e
−
π
x
−
π
c
2
e
−
π
x
{\displaystyle y''=\pi ^{2}c_{1}e^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}+\pi ^{2}c_{2}xe^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}\!}
π
2
c
1
e
−
π
x
−
π
c
2
e
−
π
x
+
π
2
c
2
x
e
−
π
x
−
π
c
2
e
−
π
x
+
2
π
(
−
π
c
1
e
−
π
x
+
c
2
e
−
π
x
−
π
c
2
e
−
π
x
)
+
π
2
(
e
−
π
x
c
1
+
e
−
π
x
x
c
2
)
=
0
{\displaystyle \pi ^{2}c_{1}e^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}+\pi ^{2}c_{2}xe^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}}+2\pi {}(-\pi {}c_{1}e^{-\pi {x}}+c_{2}e^{-\pi {x}}-\pi {}c_{2}e^{-\pi {x}})+\pi ^{2}(e^{-\pi {x}}c_{1}+e^{-\pi {x}}xc_{2})=0\!}
y
=
(
c
1
+
c
2
x
)
e
−
π
x
{\displaystyle y=(c_{1}+c_{2}x)e^{-\pi {x}}\!}
4b)
10
y
″
−
32
y
′
+
25.6
y
=
0
{\displaystyle 10y{}''-32{}y'+25.6{}y=0\!}
y
″
−
3.2
y
′
+
2.56
y
=
0
{\displaystyle y{}''-3.2{}y'+2.56{}y=0\!}
a
=
−
3.2
{\displaystyle a=-3.2\!}
b
=
2.56
{\displaystyle b=2.56\!}
λ
2
+
a
λ
+
b
=
0
{\displaystyle \lambda ^{2}+a\lambda +b=0\!}
λ
2
−
3.2
λ
+
2.56
=
0
{\displaystyle \lambda ^{2}-3.2\lambda +2.56=0\!}
λ
1
=
1
2
(
−
(
−
3.2
)
+
(
−
3.2
)
2
−
4
(
2.56
)
)
=
1.6
{\displaystyle \lambda _{1}={\frac {1}{2}}(-(-3.2)+{\sqrt {(-3.2)^{2}-4(2.56)}})=1.6\!}
λ
2
=
1
2
(
−
(
−
3.2
)
−
(
−
3.2
)
2
−
4
(
2.56
)
)
=
1.6
{\displaystyle \lambda _{2}={\frac {1}{2}}(-(-3.2)-{\sqrt {(-3.2)^{2}-4(2.56)}})=1.6\!}
λ
1
=
λ
2
{\displaystyle \lambda _{1}=\lambda _{2}\!}
y
1
=
e
1.6
x
{\displaystyle y_{1}=e^{1.6x}\!}
y
2
=
u
y
1
{\displaystyle y_{2}=uy_{1}\!}
u
=
c
1
x
+
c
2
{\displaystyle u=c_{1}x+c_{2}\!}
y
2
=
(
c
1
x
+
c
2
)
y
1
{\displaystyle y_{2}=(c_{1}x+c_{2})y_{1}\!}
c
1
=
1
c
2
=
0
{\displaystyle c_{1}=1c_{2}=0\!}
y
2
=
(
x
+
0
)
y
1
{\displaystyle y_{2}=(x+0)y_{1}\!}
y
2
=
x
y
1
{\displaystyle y_{2}=xy_{1}\!}
y
2
=
x
e
1.6
x
{\displaystyle y_{2}=xe^{1.6x}\!}
y
=
(
c
1
+
c
2
x
)
e
1.6
x
{\displaystyle y=(c_{1}+c_{2}x)e^{1.6x}\!}
General Solution
Check by Substitution
y
″
=
2.56
c
1
e
1.6
x
+
1.6
c
2
e
1.6
x
+
1.6
c
2
x
e
1.6
x
+
2.56
c
2
x
e
1.6
x
{\displaystyle y''=2.56c_{1}e^{1.6x}+1.6c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x}+2.56c_{2}xe^{1.6x}\!}
y
′
=
1.6
c
1
e
1.6
x
+
c
2
e
1.6
x
+
1.6
c
2
x
e
1.6
x
{\displaystyle y'=1.6c_{1}e^{1.6x}+c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x}\!}
y
=
c
1
e
1.6
x
+
c
2
x
e
1.6
x
{\displaystyle y=c_{1}e^{1.6x}+c_{2}xe^{1.6x}\!}
10
(
2.56
c
1
e
1.6
x
+
1.6
c
2
e
1.6
x
+
1.6
c
2
x
e
1.6
x
+
2.56
c
2
x
e
1.6
x
)
−
32
(
1.6
c
1
e
1.6
x
+
c
2
e
1.6
x
+
1.6
c
2
x
e
1.6
x
)
+
25.6
(
c
1
e
1.6
x
+
c
2
x
e
1.6
x
)
=
0
{\displaystyle 10(2.56c_{1}e^{1.6x}+1.6c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x}+2.56c_{2}xe^{1.6x})-32(1.6c_{1}e^{1.6x}+c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x})+25.6(c_{1}e^{1.6x}+c_{2}xe^{1.6x})=0\!}
y
=
(
c
1
+
c
2
x
)
e
1.6
x
{\displaystyle y=(c_{1}+c_{2}x)e^{1.6x}\!}
Solved and typed by - Cynthia Hernandez
Problem 16, P 59 Kreyszig:
e
2.6
x
,
e
−
4.3
x
{\displaystyle e^{2.6x},e^{-4.3x}\!}
Problem 17, P 59 Kreyszig:
e
−
5
x
,
x
e
−
5
x
{\displaystyle e^{-{\sqrt {5}}x},xe^{-{\sqrt {5}}x}\!}
Problem 16, P 59 Kreyszig:
ODE in the form:
y
″
+
a
y
′
+
b
y
=
0
{\displaystyle {y}''+a{y}'+by=0\!}
Problem 17, P 59 Kreyszig:
ODE in the form:
y
″
+
a
y
′
+
b
y
=
0
{\displaystyle {y}''+a{y}'+by=0\!}
Problem 16, P 59 Kreyszig:
For two distinct real-roots:
y
=
c
1
e
λ
1
x
+
c
2
e
λ
2
x
{\displaystyle y=c_{1}e^{\lambda _{1}x}+c_{2}e^{\lambda _{2}x}\!}
Where:
λ
1
=
2.6
{\displaystyle \lambda _{1}=2.6\!}
λ
2
=
−
4.3
{\displaystyle \lambda _{2}=-4.3\!}
The characteristic equation is:
λ
2
+
a
λ
+
b
=
0
{\displaystyle \lambda ^{2}+a\lambda +b=0\!}
Multiplying the roots of the equation together:
(
λ
−
2.6
)
(
λ
+
4.3
)
=
λ
2
+
1.7
λ
−
11.18
{\displaystyle (\lambda -2.6)(\lambda +4.3)=\lambda ^{2}+1.7\lambda -11.18\!}
Therefore the ODE is:
y
″
+
1.7
y
′
−
11.18
y
=
0
{\displaystyle y''+1.7y'-11.18y=0\!}
Problem 17, P 59 Kreyszig:
For real double root:
y
=
(
c
1
+
c
2
x
)
e
λ
x
{\displaystyle y=(c_{1}+c_{2}x)e^{\lambda x}\!}
Where:
λ
=
−
5
{\displaystyle \lambda =-{\sqrt {5}}\!}
The characteristic equation is:
λ
2
+
a
λ
+
b
=
0
{\displaystyle \lambda ^{2}+a\lambda +b=0\!}
Multiplying the roots of the equation together:
(
λ
+
5
)
2
=
λ
2
+
2
5
λ
+
5
{\displaystyle (\lambda +{\sqrt {5}})^{2}=\lambda ^{2}+2{\sqrt {5}}\lambda +5\!}
Therefore the ODE is:
y
″
+
2
5
y
′
+
5
y
=
0
{\displaystyle y''+2{\sqrt {5}}y'+5y=0\!}
Solved and typed by - Neil Tidwell 1:55, 06 February 2012 (UTC)
Spring-Dashpot-Mass System from Sec 1 lecture notes.
Has double real root
λ
=
−
3
{\displaystyle \lambda =-3\!}
k
,
c
,
m
{\displaystyle k,c,m\!}
For spring-mass-dashpot system:
m
(
y
k
″
+
k
c
y
k
′
)
+
k
y
k
=
f
(
t
)
{\displaystyle m(y_{k}''+{\frac {k}{c}}y_{k}')+ky_{k}=f(t)\!}
This simplifies to:
y
k
″
+
k
m
c
y
k
′
+
k
m
y
k
=
f
(
t
)
{\displaystyle y_{k}''+{\frac {k}{mc}}y_{k}'+{\frac {k}{m}}y_{k}=f(t)\!}
Multiply roots together to get characteristic equation:
(
λ
+
3
)
2
=
λ
2
+
6
λ
+
9
{\displaystyle (\lambda +3)^{2}=\lambda ^{2}+6\lambda +9\!}
Set coefficients of simplified spring-mass-dashpot equation equal to those of characteristic equation:
k
m
c
=
6
{\displaystyle {\frac {k}{mc}}=6\!}
k
m
=
9
{\displaystyle {\frac {k}{m}}=9\!}
Have one degree of freedom, so arbitrarily choose
m
=
1
{\displaystyle m=1\!}
Solve system:
m
=
1
{\displaystyle m=1\!}
k
=
9
{\displaystyle k=9\!}
c
=
1.5
{\displaystyle c=1.5\!}
Solved and typed by - Neil Tidwell 2:14, 06 February 2012 (UTC)
Develop the MacLaurin Series (Taylor Series at
t
=
0
{\displaystyle t=0\!}
e
t
,
cos
t
,
sin
t
{\displaystyle e^{t},\cos t,\sin t\!}
L
[
y
]
a
n
d
L
[
w
]
t
h
e
n
L
[
y
+
w
]
{\displaystyle L[y]andL[w]thenL[y+w]\!}
L
[
y
+
w
]
=
L
[
y
]
+
L
[
w
]
{\displaystyle L[y+w]=L[y]+L[w]\!}
L
[
c
y
]
=
c
L
[
y
]
{\displaystyle L[cy]=cL[y]}
L
[
k
w
]
=
k
L
[
w
]
{\displaystyle L[kw]=kL[w]\!}
Solved and typed by - Jenny Schulze
Find a general solution to the equations, and check answers by substitution.Problem 8
y
″
+
y
′
+
3.25
y
=
0
{\displaystyle y''+y'+3.25y=0\!}
(8.0)
Problem 15
y
″
+
0.54
y
′
+
(
0.0729
+
π
)
y
=
0
{\displaystyle y''+0.54y'+(0.0729+\pi )y=0\!}
(8.1)
Factor as in the text and solve.
Solved and typed by - Jenny Schulze
Initial Conditions:
y
(
0
)
=
1
,
y
′
(
0
)
=
0
{\displaystyle y(0)=1,y'(0)=0\ }
No excitation:
r
(
x
)
=
0
{\displaystyle r(x)=0\ }
Find and plot the solution for the L2-ODE-CC corresponding to:
λ
2
+
4
λ
+
13
=
0
{\displaystyle \lambda ^{2}+4\lambda +13=0\!}
In another Fig., superimpose 3 Figs.: (a) this Fig., (b) the Fig. in R2.6 p.5-6, (c) the Fig. in R2.1 p.3-7.
The corresponding ODE in standard form:
y
″
+
4
y
′
+
13
y
=
r
(
x
)
{\displaystyle y''+4y'+13y=r(x)\!}
a
λ
2
+
b
λ
+
c
=
0
{\displaystyle a\lambda ^{2}+b\lambda +c=0\!}
which in this case is:
λ
2
+
4
λ
+
13
=
0
{\displaystyle \lambda ^{2}+4\lambda +13=0\!}
use the formula to find the roots:
λ
1
,
2
=
−
b
±
i
b
2
−
4
a
c
2
a
=
−
α
±
i
ω
{\displaystyle \lambda _{1,2}={\frac {-b\pm i{\sqrt {b^{2}-4ac}}}{2a}}=-\alpha \pm i\omega }
λ
1
,
2
=
−
4
±
i
4
2
−
4
∗
1
∗
13
2
∗
1
=
−
2
±
3
i
{\displaystyle \lambda _{1,2}={\frac {-4\pm i{\sqrt {4^{2}-4*1*13}}}{2*1}}=-2\pm 3i}
because the roots are complex conjugates, the general solution can be given as:
y
(
t
)
=
e
−
α
t
(
A
c
o
s
ω
t
+
b
s
i
n
ω
t
)
=
e
−
2
t
(
A
c
o
s
3
t
+
B
s
i
n
3
t
)
{\displaystyle y(t)=e^{-\alpha t}(Acos\omega t+bsin\omega t)=e^{-2t}(Acos3t+Bsin3t)\!}
to find A and B, we use the initial conditions and take the first derivative of y(t):
y
(
0
)
=
1
=
e
−
2
∗
0
(
A
c
o
s
(
3
∗
0
)
+
B
s
i
n
(
3
∗
0
)
=
1
∗
A
=
A
{\displaystyle y(0)=1=e^{-2*0}(Acos(3*0)+Bsin(3*0)=1*A=A\!}
A
=
1
{\displaystyle A=1\!}
y
′
(
t
)
=
e
−
2
t
(
(
−
2
A
+
3
B
)
c
o
s
(
3
t
)
−
(
3
A
+
2
B
)
s
i
n
(
3
t
)
)
{\displaystyle y'(t)=e^{-2t}((-2A+3B)cos(3t)-(3A+2B)sin(3t))\!}
y
′
(
0
)
=
0
=
e
−
2
∗
0
(
(
−
2
∗
1
+
3
B
)
c
o
s
(
3
∗
0
)
−
(
3
∗
1
+
2
B
)
s
i
n
(
3
∗
0
)
)
=
1
∗
(
−
2
+
3
B
)
=
−
2
+
3
B
{\displaystyle y'(0)=0=e^{-2*0}((-2*1+3B)cos(3*0)-(3*1+2B)sin(3*0))=1*(-2+3B)=-2+3B\!}
B
=
2
3
{\displaystyle B={\frac {2}{3}}\!}
thus:
y
(
t
)
=
e
−
2
t
(
c
o
s
3
t
+
2
3
s
i
n
3
t
)
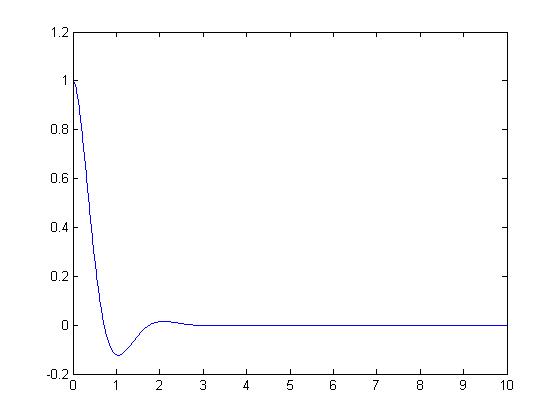
{\displaystyle y(t)=e^{-2t}(cos3t+{\frac {2}{3}}sin3t)\!}
The graph of the solved equation is shown below in Fig. 1.
The three graphed equations are shown together below in Fig. 2
y
1
(
t
)
=
e
−
2
t
(
c
o
s
3
t
+
2
3
s
i
n
3
t
)
{\displaystyle y_{1}(t)=e^{-2t}(cos3t+{\frac {2}{3}}sin3t)\!}
Equation 2 (R2.6):
y
2
(
t
)
=
e
−
3
t
+
3
t
e
−
3
t
{\displaystyle y_{2}(t)=e^{-3t}+3te^{-3t}\!}
Equation 3 (R2.1):
y
3
(
t
)
=
5
7
e
−
2
t
+
2
7
e
5
t
{\displaystyle y_{3}(t)={\frac {5}{7}}e^{-2t}+{\frac {2}{7}}e^{5t}\!}
Solved and typed by - --James Moncrief 01:42, 8 February 2012 (UTC)





























































































































![{\displaystyle L[y]andL[w]thenL[y+w]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72d1b059fee3a82b2cef1e4ea552da52c14f51b5)
![{\displaystyle L[y+w]=L[y]+L[w]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25cec511be783207b072ddba15227be77c3fc645)
![{\displaystyle L[cy]=cL[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d212bdd9ffbe58ae0eb7e770a4ec817a581f28f6)
![{\displaystyle L[kw]=kL[w]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bd6ff53b66fc05d1fd242f184e6ff160f1617bc)