University of Florida/Egm4313/s12.team11.imponenti/R2.2

Report 2, Problem 2

Problem Statement

Find and plot the solution for the homogeneous L2-ODE-CC

$y''(x)-10y'(x)+25y(x)=0\!$

with initial conditions $y(0)=1\!$ ,and $y'(0)=0\!$

Characteristic Equation

$\lambda ^{2}-10\lambda +25=0\!$

$(\lambda -5)(\lambda -5)=0\!$

$\lambda =5\!$

Homogeneous Solution

The solution to a L2-ODE-CC with real double root is given by

$y(x)=c_{1}e^{\lambda x}+c_{2}xe^{\lambda x}\!$

First initial condition

$y(0)=1\!$

$y(0)=c_{1}e^{5*0}+c_{2}*0*e^{5*0}=1\!$

$c_{1}=1\!$

Second initial condition

$y'(0)=0\!$

${\frac {d}{dx}}y(x)=y'(x)=5e^{5x}+c_{2}e^{5x}(5x+1)\!$

$y'(0)=5e^{5*0}+c_{2}e^{5*0}(5*0+1)=0\!$

$5+c_{2}=0\!$

$c_{2}=-5\!$

The solution to our L2-ODE-CC is

                       $y(x)=e^{5x}(1-5x)\!$

Plot

$y(x)=e^{5x}(1-5x)\!$

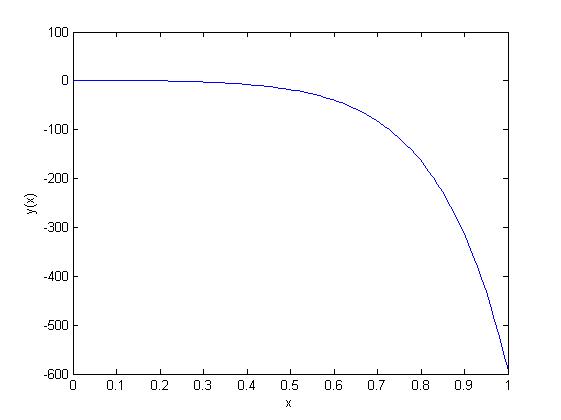
Egm4313.s12.team11.imponenti 00:30, 8 February 2012 (UTC)