Report 7
Intermediate Engineering Analysis
Section 7566
Team 11
Due date: April 25, 2012.
Solved by Andrea Vargas
Verify (4)-(5) pg 19-9:
(4)  for
for 
(5)  for
for 
From the lecture notes on p.19-9 we know that:
(2) 
(3) 
Then, we have

Since the period of  is
is  and we know that
and we know that  , we can assume that
, we can assume that  for simplicity.
for simplicity.
We can compute the result of the previous integral using Wolfram ALpha (Mathematica software). The following is the input given to the software:
int from 0 to pi sin(ax)sin(bx)
where a is  and b is
and b is  . The software generates the following answer:
. The software generates the following answer:

Substituting for  and
and  :
:

We also know that  where c is any integer. We can cancel any terms with
where c is any integer. We can cancel any terms with  or
or  as they are equal to zero.
as they are equal to zero.
Then, we can verify:
(4)  for
for 
Similarly we can verify (5).
We have

Here, we will keep the integration boundaries as  to be consistent with the problem statement.
to be consistent with the problem statement.
We can compute the result of the previous integral using Wolfram ALpha (Mathematica software). The following is the input given to the software:
int 0 to L (sin(ax))^2
where a is  . The software generates the following answer:
. The software generates the following answer:

Substituting for  :
:

We know from the previous explanation that  .So,we can apply the same assumption as before that
.So,we can apply the same assumption as before that  where c is any integer. This allows us to cancel any terms with
where c is any integer. This allows us to cancel any terms with  as they are equal to zero.
as they are equal to zero.
Then, we can verify:
(5)  for
for 
Solved by Francisco Arrieta
Plot the truncated series  with
with  and for:
and for:


Using:

Then:

![{\displaystyle =2\left[{\frac {(-1)^{j}-1}{\pi ^{3}j^{3}}}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b9edee1735a65c4e8e77e0fe0d8c56c42df298c)
 for all even values of j
for all even values of j
Plugging back to the truncated series:
![{\displaystyle u(x,t)=\sum _{j=1}^{n}2\left[{\frac {(-1)^{j}-1}{\pi ^{3}j^{3}}}\right]\cos[C{\frac {j\pi }{L}}\alpha {\frac {2L}{C}}]\sin[{\frac {j\pi }{L}}x]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3e5da7427b39a2b47f74c890be6daa36b4584c)
![{\displaystyle =\sum _{j=1}^{n}2\left[{\frac {(-1)^{j}-1}{\pi ^{3}j^{3}}}\right]\cos(\alpha j2\pi )\sin({\frac {j\pi }{2}}x)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d178327c761aef07b1e905e1b7cc8c4a17f83d)
For  :
:
![{\displaystyle u(x,t)=[{\frac {-4}{\pi ^{3}}}\cos(2\pi \alpha )\sin({\frac {\pi x}{2}})]+[{\frac {-4}{27\pi ^{3}}}\cos(6\pi \alpha )\sin({\frac {3\pi x}{2}})]+[{\frac {-4}{125\pi ^{3}}}\cos(10\pi \alpha )\sin({\frac {5\pi x}{2}})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecbb2bafe8d86dfbd5fb43ce8281b85f2833499a)
When  :
:

When  :
:

When  :
:
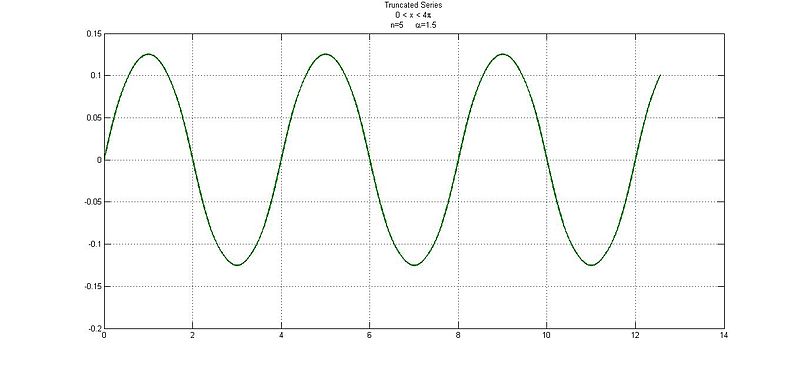
When  :
:

--Egm4313.s12.team11.arrieta (talk) 06:20, 22 April 2012 (UTC)
Find (a) the scalar product, (b) the magnitude of  and
and  ,(c) the angle between
,(c) the angle between  and
and  for:
for:
1) 
2) 
solved by Kyle Gooding


Using integration by parts;
![{\displaystyle <f,g>=[x\sin(x)+\cos(x)]_{-2}^{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06ebb57cd5e38e25a1c85810efce7780355558e0)


![{\displaystyle =\int _{-2}^{10}[\cos(x)]^{2}\ dx\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b9fed1f7272d0c3ded1fd8e5370e7c8722806eb)
![{\displaystyle =[.5(x+\sin(x)\cos(x)|_{-2}^{10}]^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28efb2c181e6b7c741e4acd76bdd1ad27d91076f)



![{\displaystyle =[x^{3}/3]_{-2}^{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d38251d182847ee8da52d55a500779afb2a40d)




The two functions are nearly orthogonal.
solved by Luca Imponenti

![{\displaystyle <f,g>=\int _{-1}^{1}[{\frac {1}{2}}(3x^{2}-1)][{\frac {1}{2}}(5x^{3}-3x)]\ dx\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfc6e327a734ba8f03bbf1230e50e5e98223f28f)


![{\displaystyle ={\frac {1}{4}}[({\frac {15}{6}}1^{6}-1^{4}+{\frac {3}{2}}1^{2})-({\frac {15}{6}}(-1)^{6}-(-1)^{4}+{\frac {3}{2}}(-1)^{2})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53cff8357d3b5f93f2fbaae853728c278b35d84e)
Since all exponents are even, everything in brackets cancels out


![{\displaystyle =\int _{-1}^{1}[{\frac {1}{2}}(3x^{2}-1)]^{2}\ dx\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96ccb23d62629ff7917a2a6e03e2a6750c6a1cb2)


![{\displaystyle ={\frac {1}{4}}[({\frac {9}{5}}1^{5}-2(1)^{3}+1)-({\frac {9}{5}}(-1)^{5}-2(-1)^{3}+(-1))]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a67a46b3168d49f86e6b9d5193940336b666e72)
![{\displaystyle ={\frac {1}{4}}[{\frac {4}{5}}-(-{\frac {4}{5}})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c25eee2b658f4822793325fe55dbe628ec494f4e)


![{\displaystyle =\int _{-1}^{1}[{\frac {1}{2}}(5x^{3}-3x)]^{2}\ dx\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7dab4c84a1b03ac40fba4b50302dfb4d1a45262)


![{\displaystyle ={\frac {1}{4}}[({\frac {25}{7}}1^{7}-6(1)^{5}+3(1)^{3})-({\frac {25}{7}}(-1)^{7}-6(-1)^{5}+3(-1)^{3})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4531b4d40107736928a68a1c13e726c81505e0f)
![{\displaystyle ={\frac {1}{4}}[{\frac {4}{7}}-(-{\frac {4}{7}})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dc29b7811deeaa641b8e5ecbb01cb934edd33a2)


Since  the two functions are orthogonal
the two functions are orthogonal

Solved by Gonzalo Perez
Sketch or graph  which for
which for  is given as follows:
is given as follows:

The MATLAB code shown below was used to developed the graph of  :
:


Sketch or graph  which for
which for  is given as follows:
is given as follows:

The MATLAB code shown below was used to developed the graph of the piecewise function  :
:


Solved by Jonathan Sheider
Find the Fourier series of the given function which is assumed to have a period of  . Show the details of your work.
. Show the details of your work.
Sketch or graph the partial sums up to that including  and
and 
Given:

The Fourier series of a function with a period of  is defined:
is defined:

Where:



This particular function given in the problem can be also defined in a piecewise manner over this interval, namely:

Calculating the first term  :
:

![{\displaystyle a_{0}={\frac {1}{2\pi }}\left(\left[{\frac {-x^{2}}{2}}\right]_{-\pi }^{0}+\left[{\frac {x^{2}}{2}}\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e17df4be9800f3431026f88698aeddb9583aec3)



Calculating the coefficient  :
:


Using integration by parts with the following substitutions:
 and therefore
and therefore 
 and therefore
and therefore 
This yields for the integral:
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(-\left[{\frac {1}{n}}xsin(nx)-\int {\frac {1}{n}}sin(nx)dx\right]_{-\pi }^{0}+\left[{\frac {1}{n}}xsin(nx)-\int {\frac {1}{n}}sin(nx)dx\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f207735cd3f6a76889368cf0bcffbae9093c82)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(-\left[{\frac {1}{n}}xsin(nx)+{\frac {1}{n^{2}}}cos(nx)\right]_{-\pi }^{0}+\left[{\frac {1}{n}}xsin(nx)+{\frac {1}{n^{2}}}cos(nx)\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2b633c9c87057353bf6ee823049d2b4c115a542)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(-\left[{\frac {1}{n^{2}}}-\left({\frac {1}{n}}(-\pi )sin(-n\pi )+{\frac {1}{n^{2}}}cos(-n\pi )\right)\right]+\left[{\frac {1}{n}}\pi sin(n\pi )+{\frac {1}{n^{2}}}cos(n\pi )-{\frac {1}{n^{2}}}\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d9959d8d3079033c212a612dfe6e0701340f3d)
Note that for all n = 1,2,3... :  as
as  therefore these terms are evaluated as zero, which yields:
therefore these terms are evaluated as zero, which yields:
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(-\left[{\frac {1}{n^{2}}}-\left(0+{\frac {1}{n^{2}}}cos(-n\pi )\right)\right]+\left[0+{\frac {1}{n^{2}}}cos(n\pi )-{\frac {1}{n^{2}}}\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d8a40694482606047531daefc07e8dc0137c4ad)

Note that  therefore:
therefore:




To evaluate the term  :
:
Note that  for odd n values as
for odd n values as 
And that  for even n values as
for even n values as  .
.
Therefore, it can be concluded that for odd n values:

And for even n values:

Therefore, for the coefficient  , all even terms will equal zero while all odd terms will have a multiplier of 2, this yields (for all odd n values):
, all even terms will equal zero while all odd terms will have a multiplier of 2, this yields (for all odd n values):

Calculating the coefficient  :
:


Using integration by parts with the following substitutions:
 and therefore
and therefore 
 and therefore
and therefore 
This yields for the integral:
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(-\left[{\frac {-1}{n}}xcos(nx)-\int {\frac {-1}{n}}cos(nx)dx\right]_{-\pi }^{0}+\left[{\frac {-1}{n}}xcos(nx)-\int {\frac {-1}{n}}cos(nx)dx\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/975903e802e5abdabbcb2ba1c3195f0fdacd3607)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(-\left[{\frac {-1}{n}}xcos(nx)+{\frac {1}{n^{2}}}sin(nx)\right]_{-\pi }^{0}+\left[{\frac {-1}{n}}xcos(nx)+{\frac {1}{n^{2}}}sin(nx)\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68fecd9942e380ab24ceae33d529c500cec18c82)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(-\left[0-\left({\frac {-1}{n}}(-\pi )cos(-n\pi )+{\frac {1}{n^{2}}}sin(-n\pi )\right)\right]+\left[{\frac {-1}{n}}\pi cos(n\pi )+{\frac {1}{n^{2}}}sin(n\pi )-0\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95ab7b425606a7908018f24b660d5e5cd7f3caa9)
Note that for all n = 1,2,3... :  as
as  therefore these terms are evaluated as zero, which yields:
therefore these terms are evaluated as zero, which yields:
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(-\left[0-\left({\frac {-1}{n}}(-\pi )cos(-n\pi )+0\right)\right]+\left[{\frac {-1}{n}}\pi cos(n\pi )+0\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e42a5d3165b5afa0d7c91bd861e6184a01a373b)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n}}(\pi )cos(-n\pi )\right]+\left[{\frac {-1}{n}}\pi cos(n\pi )\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/347593712464e1543f4132ae4cb28e07450c530d)
Note that  therefore:
therefore:



Therefore there will be no  terms in the Fourier representation.
In conclusion, the Fourier series representation for the given function is as follows:
terms in the Fourier representation.
In conclusion, the Fourier series representation for the given function is as follows:


A graph of the function, and the Fourier series for  is shown below:
is shown below:
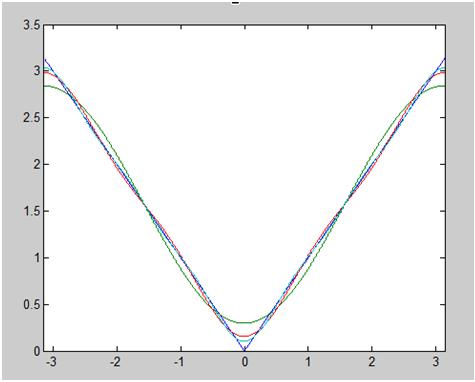
--Egm4313.s12.team11.sheider (talk) 06:00, 22 April 2012 (UTC)
Find the Fourier series of the given function which is assumed to have a period of  . Show the details of your work.
. Show the details of your work.
Sketch or graph the partial sums up to that including  and
and 
Given:

The Fourier series of a function with a period of  is defined:
is defined:

Where:



Calculating the first term  :
:

![{\displaystyle a_{0}={\frac {1}{2\pi }}\left(\left[{\frac {x^{2}}{2}}\right]_{-\pi }^{0}+\left[\pi x-{\frac {x^{2}}{2}}\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af09909b1e049b7124b5d70c419623a1149ee34f)




Calculating the coefficient  :
:

Using integration by parts with the following substitutions for the integral  :
:
 and therefore
and therefore 
 and therefore
and therefore 
Using integration by parts with the following substitutions for the integral  :
:
 and therefore
and therefore 
 and therefore
and therefore 
This yields for the overall expression:
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n}}xsin(nx)-\int {\frac {1}{n}}sin(nx)dx\right]_{-\pi }^{0}+\left[{\frac {1}{n}}(\pi -x)sin(nx)-\int -{\frac {1}{n}}sin(nx)dx\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e6b3207229bdc26ff5d126f3958fa7bcb0a47ce)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n}}xsin(nx)+{\frac {1}{n^{2}}}cos(nx)\right]_{-\pi }^{0}+\left[{\frac {1}{n}}(\pi -x)sin(nx)-{\frac {1}{n^{2}}}cos(nx)\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/790cd72d4dced9490edb09171b99475fcde079c5)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n^{2}}}-\left({\frac {1}{n}}(-\pi )sin(-n\pi )+{\frac {1}{n^{2}}}cos(-n\pi )\right)\right]+\left[-{\frac {1}{n^{2}}}cos(n\pi )+{\frac {1}{n^{2}}}\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5184b16af9520d7856eeb6a65c90aa3c1950b99b)
Note that for all n = 1,2,3... :  as
as  therefore these terms are evaluated as zero, which yields:
therefore these terms are evaluated as zero, which yields:
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n^{2}}}-0-{\frac {1}{n^{2}}}cos(-n\pi )\right]+\left[-{\frac {1}{n^{2}}}cos(n\pi )+{\frac {1}{n^{2}}}\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/345a49f8d9cfaa705639ff511d9e4376e59ae97e)

Note that  therefore:
therefore:




To evaluate the term  :
:
Note that  for odd n values as
for odd n values as 
And that  for even n values as
for even n values as  .
.
Therefore, it can be concluded that for odd n values:

And for even n values:

Therefore, for the coefficient  , all even terms will equal zero while all odd terms will have a multiplier of 2, this yields (for all odd n values):
, all even terms will equal zero while all odd terms will have a multiplier of 2, this yields (for all odd n values):

Calculating the coefficient  :
:

Using integration by parts with the following substitutions for the integral  :
:
 and therefore
and therefore 
 and therefore
and therefore 
Using integration by parts with the following substitutions for the integral  :
:
 and therefore
and therefore 
 and therefore
and therefore 
This yields for the overall expression:
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(\left[{\frac {-1}{n}}xcos(nx)-\int {\frac {-1}{n}}cos(nx)dx\right]_{-\pi }^{0}+\left[{\frac {-1}{n}}(\pi -x)cos(nx)-\int -{\frac {-1}{n}}cos(nx)dx\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00a82d3af7cc8e00ce618d200c082ce312b8f3cd)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(\left[{\frac {-1}{n}}xcos(nx)+{\frac {1}{n^{2}}}sin(nx)\right]_{-\pi }^{0}+\left[{\frac {-1}{n}}(\pi -x)cos(nx)-{\frac {1}{n^{2}}}sin(nx)\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9beafbe721d90b04eb33c2221973042d165ed8b4)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(\left[0-\left({\frac {-1}{n}}(-\pi )cos(-n\pi )+{\frac {1}{n^{2}}}sin(-n\pi )\right)\right]+\left[-{\frac {1}{n^{2}}}sin(n\pi )-\left({\frac {-1}{n}}\pi \right)\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d1dee6e11e995af845e98577345badbea5d4243)

Note that for all n = 1,2,3... :  as
as  therefore these terms are evaluated as zero, which yields:
therefore these terms are evaluated as zero, which yields:


Note that  therefore:
therefore:



To evaluate the term  :
:
Note that  for odd n values as
for odd n values as 
And that  for even n values as
for even n values as  .
.
Therefore, it can be concluded that for odd n values:

And for even n values:

Therefore, for the coefficient  , all even terms will equal zero while all odd terms will have a multiplier of 2, this yields (for all odd n values):
, all even terms will equal zero while all odd terms will have a multiplier of 2, this yields (for all odd n values):

In conclusion, the Fourier series representation for the given function is as follows:


A graph of the function, and the Fourier series for  is shown below:
is shown below:

--Egm4313.s12.team11.sheider (talk) 06:00, 22 April 2012 (UTC)
Solved by Daniel Suh
Consider the following,


with  , and
, and 
1. Find the integration with the given data.
2. Confirm the results with Matlab's trapz command for the trapezoidal rule.
Angle Sum and Difference Identities


Rearrange


Substitute and Combine










>> X = 0:2*pi/100:2*pi;
>> Y = sin(2*X).*sin(3*X);
>> Z = trapz(X,Y)
Z =
2.9490e-017
































![{\displaystyle =2\left[{\frac {(-1)^{j}-1}{\pi ^{3}j^{3}}}\right]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b9edee1735a65c4e8e77e0fe0d8c56c42df298c)

![{\displaystyle u(x,t)=\sum _{j=1}^{n}2\left[{\frac {(-1)^{j}-1}{\pi ^{3}j^{3}}}\right]\cos[C{\frac {j\pi }{L}}\alpha {\frac {2L}{C}}]\sin[{\frac {j\pi }{L}}x]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3e5da7427b39a2b47f74c890be6daa36b4584c)
![{\displaystyle =\sum _{j=1}^{n}2\left[{\frac {(-1)^{j}-1}{\pi ^{3}j^{3}}}\right]\cos(\alpha j2\pi )\sin({\frac {j\pi }{2}}x)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d178327c761aef07b1e905e1b7cc8c4a17f83d)
![{\displaystyle u(x,t)=[{\frac {-4}{\pi ^{3}}}\cos(2\pi \alpha )\sin({\frac {\pi x}{2}})]+[{\frac {-4}{27\pi ^{3}}}\cos(6\pi \alpha )\sin({\frac {3\pi x}{2}})]+[{\frac {-4}{125\pi ^{3}}}\cos(10\pi \alpha )\sin({\frac {5\pi x}{2}})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecbb2bafe8d86dfbd5fb43ce8281b85f2833499a)














![{\displaystyle <f,g>=[x\sin(x)+\cos(x)]_{-2}^{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06ebb57cd5e38e25a1c85810efce7780355558e0)


![{\displaystyle =\int _{-2}^{10}[\cos(x)]^{2}\ dx\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b9fed1f7272d0c3ded1fd8e5370e7c8722806eb)
![{\displaystyle =[.5(x+\sin(x)\cos(x)|_{-2}^{10}]^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28efb2c181e6b7c741e4acd76bdd1ad27d91076f)



![{\displaystyle =[x^{3}/3]_{-2}^{10}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d38251d182847ee8da52d55a500779afb2a40d)




![{\displaystyle <f,g>=\int _{-1}^{1}[{\frac {1}{2}}(3x^{2}-1)][{\frac {1}{2}}(5x^{3}-3x)]\ dx\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfc6e327a734ba8f03bbf1230e50e5e98223f28f)


![{\displaystyle ={\frac {1}{4}}[({\frac {15}{6}}1^{6}-1^{4}+{\frac {3}{2}}1^{2})-({\frac {15}{6}}(-1)^{6}-(-1)^{4}+{\frac {3}{2}}(-1)^{2})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53cff8357d3b5f93f2fbaae853728c278b35d84e)

![{\displaystyle =\int _{-1}^{1}[{\frac {1}{2}}(3x^{2}-1)]^{2}\ dx\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96ccb23d62629ff7917a2a6e03e2a6750c6a1cb2)


![{\displaystyle ={\frac {1}{4}}[({\frac {9}{5}}1^{5}-2(1)^{3}+1)-({\frac {9}{5}}(-1)^{5}-2(-1)^{3}+(-1))]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a67a46b3168d49f86e6b9d5193940336b666e72)
![{\displaystyle ={\frac {1}{4}}[{\frac {4}{5}}-(-{\frac {4}{5}})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c25eee2b658f4822793325fe55dbe628ec494f4e)

![{\displaystyle =\int _{-1}^{1}[{\frac {1}{2}}(5x^{3}-3x)]^{2}\ dx\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7dab4c84a1b03ac40fba4b50302dfb4d1a45262)


![{\displaystyle ={\frac {1}{4}}[({\frac {25}{7}}1^{7}-6(1)^{5}+3(1)^{3})-({\frac {25}{7}}(-1)^{7}-6(-1)^{5}+3(-1)^{3})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4531b4d40107736928a68a1c13e726c81505e0f)
![{\displaystyle ={\frac {1}{4}}[{\frac {4}{7}}-(-{\frac {4}{7}})]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dc29b7811deeaa641b8e5ecbb01cb934edd33a2)





















![{\displaystyle a_{0}={\frac {1}{2\pi }}\left(\left[{\frac {-x^{2}}{2}}\right]_{-\pi }^{0}+\left[{\frac {x^{2}}{2}}\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e17df4be9800f3431026f88698aeddb9583aec3)










![{\displaystyle a_{n}={\frac {1}{\pi }}\left(-\left[{\frac {1}{n}}xsin(nx)-\int {\frac {1}{n}}sin(nx)dx\right]_{-\pi }^{0}+\left[{\frac {1}{n}}xsin(nx)-\int {\frac {1}{n}}sin(nx)dx\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f207735cd3f6a76889368cf0bcffbae9093c82)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(-\left[{\frac {1}{n}}xsin(nx)+{\frac {1}{n^{2}}}cos(nx)\right]_{-\pi }^{0}+\left[{\frac {1}{n}}xsin(nx)+{\frac {1}{n^{2}}}cos(nx)\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2b633c9c87057353bf6ee823049d2b4c115a542)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(-\left[{\frac {1}{n^{2}}}-\left({\frac {1}{n}}(-\pi )sin(-n\pi )+{\frac {1}{n^{2}}}cos(-n\pi )\right)\right]+\left[{\frac {1}{n}}\pi sin(n\pi )+{\frac {1}{n^{2}}}cos(n\pi )-{\frac {1}{n^{2}}}\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32d9959d8d3079033c212a612dfe6e0701340f3d)


![{\displaystyle a_{n}={\frac {1}{\pi }}\left(-\left[{\frac {1}{n^{2}}}-\left(0+{\frac {1}{n^{2}}}cos(-n\pi )\right)\right]+\left[0+{\frac {1}{n^{2}}}cos(n\pi )-{\frac {1}{n^{2}}}\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d8a40694482606047531daefc07e8dc0137c4ad)



















![{\displaystyle b_{n}={\frac {1}{\pi }}\left(-\left[{\frac {-1}{n}}xcos(nx)-\int {\frac {-1}{n}}cos(nx)dx\right]_{-\pi }^{0}+\left[{\frac {-1}{n}}xcos(nx)-\int {\frac {-1}{n}}cos(nx)dx\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/975903e802e5abdabbcb2ba1c3195f0fdacd3607)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(-\left[{\frac {-1}{n}}xcos(nx)+{\frac {1}{n^{2}}}sin(nx)\right]_{-\pi }^{0}+\left[{\frac {-1}{n}}xcos(nx)+{\frac {1}{n^{2}}}sin(nx)\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68fecd9942e380ab24ceae33d529c500cec18c82)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(-\left[0-\left({\frac {-1}{n}}(-\pi )cos(-n\pi )+{\frac {1}{n^{2}}}sin(-n\pi )\right)\right]+\left[{\frac {-1}{n}}\pi cos(n\pi )+{\frac {1}{n^{2}}}sin(n\pi )-0\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95ab7b425606a7908018f24b660d5e5cd7f3caa9)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(-\left[0-\left({\frac {-1}{n}}(-\pi )cos(-n\pi )+0\right)\right]+\left[{\frac {-1}{n}}\pi cos(n\pi )+0\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e42a5d3165b5afa0d7c91bd861e6184a01a373b)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n}}(\pi )cos(-n\pi )\right]+\left[{\frac {-1}{n}}\pi cos(n\pi )\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/347593712464e1543f4132ae4cb28e07450c530d)









![{\displaystyle a_{0}={\frac {1}{2\pi }}\left(\left[{\frac {x^{2}}{2}}\right]_{-\pi }^{0}+\left[\pi x-{\frac {x^{2}}{2}}\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af09909b1e049b7124b5d70c419623a1149ee34f)









![{\displaystyle a_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n}}xsin(nx)-\int {\frac {1}{n}}sin(nx)dx\right]_{-\pi }^{0}+\left[{\frac {1}{n}}(\pi -x)sin(nx)-\int -{\frac {1}{n}}sin(nx)dx\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e6b3207229bdc26ff5d126f3958fa7bcb0a47ce)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n}}xsin(nx)+{\frac {1}{n^{2}}}cos(nx)\right]_{-\pi }^{0}+\left[{\frac {1}{n}}(\pi -x)sin(nx)-{\frac {1}{n^{2}}}cos(nx)\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/790cd72d4dced9490edb09171b99475fcde079c5)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n^{2}}}-\left({\frac {1}{n}}(-\pi )sin(-n\pi )+{\frac {1}{n^{2}}}cos(-n\pi )\right)\right]+\left[-{\frac {1}{n^{2}}}cos(n\pi )+{\frac {1}{n^{2}}}\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5184b16af9520d7856eeb6a65c90aa3c1950b99b)
![{\displaystyle a_{n}={\frac {1}{\pi }}\left(\left[{\frac {1}{n^{2}}}-0-{\frac {1}{n^{2}}}cos(-n\pi )\right]+\left[-{\frac {1}{n^{2}}}cos(n\pi )+{\frac {1}{n^{2}}}\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/345a49f8d9cfaa705639ff511d9e4376e59ae97e)










![{\displaystyle b_{n}={\frac {1}{\pi }}\left(\left[{\frac {-1}{n}}xcos(nx)-\int {\frac {-1}{n}}cos(nx)dx\right]_{-\pi }^{0}+\left[{\frac {-1}{n}}(\pi -x)cos(nx)-\int -{\frac {-1}{n}}cos(nx)dx\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00a82d3af7cc8e00ce618d200c082ce312b8f3cd)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(\left[{\frac {-1}{n}}xcos(nx)+{\frac {1}{n^{2}}}sin(nx)\right]_{-\pi }^{0}+\left[{\frac {-1}{n}}(\pi -x)cos(nx)-{\frac {1}{n^{2}}}sin(nx)\right]_{0}^{\pi }\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9beafbe721d90b04eb33c2221973042d165ed8b4)
![{\displaystyle b_{n}={\frac {1}{\pi }}\left(\left[0-\left({\frac {-1}{n}}(-\pi )cos(-n\pi )+{\frac {1}{n^{2}}}sin(-n\pi )\right)\right]+\left[-{\frac {1}{n^{2}}}sin(n\pi )-\left({\frac {-1}{n}}\pi \right)\right]\right)\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d1dee6e11e995af845e98577345badbea5d4243)


























