Trigonometry/Angles
An angle is made of two rays with a common endpoint in a single plane.
All angles consist of a few primary parts: an initial and a terminal ray, and an angle measure.
The vertex of the angle is the point at which the initial and terminal ray intersect. Rotating about the vertex from the initial to the terminal ray gives the angle measure.
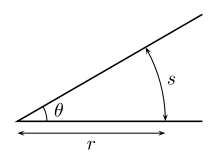
The measure of an angle is defined as the length of an arc between the initial ray and the terminal ray of a unit circle whose center is at the common end point. There are different ways to measure the size of an angle. It may be given in terms of :
- in radians, defined as the length of the arc described above, or
- in degrees, 1/360th of a circle.
An angle is frequently denoted by a greek letter, typically . When an angle is measured in radians, there is the following relationship between (the arc length on a circle cut off by that angle), (the radius of that circle), and measured in radians:
.
Using elementary algebra:
and
Thus, value of θ could be measured using any circle and not just the unit circle by taking the ratio of the arc length to the radius. Further the size of θ is independent of the size of the circle, since the ratio remains the same as the radius and arc length change proportionally. Also, with this interpretation of the angle measure, notice that the angle is measured by taking the ratio two quantities which would have the same units of measure namely, what ever units we are measuring length. As such the resulting angle measure is said to be unitless which has important ramifications in applied settings.
Reading: Wikipedia: Measuring Angles
Videos:
Introduction to angles
Angles (part 2)
Angles (part 3)
Radians and Degrees
Quiz: Quiz







