The
real sine function induces a
bijective,
strictly increasing
function
-
![{\displaystyle [-\pi /2,\pi /2]\longrightarrow [-1,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/527f8bc31212ec82e3778cde36b1ed32192bf657)
and the
real cosine function
induces a bijective, strictly decreasing function
-
![{\displaystyle [0,\pi ]\longrightarrow [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbd9728b307c63938254cd4e4aff49bc8e2f2a7)
Proof
The
real tangent function
induces a
bijective,
strictly increasing
function
-
![{\displaystyle ]-\pi /2,\pi /2[\longrightarrow \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54b80848470e2b293193379bd774648a7d69df6)
and the
real cotangent function
induces a bijective strictly decreasing function
-
![{\displaystyle [0,\pi ]\longrightarrow \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/014d0207862d72a4533c62948f6bae80d18e9964)
Proof
Due to the bijectivity of sine, cosine, tangent and cotangent on suitable interval, there exist the following inverse functions.
The
inverse function
of the real
sine function
is
-
![{\displaystyle [-1,1]\longrightarrow [-{\frac {\pi }{2}},{\frac {\pi }{2}}],x\longmapsto \arcsin x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e269068b1687b0c1f9ad4b5014b4e7cb54b611)
and is called
arcsine.
The
inverse function
of the real
cosine function
is
-
![{\displaystyle [-1,1]\longrightarrow [0,\pi ],x\longmapsto \arccos x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ecd68470a9279fb3e2ea542385322310d9b0f7f)
and is called
arccosine.
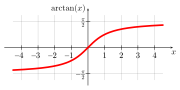Arkustangens
The
inverse function
of the real
tangent function
is
-
![{\displaystyle \mathbb {R} \longrightarrow ]-{\frac {\pi }{2}},{\frac {\pi }{2}}[,x\longmapsto \arctan x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a599a936531a4aaefac1af5be86d23f98e145ce7)
and is called
arctangent.
The
inverse function
of the real
cotangent function
is
-
![{\displaystyle \mathbb {R} \longrightarrow ]0,\pi [,x\longmapsto \operatorname {arccot} x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6f643c1b07952f1bae062cf8e79a6d782e9011f)
and is called
arccotangent.
For example, for the arctangent, we have, due to
fact,
