Template:Physeq1/MomentOfInertia

Description	Figure	Moment(s) of inertia
Point mass m at a distance r from the axis of rotation.		$I=mr^{2}$
Two point masses, M and m, with reduced mass $\mu$ and separated by a distance, x.		$I={\frac {Mm}{M\!+\!m}}x^{2}=\mu x^{2}$
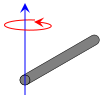
Rod of length L and mass m (Axis of rotation at the end of the rod)		$I_{\mathrm {end} }={\frac {mL^{2}}{3}}\,\!$
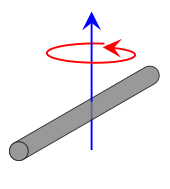
Rod of length L and mass m		$I_{\mathrm {center} }={\frac {mL^{2}}{12}}\,\!$
Thin circular hoop of radius r and mass m		$I_{z}=mr^{2}\!$ $I_{x}=I_{y}={\frac {mr^{2}}{2}}\,\!$
Thin cylindrical shell with open ends, of radius r and mass m		$I=mr^{2}\,\!$
Solid cylinder of radius r, height h and mass m		$I_{z}={\frac {mr^{2}}{2}}\,\!$ $I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)$
Sphere (hollow) of radius r and mass m		$I={\frac {2mr^{2}}{3}}\,\!$
Ball (solid) of radius r and mass m		$I={\frac {2mr^{2}}{5}}\,\!$
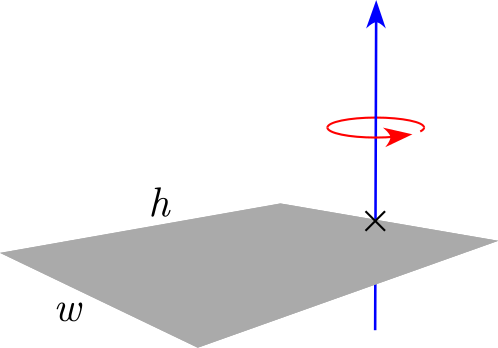
Thin rectangular plate of height h and of width w and mass m (Axis of rotation at the end of the plate)		$I_{e}={\frac {mh^{2}}{3}}+{\frac {mw^{2}}{12}}\,\!$
Solid cuboid of height h, width w, and depth d, and mass m		$I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)$ $I_{w}={\frac {1}{12}}m\left(h^{2}+d^{2}\right)$ $I_{d}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)$