Syllogisms
Jump to navigation
Jump to search
This page illustrates syllogisms in three different ways:
- With Venn diagrams, that show in which intersections of the three sets objects do not (black), can (white) or do (red) exist.
- With Euler diagrams, which are like Venn diagrams with empty regions removed. (Only small diagrams on top of the table.)
- The gist of this page is the reduction of this first-order logic topic to zeroth-order logic using binary square matrices that are essentially 8-ary logical connectives. There are 8 intersections of the three sets, and each intersection can either contain elements or not. So there are 28 = 256 situations that can be the case. Each statement (premise or conclusion) can be denoted by the set of situations in which it is true.
All Syllogisms (table of contents)[edit | edit source]
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
|
.svg)
| |
| 1 |  Barbara |
 Barbari |
 Darii |
 Ferio |
 Celaront |
 Celarent |
||||||||
| 2 |  Festino |
 Cesaro |
 Cesare |
 Camestres |
 Camestros |
 Baroco |
||||||||
| 3 |  Darapti |
 Datisi |
 Disamis |
 Felapton |
 Ferison |
 Bocardo | ||||||||
| 4 |  Bamalip |
 Dimatis |
 Fesapo |
 Fresison |
 Calemes |
 Calemos |
Graphical elements[edit | edit source]
 |
 Light vertices indicate that an area is empty, dark vertices indicate that there is at least one element. |
Examples[edit | edit source]
Barbara (AAA-1)[edit | edit source]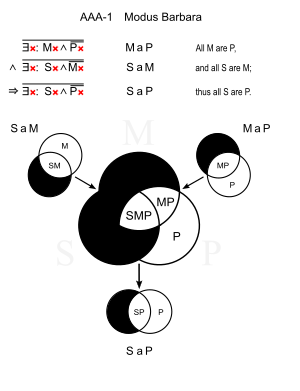
|
 |
Celarent (EAE-1)[edit | edit source]
|
 |
Similar: Cesare (EAE-2)
| Calemes (AEE-4) |
|---|
|
Calemes is like Celarent with S and P exchanged. |
Darii (AII-1)[edit | edit source]
|
 |
Similar: Datisi (AII-3)
| Dimatis (IAI-4) |
|---|
|
Dimatis is like Darii with S and P exchanged. |
Ferio (EIO-1)[edit | edit source]
|
 |
Similar: Festino (EIO-2), Ferison (EIO-3), Fresison (EIO-4)
Baroco (AOO-2)[edit | edit source]
|
 |
Bocardo (OAO-3)[edit | edit source]
|
 |
Barbari (AAI-1) [edit | edit source]
| Bamalip (AAI-4) |
|---|
|
Bamalip is like Barbari with S and P exchanged: |
Celaront (EAO-1)[edit | edit source]
Similar: Cesaro (EAO-2)
Camestros (AEO-2)[edit | edit source]
Similar: Calemos (AEO-4)
Felapton (EAO-3)[edit | edit source]
|
 |
Similar: Fesapo (EAO-4)
Darapti (AAI-3)[edit | edit source]
|
 |
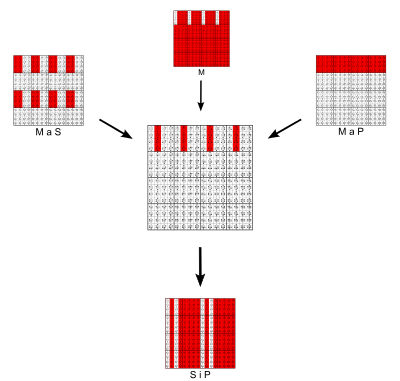