Jump to content

Studies of Euler diagrams/dukeli NP/ordered

Add links
From Wikiversity

dummy


This matrix is essentially like that shown in keyneg, but with rows and columns reordered.
In this arrangement all functions in the same N-EC are in the same double column,
and all functions in the same P-EC are in the same (double) row.
Pairs of mirror symmetric Euler diagrams are in the same table cell.   (In big cells with four diagrams they are in opposite corners.)

This is a essentially a detailed version of this table. See NP tables.

The indices of this table refer to the function dukeli. But the sequence of the columns is based on the Boolean functions' Zhegalkin indices.
These numbers have a mouseover with two lines: Above the little-endian binary expression of the Zhegalkin index, and below the truth table of the Boolean function.

The rows can be ordered in four different ways:

  • by binary weight of the Zhegalkin indices   (5, 5,  6, 6, 6,  7, 7, 7,  8, 8)
  • by number of different functions   (4 rows with 12, 6 double rows with 24)
  • by smallest Zhegalkin index of the row
  • by number of negators in the transformation from dukeli
W C
2290
2291
8398
8399
11278
11279
16558
16559
18958
18959
25138
25139
6 24 2290 2

2290
(~0, 3, ~2, 1)
3972
(~1, 2, ~3, 0)

3972
(0, ~3, 2, ~1)
2290
(1, ~2, 3, ~0)

3970
(~0, 2, ~3, 1)
2292
(~1, 3, ~2, 0)

2292
(0, ~2, 3, ~1)
3970
(1, ~3, 2, ~0)

8398
(~0, 3, ~1, 2)
13200
(~2, 1, ~3, 0)

13200
(0, ~3, 1, ~2)
8398
(2, ~1, 3, ~0)

13186
(~0, 1, ~3, 2)
8412
(~2, 3, ~1, 0)

8412
(0, ~1, 3, ~2)
13186
(2, ~3, 1, ~0)

11278
(~0, 2, ~1, 3)
14640
(~3, 1, ~2, 0)

14640
(0, ~2, 1, ~3)
11278
(3, ~1, 2, ~0)

14386
(~0, 1, ~2, 3)
11532
(~3, 2, ~1, 0)

11532
(0, ~1, 2, ~3)
14386
(3, ~2, 1, ~0)

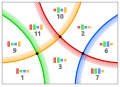
16558
(~1, 3, ~0, 2)
21904
(~2, 0, ~3, 1)

21904
(1, ~3, 0, ~2)
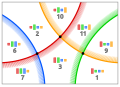
16558
(2, ~0, 3, ~1)

21892
(~1, 0, ~3, 2)
16570
(~2, 3, ~0, 1)

16570
(1, ~0, 3, ~2)
21892
(2, ~3, 0, ~1)

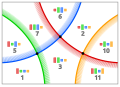
18958
(~1, 2, ~0, 3)
22864
(~3, 0, ~2, 1)

22864
(1, ~2, 0, ~3)
18958
(3, ~0, 2, ~1)

22612
(~1, 0, ~2, 3)
19210
(~3, 2, ~0, 1)

19210
(1, ~0, 2, ~3)
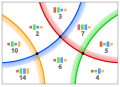
22612
(3, ~2, 0, ~1)

25138
(~2, 1, ~0, 3)
25924
(~3, 0, ~1, 2)

25924
(2, ~1, 0, ~3)
25138
(3, ~0, 1, ~2)

25684
(~2, 0, ~1, 3)
25378
(~3, 1, ~0, 2)

25378
(2, ~0, 1, ~3)
25684
(3, ~1, 0, ~2)
7 24 2291 2

2293
(~0, ~3, 2, 1)
3971
(~1, ~2, 3, 0)

3971
(0, 3, ~2, ~1)
2293
(1, 2, ~3, ~0)

3973
(~0, ~2, 3, 1)
2291
(~1, ~3, 2, 0)

2291
(0, 2, ~3, ~1)
3973
(1, 3, ~2, ~0)

8413
(~0, ~3, 1, 2)
13187
(~2, ~1, 3, 0)

13187
(0, 3, ~1, ~2)
8413
(2, 1, ~3, ~0)

13201
(~0, ~1, 3, 2)
8399
(~2, ~3, 1, 0)

8399
(0, 1, ~3, ~2)
13201
(2, 3, ~1, ~0)

11533
(~0, ~2, 1, 3)
14387
(~3, ~1, 2, 0)

14387
(0, 2, ~1, ~3)
11533
(3, 1, ~2, ~0)

14641
(~0, ~1, 2, 3)
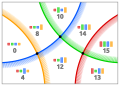
11279
(~3, ~2, 1, 0)

11279
(0, 1, ~2, ~3)
14641
(3, 2, ~1, ~0)

16571
(~1, ~3, 0, 2)
21893
(~2, ~0, 3, 1)

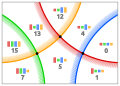
21893
(1, 3, ~0, ~2)
16571
(2, 0, ~3, ~1)

21905
(~1, ~0, 3, 2)
16559
(~2, ~3, 0, 1)

16559
(1, 0, ~3, ~2)
21905
(2, 3, ~0, ~1)

19211
(~1, ~2, 0, 3)
22613
(~3, ~0, 2, 1)

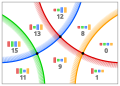
22613
(1, 2, ~0, ~3)
19211
(3, 0, ~2, ~1)

22865
(~1, ~0, 2, 3)
18959
(~3, ~2, 0, 1)

18959
(1, 0, ~2, ~3)
22865
(3, 2, ~0, ~1)

25379
(~2, ~1, 0, 3)
25685
(~3, ~0, 1, 2)

25685
(2, 1, ~0, ~3)
25379
(3, 0, ~1, ~2)

25925
(~2, ~0, 1, 3)
25139
(~3, ~1, 0, 2)

25139
(2, 0, ~1, ~3)
25925
(3, 1, ~0, ~2)
7 24 2298 3

2298
(~0, ~3, ~2, 1)
3980
(~1, ~2, ~3, 0)

3980
(0, ~3, ~2, ~1)
2298
(1, ~2, ~3, ~0)

3978
(~0, ~2, ~3, 1)
2300
(~1, ~3, ~2, 0)

2300
(0, ~2, ~3, ~1)
3978
(1, ~3, ~2, ~0)

8430
(~0, ~3, ~1, 2)
13232
(~2, ~1, ~3, 0)

13232
(0, ~3, ~1, ~2)
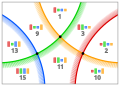
8430
(2, ~1, ~3, ~0)

13218
(~0, ~1, ~3, 2)
8444
(~2, ~3, ~1, 0)

8444
(0, ~1, ~3, ~2)
13218
(2, ~3, ~1, ~0)

11790
(~0, ~2, ~1, 3)
15152
(~3, ~1, ~2, 0)

15152
(0, ~2, ~1, ~3)
11790
(3, ~1, ~2, ~0)

14898
(~0, ~1, ~2, 3)
12044
(~3, ~2, ~1, 0)

12044
(0, ~1, ~2, ~3)
14898
(3, ~2, ~1, ~0)

16622
(~1, ~3, ~0, 2)
21968
(~2, ~0, ~3, 1)

21968
(1, ~3, ~0, ~2)
16622
(2, ~0, ~3, ~1)

21956
(~1, ~0, ~3, 2)
16634
(~2, ~3, ~0, 1)

16634
(1, ~0, ~3, ~2)
21956
(2, ~3, ~0, ~1)

19982
(~1, ~2, ~0, 3)
23888
(~3, ~0, ~2, 1)

23888
(1, ~2, ~0, ~3)
19982
(3, ~0, ~2, ~1)

23636
(~1, ~0, ~2, 3)
20234
(~3, ~2, ~0, 1)

20234
(1, ~0, ~2, ~3)
23636
(3, ~2, ~0, ~1)

29234
(~2, ~1, ~0, 3)
30020
(~3, ~0, ~1, 2)

30020
(2, ~1, ~0, ~3)
29234
(3, ~0, ~1, ~2)

29780
(~2, ~0, ~1, 3)
29474
(~3, ~1, ~0, 2)

29474
(2, ~0, ~1, ~3)
29780
(3, ~1, ~0, ~2)
8 24 2299 1

2301
(~0, 3, 2, 1)
3979
(~1, 2, 3, 0)

3979
(0, 3, 2, ~1)
2301
(1, 2, 3, ~0)

3981
(~0, 2, 3, 1)
2299
(~1, 3, 2, 0)

2299
(0, 2, 3, ~1)
3981
(1, 3, 2, ~0)

8445
(~0, 3, 1, 2)
13219
(~2, 1, 3, 0)

13219
(0, 3, 1, ~2)
8445
(2, 1, 3, ~0)

13233
(~0, 1, 3, 2)
8431
(~2, 3, 1, 0)

8431
(0, 1, 3, ~2)
13233
(2, 3, 1, ~0)

12045
(~0, 2, 1, 3)
14899
(~3, 1, 2, 0)

14899
(0, 2, 1, ~3)
12045
(3, 1, 2, ~0)

15153
(~0, 1, 2, 3)
11791
(~3, 2, 1, 0)

11791
(0, 1, 2, ~3)
15153
(3, 2, 1, ~0)

16635
(~1, 3, 0, 2)
21957
(~2, 0, 3, 1)

21957
(1, 3, 0, ~2)
16635
(2, 0, 3, ~1)

21969
(~1, 0, 3, 2)
16623
(~2, 3, 0, 1)

16623
(1, 0, 3, ~2)
21969
(2, 3, 0, ~1)

20235
(~1, 2, 0, 3)
23637
(~3, 0, 2, 1)

23637
(1, 2, 0, ~3)
20235
(3, 0, 2, ~1)

23889
(~1, 0, 2, 3)
19983
(~3, 2, 0, 1)

19983
(1, 0, 2, ~3)
23889
(3, 2, 0, ~1)

29475
(~2, 1, 0, 3)
29781
(~3, 0, 1, 2)

29781
(2, 1, 0, ~3)
29475
(3, 0, 1, ~2)

30021
(~2, 0, 1, 3)
29235
(~3, 1, 0, 2)

29235
(2, 0, 1, ~3)
30021
(3, 1, 0, ~2)
5 24 2754 3

2756
(~0, ~3, 2, ~1)
2754
(~1, ~2, 3, ~0)

2754
(~0, 3, ~2, ~1)
2756
(~1, 2, ~3, ~0)

3236
(~0, ~2, 3, ~1)
3234
(~1, ~3, 2, ~0)

3234
(~0, 2, ~3, ~1)
3236
(~1, 3, ~2, ~0)

8912
(~0, ~3, 1, ~2)
8898
(~2, ~1, 3, ~0)

8898
(~0, 3, ~1, ~2)
8912
(~2, 1, ~3, ~0)

12440
(~0, ~1, 3, ~2)
12426
(~2, ~3, 1, ~0)

12426
(~0, 1, ~3, ~2)
12440
(~2, 3, ~1, ~0)

11552
(~0, ~2, 1, ~3)
11298
(~3, ~1, 2, ~0)

11298
(~0, 2, ~1, ~3)
11552
(~3, 1, ~2, ~0)

14600
(~0, ~1, 2, ~3)
14346
(~3, ~2, 1, ~0)

14346
(~0, 1, ~2, ~3)
14600
(~3, 2, ~1, ~0)

17584
(~1, ~3, 0, ~2)
17572
(~2, ~0, 3, ~1)

17572
(~1, 3, ~0, ~2)
17584
(~2, 0, ~3, ~1)

20632
(~1, ~0, 3, ~2)
20620
(~2, ~3, 0, ~1)

20620
(~1, 0, ~3, ~2)
20632
(~2, 3, ~0, ~1)

19264
(~1, ~2, 0, ~3)
19012
(~3, ~0, 2, ~1)

19012
(~1, 2, ~0, ~3)
19264
(~3, 0, ~2, ~1)

22792
(~1, ~0, 2, ~3)
22540
(~3, ~2, 0, ~1)

22540
(~1, 0, ~2, ~3)
22792
(~3, 2, ~0, ~1)

25408
(~2, ~1, 0, ~3)
25168
(~3, ~0, 1, ~2)

25168
(~2, 1, ~0, ~3)
25408
(~3, 0, ~1, ~2)

25888
(~2, ~0, 1, ~3)
25648
(~3, ~1, 0, ~2)

25648
(~2, 0, ~1, ~3)
25888
(~3, 1, ~0, ~2)
6 24 2755 1

3237
(0, ~3, 2, 1)
3235
(1, ~2, 3, 0)

3235
(0, 3, ~2, 1)
3237
(1, 2, ~3, 0)

2757
(0, ~2, 3, 1)
2755
(1, ~3, 2, 0)

2755
(0, 2, ~3, 1)
2757
(1, 3, ~2, 0)

12441
(0, ~3, 1, 2)
12427
(2, ~1, 3, 0)

12427
(0, 3, ~1, 2)
12441
(2, 1, ~3, 0)

8913
(0, ~1, 3, 2)
8899
(2, ~3, 1, 0)

8899
(0, 1, ~3, 2)
8913
(2, 3, ~1, 0)

14601
(0, ~2, 1, 3)
14347
(3, ~1, 2, 0)

14347
(0, 2, ~1, 3)
14601
(3, 1, ~2, 0)

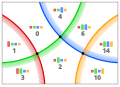
11553
(0, ~1, 2, 3)
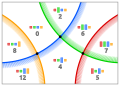
11299
(3, ~2, 1, 0)

11299
(0, 1, ~2, 3)
11553
(3, 2, ~1, 0)

20633
(1, ~3, 0, 2)
20621
(2, ~0, 3, 1)

20621
(1, 3, ~0, 2)
20633
(2, 0, ~3, 1)

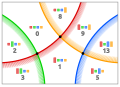
17585
(1, ~0, 3, 2)
17573
(2, ~3, 0, 1)

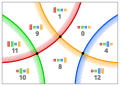
17573
(1, 0, ~3, 2)
17585
(2, 3, ~0, 1)

22793
(1, ~2, 0, 3)
22541
(3, ~0, 2, 1)

22541
(1, 2, ~0, 3)
22793
(3, 0, ~2, 1)

19265
(1, ~0, 2, 3)
19013
(3, ~2, 0, 1)

19013
(1, 0, ~2, 3)
19265
(3, 2, ~0, 1)

25889
(2, ~1, 0, 3)
25649
(3, ~0, 1, 2)

25649
(2, 1, ~0, 3)
25889
(3, 0, ~1, 2)

25409
(2, ~0, 1, 3)
25169
(3, ~1, 0, 2)

25169
(2, 0, ~1, 3)
25409
(3, 1, ~0, 2)
5 12 2760 4

2760
(~0, ~3, ~2, ~1)
2760
(~1, ~2, ~3, ~0)

3240
(~0, ~2, ~3, ~1)
3240
(~1, ~3, ~2, ~0)

8928
(~0, ~3, ~1, ~2)
8928
(~2, ~1, ~3, ~0)

12456
(~0, ~1, ~3, ~2)
12456
(~2, ~3, ~1, ~0)

11808
(~0, ~2, ~1, ~3)
11808
(~3, ~1, ~2, ~0)

14856
(~0, ~1, ~2, ~3)
14856
(~3, ~2, ~1, ~0)

17632
(~1, ~3, ~0, ~2)
17632
(~2, ~0, ~3, ~1)

20680
(~1, ~0, ~3, ~2)
20680
(~2, ~3, ~0, ~1)

20032
(~1, ~2, ~0, ~3)
20032
(~3, ~0, ~2, ~1)

23560
(~1, ~0, ~2, ~3)
23560
(~3, ~2, ~0, ~1)

29248
(~2, ~1, ~0, ~3)
29248
(~3, ~0, ~1, ~2)

29728
(~2, ~0, ~1, ~3)
29728
(~3, ~1, ~0, ~2)
6 12 2761 0

3241
(0, 3, 2, 1)
3241
(1, 2, 3, 0)

2761
(0, 2, 3, 1)
2761
(1, 3, 2, 0)

12457
(0, 3, 1, 2)
12457
(2, 1, 3, 0)

8929
(0, 1, 3, 2)
8929
(2, 3, 1, 0)

14857
(0, 2, 1, 3)
14857
(3, 1, 2, 0)

11809
(0, 1, 2, 3)
11809
(3, 2, 1, 0)

20681
(1, 3, 0, 2)
20681
(2, 0, 3, 1)

17633
(1, 0, 3, 2)
17633
(2, 3, 0, 1)

23561
(1, 2, 0, 3)
23561
(3, 0, 2, 1)

20033
(1, 0, 2, 3)
20033
(3, 2, 0, 1)

29729
(2, 1, 0, 3)
29729
(3, 0, 1, 2)

29249
(2, 0, 1, 3)
29249
(3, 1, 0, 2)
7 12 2766 2

2766
(~0, 3, 2, ~1)
2766
(~1, 2, 3, ~0)

3246
(~0, 2, 3, ~1)
3246
(~1, 3, 2, ~0)

8946
(~0, 3, 1, ~2)
8946
(~2, 1, 3, ~0)

12474
(~0, 1, 3, ~2)
12474
(~2, 3, 1, ~0)

12066
(~0, 2, 1, ~3)
12066
(~3, 1, 2, ~0)

15114
(~0, 1, 2, ~3)
15114
(~3, 2, 1, ~0)

17652
(~1, 3, 0, ~2)
17652
(~2, 0, 3, ~1)

20700
(~1, 0, 3, ~2)
20700
(~2, 3, 0, ~1)

20292
(~1, 2, 0, ~3)
20292
(~3, 0, 2, ~1)

23820
(~1, 0, 2, ~3)
23820
(~3, 2, 0, ~1)

29520
(~2, 1, 0, ~3)
29520
(~3, 0, 1, ~2)

30000
(~2, 0, 1, ~3)
30000
(~3, 1, 0, ~2)
8 12 2767 2

3247
(0, ~3, ~2, 1)
3247
(1, ~2, ~3, 0)

2767
(0, ~2, ~3, 1)
2767
(1, ~3, ~2, 0)

12475
(0, ~3, ~1, 2)
12475
(2, ~1, ~3, 0)

8947
(0, ~1, ~3, 2)
8947
(2, ~3, ~1, 0)

15115
(0, ~2, ~1, 3)
15115
(3, ~1, ~2, 0)

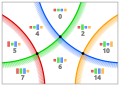
12067
(0, ~1, ~2, 3)
12067
(3, ~2, ~1, 0)

20701
(1, ~3, ~0, 2)
20701
(2, ~0, ~3, 1)

17653
(1, ~0, ~3, 2)
17653
(2, ~3, ~0, 1)

23821
(1, ~2, ~0, 3)
23821
(3, ~0, ~2, 1)

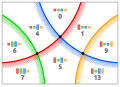
20293
(1, ~0, ~2, 3)
20293
(3, ~2, ~0, 1)

30001
(2, ~1, ~0, 3)
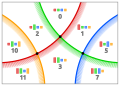
30001
(3, ~0, ~1, 2)

29521
(2, ~0, ~1, 3)
29521
(3, ~1, ~0, 2)
Retrieved from "https://en.wikiversity.org/w/index.php?title=Studies_of_Euler_diagrams/dukeli_NP/ordered&oldid=2474232"