Theory of relativity/Special relativity/spacetime diagrams and vectors

Physics

Special relativity

Subject classification: this is a mathematics resource.

Subject classification: this is a physics resource.

Educational level: this is a secondary education resource.

Educational level: this is a tertiary (university) resource.

This article presumes that the reader has read the earlier articles in this series, particularly Special relativity/space, time, and the Lorentz transform. This article may be more complicated than the preceding ones in the series.

When dealing with relativity, a useful concept is that of spacetime, a sort of 4-dimensional diagram on which events occur. An event is something that happens at a specific place at a specific time, such as the explosion of the Crab Nebula, Queen Elizabeth's coronation, or the light pulse hitting the detector in Mike and Leslie's first experiment in Special relativity/space, time, and the Lorentz transform.

In any situation in which measurements are made, it is important to distinguish between the event itself and the various coordinates that various observers might assign to it. The reader is already familiar with the concept of different coordinate systems for space—Cartesian, cylindrical, spherical, etc. These are just different ways of assigning triples of numbers to points in space. The points are the same; the coordinates are simply different in different coordinate systems.

The same principle applies when analyzing events in different, perhaps moving, frames of reference. Different observers can assign different coordinates (x, y, z, t) to the same event. Because of relativity and the Lorentz transform, we have to include time in the list of coordinates; it is no longer true that everyone agrees on the time at which an event took place. When two frames of reference are in uniform motion relative to each other, the functions relating their coordinate systems are the Galilean transform if relativity is not being taken into account, and the Lorentz transform if it is.

The experiment of Mike and Leslie

Figure 1: Events A, B, and C in Mike's frame of reference.

We can plot Mike and Leslie's first experiment (see Special relativity/space, time, and the Lorentz transform) on a spacetime diagram. Since there is no 4-dimensional paper or 4-dimensional computer screens, it is common to omit two space coordinates, and show only time and one space coordinate, such as x and t. By convention, t runs vertically upward. Figure 1 shows the events A, B, and C in Mike's frame of reference.

Event A, light is emitted: x' = 0, y' = 0, t' = 0

Event B, light hits the mirror and is reflected: x' = 0, y' = 4, t' = 4

Event C, light reaches the detector: x' = 0, y' = 0, t' = 8

Unfortunately, we can't show the y coordinate. One could imagine the y coordinate coming out of the computer screen, so that event B is in front of events A or C. But it doesn't matter. The x and t coordinates are the only ones that are important.

Figure 2: Both Mike's (light colors, x' and t') and Leslie's (dark colors, x and t) coordinate systems displayed on the same spacetime diagram. The yellow dotted lines are the "light cone" lines, explained later.

Figure 2 shows both coordinate systems on the same spacetime diagram. Mike's coordinates are x' and t', and the lines of constant x' are light red and vertical, counting from left to right. Mike's lines of constant t' are light blue and horizontal, counting from bottom to top. Leslie's coordinates are x and t, and the lines of constant x are dark red and slanted from vertical, counting from left to right. Leslie's lines of constant t are dark blue and slanted from horizontal, counting from bottom to top. In all cases the calibration is in seconds or light-seconds. Red lines, light or dark, are lines of constant x, and blue lines, light or dark, are lines of constant time.

The reader can check that event C has coordinates in the two systems of

(Mike's system) x' = 0, t' = 8

(Leslie's system) x = 6, t = 10

and that in fact the Lorentz transform is satisfied everywhere, with c = 1.0 (we are calibrating in seconds and light-seconds, so we can do this), and v = 0.6:

$t={\frac {t'+vx'/c^{2}}{\sqrt {1-v^{2}/c^{2}}}}=1.25(t'+0.6x')$

$x={\frac {x'+vt'}{\sqrt {1-v^{2}/c^{2}}}}=1.25(x'+0.6t')$

$t'={\frac {t-vx/c^{2}}{\sqrt {1-v^{2}/c^{2}}}}=1.25(t-0.6x)$

$x'={\frac {x-vt}{\sqrt {1-v^{2}/c^{2}}}}=1.25(x-0.6t)$

For example, the point indicated by the green dot in the lower-left part of the figure has coordinates

x' = -9, t' = -5

x = -15, t = -13

This is what Lorentz transforms look like. When a frame of reference moves, its lines of constant x tilt away from vertical in one direction (counterclockwise in this instance), while the lines of constant t tilt away from horizontal in the other direction. They both tilt toward the light cone—more about that later.

Figure 3: An ordinary Euclidean transform is much simpler.

Ordinary Euclidean transformations are much simpler, as shown in Figure 3. The coordinate axes simply rotate.

Figure 4: Leslie's unskewed view of things.

Leslie doesn't believe in the skewed depiction of her coordinate system in Figure 2. She considers her (x, t) coordinate lines to be perfectly vertical and horizontal, as shown in figure 4. In her system, events A, B, and C are not stacked on top of each other; they happen at different x coordinates, because Mike's experimental apparatus is moving to the right.

World lines

The position of any object, graphed on a spacetime diagram, is called its world line. In any diagram with the time axis going straight up, the world line of a stationary object is vertical. The world lines of moving objects lean over to the left or right. In Figure 2, Mike's world line is the light red vertical line at x' = 0. Leslie's world line is the dark red somewhat vertical line at x = 0. Both lines pass through event A, since Mike and Leslie are both present at event A. In figure 4, Mike's world line would be slanted and passing through events A, B, and C, since Mike is present at all three events. Leslie's world line is of course directly vertical at x=0. Leslie's assistant Kate has a world line that is directly vertical (Leslie and Kate are not moving relative to each other), at x=6. Kate's world line passes through event C. Recall that Kate was posted at that position so that she would see event C directly.

If an object changes its speed of motion, its world line will have bends in it. In fact, for arbitrary motion, the world line can be curved, but that gets into general relativity, which is beyond the scope of this article.

The light cone

Figure 5: Perspective view of a light cone, with two spatial dimensions plus the time dimension.

In our 2-dimensional diagrams, the locus of spacetime points with x² = (ct)² is called the light cone. Taking the square root of both sides, we have x = ± ct. The light cones are indicated in Figure 2 by dashed yellow lines. They are clearly the events that would be reached from the origin by something traveling at the speed of light. In the full 4 dimensions, the light cone is the locus of points with

(x² + y² + z²) = (c t)²

These are clearly the events reachable from the origin by something traveling at the speed of light.

Figure 5 shows a perspective view of a light cone with two spatial dimensions plus the time dimension, and shows why it is called a "cone". A is the origin. B is inside the cone, so something traveling at less than the speed of light could reach B from A. C is outside the cone. It cannot be reached from A by anything traveling at less than the speed of light. The top part is called the "forward light cone", and consists of those events that one could reach. The bottom part is the "backward light cone", and consists of those events that one could be reached by, or, equivalently, events that one could have seen or known about.

Figure 6: A slightly relativistic Lorentz transform, v=0.1 c.

Figure 7: A very relativistic Lorentz transform, v=0.9 c.

In a Lorentz transform, the lines of constant t, and the lines of constant x, lean toward the light cone. They never reach it. (This will be a consequence of the fundamental theorem, derived below.) Figure 2 showed a moderately relativistic (v = 0.6 c) situation, so the lines leaned moderately far. Figure 6 shows a transform that is only slightly relativistic (v = 0.1 c), and Figure 7 shows one that is extremely relativistic (v = 0.9 c).

The fundamental theorem

An extremely important theorem is this:

The value of $c^{2}t^{2}-x^{2}\,$ is preserved under the Lorentz transformation.

Proof:

$c^{2}t^{2}-x^{2}={\frac {c^{2}(t'+vx'/c^{2})^{2}}{1-v^{2}/c^{2}}}-{\frac {(x'+vt')^{2}}{1-v^{2}/c^{2}}}$

$\ \ ={\frac {c^{2}t'^{2}+v^{2}x'^{2}/c^{2}+2t'vx'-x'^{2}-v^{2}t'^{2}-2x'vt'}{1-v^{2}/c^{2}}}$

$\ \ ={\frac {c^{2}t'^{2}+v^{2}x'^{2}/c^{2}-x'^{2}-v^{2}t'^{2}}{1-v^{2}/c^{2}}}$

$\ \ ={\frac {c^{2}t'^{2}-x'^{2}-(v^{2}/c^{2})(c^{2}t'^{2}-x'^{2})}{1-v^{2}/c^{2}}}$

$\ \ =c^{2}t'^{2}-x'^{2}$      Q.E.D.

When we take the y and z coordinates into account, the theorem is actually:

The value of $c^{2}t^{2}-x^{2}-y^{2}-z^{2}\,$ is preserved under the Lorentz transformation.

Intervals and vectors

We have been glossing over an important point, by assuming that all coordinate systems have their origin (x=y=z=t=0) at the same event. This of course isn't true; coordinate transformations can add constant offsets to any coordinates. In fact the same phenomenon is at work in ordinary Euclidean geometry. A Euclidean transform is a combination of rotations and translations. In spacetime physics there can be translations in any of the spatial coordinates or in the time coordinate.

So the Lorentz transform equations actually look like

$t={\frac {t'+vx'/c^{2}}{\sqrt {1-v^{2}/c^{2}}}}+K$

where the K's are constant offsets that need to be worked out in each case.

The fundamental theorem is actually about intervals, or spacetime vectors. Given two events, let Δx be the distance between them along the x axis, similarly for Δy, Δz, and Δt. The fundamental theorem relates to these differences between the coordinates:

The value of $c^{2}(\Delta {}t)^{2}-(\Delta {}x)^{2}-(\Delta {}y)^{2}-(\Delta {}z)^{2}\,$ is preserved under the Lorentz transformation.

In fact, all of relativity and mechanics relates to differences between events. Exactly where a given observer's "origin" is is of no significance.

The quantities Δx, Δy, Δz, and Δt are the components of the vector from one point to another. What the fundamental theorem actually says is that all observers, in all states of motion, agree on the quantity $c^{2}(\Delta {}t)^{2}-(\Delta {}x)^{2}-(\Delta {}y)^{2}-(\Delta {}z)^{2}\,$, in whatever their own coordinate system is, for the vector from one event to another. This quantity is called the squared length of the vector. It's also called the metric of the vector.

Now the length of a vector in ordinary 3-dimensional Euclidean space is

${\sqrt {(\Delta {}x)^{2}+(\Delta {}y)^{2}+(\Delta {}z)^{2}}}$

Why don't we just take the square root, and call that the "length" of the spacetime vector, the way we do in the Euclidean case? It's because the "squared length" might be negative. The best we can do is calculate this "squared length", and then take the square root of that, or of its negative, depending on the circumstances, if it is useful to do so.

The "spacelike" and "timelike" metric conventions

Some people define the metric as

$c^{2}(\Delta {}t)^{2}-(\Delta {}x)^{2}-(\Delta {}y)^{2}-(\Delta {}z)^{2}\,$

and some define it as

$(\Delta {}x)^{2}+(\Delta {}y)^{2}+(\Delta {}z)^{2}-c^{2}(\Delta {}t)^{2}\,$

The former is called the "timelike convention", and is what we are using. The latter is the "spacelike convention". There are arguments that can be made for either convention. The "spacelike convention" caters to intervals between spatially separated things, and allows one to take the square root of the "squared length" to get the distance between those things. The "timelike convention" allows one to track something that is moving slower than the speed of light, and find out how much time will elapse, on that observer's own clock, between the two events.

The controversy has raged for 100 years.

Time-like, space-like, and light-like vectors

The important point from the fundamental theorem is that all observers, in all frames of reference, agree on the squared length, that is, the metric, of the vector between any two events. (This is analogous to the theorem from ordinary geometry, that all Cartesian coordinate systems give the same value for the length of the vector between two points. That theorem follows from the theorem of Pythagoras.)

If the metric of a vector is positive, that is:

$c^{2}(\Delta {}t)^{2}>(\Delta {}x)^{2}+(\Delta {}y)^{2}+(\Delta {}z)^{2}\,$

that vector is said to be time-like.

If the metric is negative, that is:

$c^{2}(\Delta {}t)^{2}<(\Delta {}x)^{2}+(\Delta {}y)^{2}+(\Delta {}z)^{2}\,$

that vector is said to be space-like.

If the metric is zero, that is:

$c^{2}(\Delta {}t)^{2}=(\Delta {}x)^{2}+(\Delta {}y)^{2}+(\Delta {}z)^{2}\,$

that vector is said to be light-like or to be a null vector.

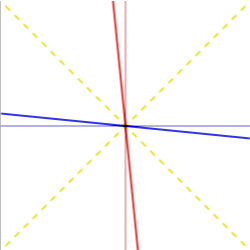
A light-like vector is parallel to a light cone. A time-like vector is more nearly vertical, since its value of $|\Delta {}t|\,$ is greater. A space-like vector is more nearly horizontal, since its value of $|\Delta {}x|\,$ is greater. Figure 8 shows some of the three kinds of vectors.

Figure 8: Some vectors: light-like, time-like, and space-like.

${\vec {AB}}$ is light-like.

${\vec {CD}}$ is time-like.

${\vec {EF}}$ is space-like.

In any frame of reference, the lines of constant x are time-like, since Δx = 0. The lines of constant t are space-like, since Δt = 0. Since all observers agree on a vector's metric, they all agree on whether it is time-like, space-like, or light-like. It follows from this that, in a Lorentz transform such as those shown in Figures 2, 6, and 7, the transformed axes lean toward a light cone but never reach it. Also, the light cones themselves, are unchanged.

Metrics are calculated with a sort of Pythagorean law, except that the squares of the two sides of the triangle are subtracted instead of being added.

Proper time, and the "Twin Paradox"

Figure 9: A spacetime diagram showing the Twin Paradox. The journey starts at A, turns around at B, and ends at C. Appropriate parts of light cones are shown. Calibration is years and light-years. Line slopes have been fudged somewhat for clarity.

The elapsed time that will be measured on any observer's own clock as he or she proceeds from one event to another is just Δt in his or her coordinate system. Since Δx is zero in that system, the local elapsed time is just the metric. Since all observers agree on the metric, any observer can calculate the readings of anyone else's clock, as long as that person traveled uniformly from one event to the other.

The "Twin Paradox" is a famous conundrum in which one twin gets into a relativistic rocket at an early age, and flies to some distant star and back, while the other twin stays on Earth. When she returns, she has not aged as much as her Earthbound twin.

This is easy to analyze in terms of spacetime vectors, as shown in Figure 9. Suppose the two trips go at a speed of (29/30) c, to Delta Eridani, 29 light years away. The Earthbound twin measures the trips as taking 30 years each way, for a total of 60 years. But the metric distances are $||{\vec {AB}}||=||{\vec {BC}}||={\sqrt {30^{2}-29^{2}}}={\sqrt {59}}=7.68$ years each way. This is the traveling twin's proper time, measured on her own clock and calendar. She has aged only 15.36 years.

The non-relativistic limit and the Galilean transform

Figure 10: A spacetime diagram calibrated a little more reasonably. Height of the graph is 1 second, width is 0.2 light-second. Speed of the dark red frame is 0.1 light-second per second, or 0.1 c.

In all of the preceding examples, the graphs have been calibrated in units of seconds and light-seconds. This has put the light cones at a 45 degree angle. But if we calibrate the graphs in terms of humanly-reasonable units, they look very different. Figure 10 shows the beginnings of such a graph, though it is still not humanly-reasonable. Time is calibrated with the height of the graph equal to 1 second, and space is calibrated with the width of the graph equal to 0.2 light-seconds, which is still rather extreme. With this scaling, the speed of light is visually equal to 0.2. The t=0 and t'=0 lines (light blue and dark blue) are nearly indistinguishable, meaning that the two observers very nearly agree on the time. The light cone lines are also close to horizontal.

As we change the scaling to be even more reasonable on a human scale, say, meters and seconds, the effect is even more pronounced. The light blue and dark blue lines would essentially coincide. The x=0 line has the appropriate slope. This would be extremely close to the Galilean transform, which is the non-relativistic limit of the Lorentz transform.

See also

• Special relativity/space, time, and the Lorentz transform
• Special relativity/momentum
• Special relativity/energy
• Special relativity/E = mc²