Quantum mechanics/Timeline
Quantum mechanics timeline
[edit | edit source]- See also Wikipedia's Timeline of quantum mechanics
- More Wikiversity resources can be found on Quantum mechanics.
- This version contains calculations. For a slightly simpler discussion, see How_things_work_college_course/Quantum_mechanics_timeline
What is Quantum Mechanics and what is Old Quantum Mechanics?
[edit | edit source]
Quantum mechanics (QM – also known as quantum physics, or quantum theory) is a branch of physics which deals with physical phenomena at microscopic scales. It departs from classical mechanics primarily at the quantum realm of atomic and subatomic length scales. Quantum mechanics provides a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. In most contexts, the term 'Quantum Mechanics' does not refer to theories that incorporate Einstein's theories of Relativity. [1]
Old quantum theory is a collection of results from the years 1900–1925 which predate modern quantum mechanics. Although the theory was never complete or self-consistent, it yielded enough successes to establish that the classical Newtonian view of particle motion was insufficient. In 1926 Erwin Schrödinger found a completely quantum mechanical wave-equation, which reproduced all the successes of the old quantum theory without ambiguities and inconsistencies. [2] At approximately the same time a matrix version of the theory was developed, and eventually the two versions merged to become equivalent. This essay focuses on the more accessible wave version.[3]
When is a system in the quantum realm?
[edit | edit source]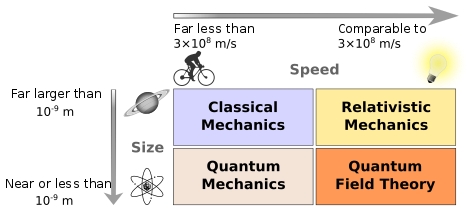
The Planck constant (denoted ) is a physical constant that appears throughout the theory of quantum mechanics, but that has no basis in the classical physics of Isaac Newton. The units of Plank's constant can be expressed as either, [energy]·[time], or as [mass]·[velocity]·[length]; (both are called action). A particle is likely to be in the quantum realm if either the mass, speed, or length is small:
- Electrons have less mass than protons or neutrons. For this reason, the electrons in an atom must be modeled by a quantum theory, but we have the option of treating the nucleus as a stationary and classical object at the center.[4]
- Electrons confined to a small space, such as the atom (typically 10-10 meters) will exhibit quantum effects.
- Atoms move very slowly when they are very cold. Quantum effects can occur at very low temperatures.[5]
Timeline
[edit | edit source](Extracted from Wikipedia[6])
- 1900 - Max Planck vaguely [7] and reluctantly [8] introduces what we now call the photon to accurately model the experimentally observed spectrum of Black body radiation.
- 1905 – Albert Einstein uses Max Planck's hypothesis to explain the photoelectric effect. [9]
- 1909 – Geoffrey Ingram Taylor shows that photons interfere with themselves even if only one photon is near the slits at any given time.[10]
- 1913 – Bohr used the Rydberg's (1888) formula to hypothesize the "Rutherford-Bohr atom".[11]
- 1923 – Arthur Compton showed that X-rays bounce off and eject electrons in much the same way that billiard balls collide.
- 1924 – Louis De Broglie extends wave-particle duality to particles (using relativistic arguments).
- 1926 – Erwin Schrödinger proposes his Schrödinger wave equation but does not at first understand exactly what the "wave" actually is.
- 1926 – Max Born successfully interpreted the "wave" as the probability amplitude, whose absolute square,|ψ|2, is equal to the probability density.
- 1927 - Davisson and Germer[12] diffract electrons off a nickel crystal.
- 1927 – Werner Heisenberg formulates the quantum uncertainty principle at about the same year that the Copenhagen interpretation is established.
- 1935 - Schrödinger introduces Schrödinger's cat thought experiment in response to the Copenhagen interpretation.
Black-body radiation 1900
[edit | edit source]
Old quantum theory came into existence in 1900 with a calculation by Max Planck that precisely matched the observed patterns of black-body radiation. He used the hypothesis that energy is radiated and absorbed in discrete "quanta" (or "energy elements"). In Planck's theory, the constant emerged as a relation between the energy () and the frequency () associated with the the interaction of light with the walls of the back body. This relation is called the Planck relation:
-
()
Planck (cautiously) insisted that this was simply an aspect of the processes of absorption and emission of radiation and had nothing to do with the physical reality of the radiation itself.[13] In fact, he considered his quantum hypothesis a mathematical trick to get the right answer rather than a sizeable discovery.

This equation predicts that photon energy is directly proportional to frequency; if you double f then E doubles. Frequency is inversely proportional to wavelength (since the speed of light is where λ (lambda) is the length of a wave.
How Planck constructed his model and performed his calculation is beyond the scope of this essay.
Photoelectric Effect 1905
[edit | edit source]
In 1905 Albert Einstein published a paper that explained experimental data from the photoelectric effect that occurs when light strikes a metal surface. The photoelectric effect is the emission of an electron from a substance when light is absorbed. electrons are emitted from solids, liquids or gases when they absorb energy from light. Electrons emitted in this manner may be called photoelectrons. His hypothesis was that the photon's energy frequecy obeyed (i.e. Eq. (1) ). Each photon was assumed to give all of its energy to a single electron, and the energy of this electron could be measured by measuring the voltage required to keep the electron from escaping from the metal.
More links on the Photoelectric effect
[edit | edit source]- http://phet.colorado.edu/en/simulation/photoelectric (Excellent simulation lab by University of Colorado Boulder's PhET effort.)
- https://en.wikiversity.org/wiki/Photoelectric_Effect_for_Beginners (A discussion similar to this one.}
Taylor makes things spooky with very dim light in 1909
[edit | edit source]

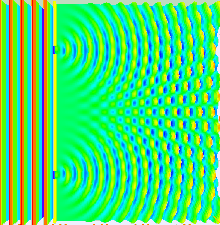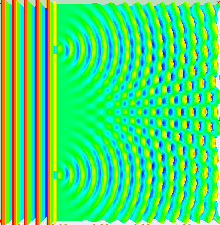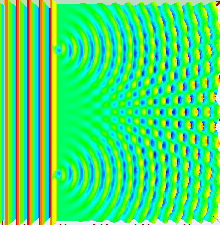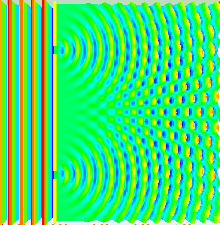
While studying medicine at Göttingen in the 1790s, Thomas Young wrote a thesis on the physical and mathematical properties of sound[14] and in 1799, he presented a paper to the Royal Society where he argued that light was also a wave. His idea was furiously opposed because it contradicted Newton, whose views were considered sacred. Nonetheless, he continued to develop his ideas. In 1801, he presented a famous paper to the Royal Society entitled "On the Theory of Light and Colours" [15] which described various interference phenomena, and in 1803 he performed his famous double-slit experiment (strictly speaking, a double hole experiment).
Diffraction occurs also with water and sound. Diffraction allows one to measure wavelength, and the same value of wavelength occurs for diffraction through single slits, double slits, and N-slits. The results are consistent with diffraction through a circular hole.
This experiment was repeated 100 years later by G. I. Taylor in light so dim that only one photon at a time was likely to be involved with the interference. Amazingly, one photon can interfere with itself. Shown in the figure to the right is a simulated animation of what is observed. Since the photons are passing one at a time, a time gap separates when each particle strikes the screen and creates a black dot. [16] The experiment has been repeated in recent years with electrons, atoms, and even molecules containing over 800 atoms.[17]
Bohr-Rutherford Model 1913
[edit | edit source]
The Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with attraction provided by electrostatic forces rather than gravity. The Bohr model is a primitive model of the hydrogen atom that has been surpassed by the more sophisticated Schrodinger's equation. Nevertheless, Bohr's calculation should be viewed as more than a lucky guess. A guess based on dimensional analysis using a new and controversial fundamental constant is also an educated guess. The Bohr model assumes circular orbits of radius, , and follows Newton's laws of physics, but with the following two embellishments to Newton's theory:
-
()
-
()
and is momentum. Lambda, or , is now known as the De Broglie wavelength (although Bohr did not use the De Broglie wavelength to construct this model.) For an electron of mass , and velocity , .[18]


The meaning of allowed orbits can be discerned from the pair of figures situated to the left. The wavelength must be such that the number that fit into a full circumference (2пr) must equal one, or two, or 3, or 4 (and so forth). In one case, the wave fits perfectly in the circles (with exactly four wavelengths). This corresponds to an electron in the third excited state, or n =4. The other wave does not fit into its allowed radius because it doubles over itself. This energy level does not exist for this atom.
Planck's relation (i.e. Eq.(1)) holds for the photons that are emitted from the hydrogen atom, with the photon energy, , being equal to the difference in energy between the two electron orbitals. This can be expressed as an energy conservation law:
- ,
where is the higher energy and is the lower energy of the atom. These energies were calculated using Newton's laws of physics, just as one would calculate the energy of a satellite orbiting the Earth. The frequency of the light, , could be measured by passing light the very hot gas (glowing) through a prism and measuring the wavelength.
While equations(1), (2), and (3) seem to embody all the calculations of Old Quantum Mechanics, they oversimplify the lines of reasoning actually used. Bohr, for example, did not use equation (3). And he wrote (2) not as a statement about "allowed" wavelengths, but about the quantization of angular momentum (L = mvr= nh/(2π)). In fact, the wave behavior of matter particles such as the electron (i.e., matter waves) was not suspected in 1913, and at that time Bohr did not believe in the existence of photons. [19]
Compton Effect 1923
[edit | edit source]

More evidence that Eq.(3) also holds for the momentum of an individual photon was provided by Arthur Holly Compton in 1923. Since the photon is generally understood to be massless, the momentum, , of the photon is not equal to , but equal to , where is the speed of light. The calculation of Compton scattering is a bit more difficult than those collisions usually studied in an undergraduate physics course because it is necessary to perform a relativistic calculation. Nevertheless, the calculation can be performed and predictions were confirmed by experimental observation.
de Broglie Waves 1924
[edit | edit source]| “ | When I conceived the first basic ideas of wave mechanics in 1923–24, I was guided by the aim to perform a real physical synthesis, valid for all particles, of the coexistence of the wave and of the corpuscular aspects that Einstein had introduced for photons in his theory of light quanta in 1905. | ” |
| — De Broglie[20] | ||

Today, the de Broglie relations[21] are more likely to be expressed using different variables. Instead of , it is more common to use (pronounced "h-bar"). Also, is defined as the wavenumber, is the angular frequency. In these variables, we have , and .
Although we are using the de Broglie relations within the context of the non-relativistic quantum theory, much of de Broglie's argument was based on Einstein's theory of special relativity, which describes how length, time, mass and energy are perceived by observers who are moving relative to one another. The figure on the left shows the crests and troughs of a travelling wave (in blue and red). Einstein's special theory of relativity inertial reference frames describes how different observers (moving at different speeds) will perceive length, time, speed, momentum, and energy. Self-consistency is possible only if frequency-wavenumber is proportional to energy-momentum. Mathematically, De Broglie derived only the need for this proportionality, not its value. But it was clear that ħ is that constant.
Schrödinger Wave Equation 1926
[edit | edit source]

Schrödinger put forth a wave equation that gave the correct energy levels of the hydrogen atom in 1926. [22] At last we have an equation from which a fundamental wave theory of quantum mechanics might be constructed.
-
()
Although Heisenberg, Born, and Jordan had already developed a parallel effort using matrices that would prove to be a mathematically equivalent theory[23]), we shall take this as the starting point in our quest for a fully developed theory. While this equation looks intimidating to a novice, it is a standard wave equation that is in many respects simpler than Maxwell's Equations. It is completely deterministic, meaning that it allows one to predict how a wave will evolve (given initial conditions). In other words, like Newton's , equation (4) predicts the future of the wave amplitude (We shall soon discover that predicting future values of ψ is not necessarily the same as predicting the future behavior of the particle.)

To the left are some computer generated solutions Schrödinger's equations for a (very tiny) mass attached to a spring. The symbol, ψ, is spelled psi, but often pronounced "sigh", with a hint of "p" at the beginning. It can also be pronounced "psee". It is called the "wavefunction", and is essentially the "amplitude", analogous to the "height" of the wave. The wavefunctions C through F represent states of known energy not unlike the "allowed" orbits of the Bohr atom. Wavefunctions G and H are more complicated and have no counterpart in Bohr's model of "allowed" states. They are known as "mixed energy" states.
What is the nature of the Wavefunction?
[edit | edit source]The Schrödinger equation details the behavior of ψ but says nothing of its nature. Schrödinger unsuccessfully tried to interpret it as a charge density. [24] More specifically it seemed plausible to interpret the square of the amplitude, |ψ|2, as a charge density, since the total charge can be shown to remain constant if ψ obeys Schrödinger's equation. Schrödinger always opposed a statistical or probabilistic approach, with its associated discontinuities—much like Einstein, who believed that quantum mechanics was a statistical approximation to an underlying deterministic theory— and never reconciled with the Copenhagen interpretation. In 1926, Max Born successfully interpreted ψ as the probability amplitude, whose absolute square,|ψ|2, is equal to probability density. [25] .[26] Like charge, probability also obeys a conservation law, namely that the sum of all probabilities always adds to 1 (i.e., 100%)
Even though Schrödinger is (correctly) credited with inventing this wave equation, a connection between waves and particle motion was understood as early as 1834 when Hamilton wrote equations that describe the path taken by light in the approximation that the wavelength is very small.
Davisson–Germer's accidental diffraction of electrons 1927
[edit | edit source]
While attempting to clean an oxide film off of nickel surface, Davisson and Germer heated the specimen to high temperature, not knowing that this would create large single crystal big enough to caused diffraction of their electron beam.[27][28]
Heisenberg's uncertainty principle 1927
[edit | edit source]Have you ever noticed that you can't ask a person what they are thinking without changing what they are thinking about? Here is what one of the founders of Quantum Mechanics had to say:
| “ | If a person tries to observe what he is thinking about at the very moment that he is reflecting on a particular subject, it is generally agreed that he introduces unpredictable and uncontrollable changes in the his thoughts proceed thereafter. Why this happens is not definitely known at the present, but some plausible explanations will be suggested later. | ” |
| — David Bohm[29] | ||
Heisenberg came up with more convincing understanding that learning about something changes it in an unpredictable way. His argument imagined a powerful but hypothetical microscope that could see the electron as it orbited around the nucleus. Combining his knowledge of optics with the Compton Effect, Heisenberg concluded that the light required to see the electron would drastically change its orbit. And if the light were gentle, with low-energy photons, the microscope would yield an image so blurred that it would be impossible to track the electron's path.
Measuring a particle at rest in a dark room
[edit | edit source]
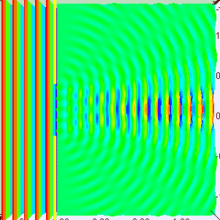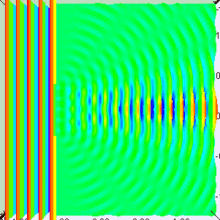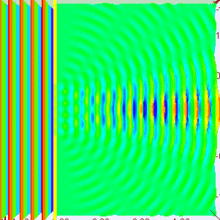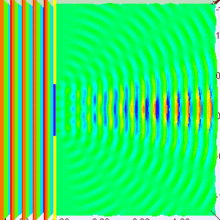
Suppose you are in large dark room with an electron that is known to be at rest. You want to measure its location. The room must be dark because light would interact with and induce motion in the electron. So you put a small hole in a large flat sheet and wave the sheet past where you think the electron is (there is of course no air in the room.) If the electron hits the sheet, your measurement was a failure. But if you repeat the experiment often enough, you will eventually succeed and have knowledge about where the electron is located. Since your sheet never touched the electron, is still at rest, right? Wrong!--No force ever acted on the electron; but nevertheless the electron has now been set in motion! Moreover, you don't know exactly how it is moving.
To understand why, put yourself reference frame of your flat sheet. The sheet is now at rest and an electron is moving towards it. By the de Broglie hypothesis, this electron will have wavelength (given by Eq. (3) to be h/mv). But if the electron acts as a wave, it will undergo single slit diffraction as shown in the figures to the left and right. Notice how decreasing the diameter of the hole increases the motion the spreading of the wave. The more you know about the position, the less you know about the motion, and vice versa. With a bit of basic algebra, the well-known equation for single slit diffraction can be shown to be consistent with the following inequality:
-
()
where , is the uncertainty in position, and is the uncertainty in momentum, . (The symbol is called "sigma"). Equation (5) is known as Heisenberg's uncertainty principle, and renowned theoretical physicists have spent hours attempting to violate it. Under the Copenhagen interpretation of quantum mechanics, it can be proven as a mathematical theorem.
Copenhagen interpretation
[edit | edit source]
The image to the left illustrates a simple argument for a probabilistic interpretation. Although the wave shown is not a solution to Schrodinger's equation. Wavepackets can become delocalized, hear by impinging on some sort of barrier. What attribute of a particle can be in two places at the same time? Probability! To create this situation in a classroom, tape a wooden block to a stretched snaky spring and strike it.

A detailed set of rules for interpreting ψ that is beyond our scope. But for reference, three fundamental features of these rules are stated:
- |ψ|2ΔV is the probability of the particle being inside a volume ΔV.
- If a wave function is a superposition of two or more states of known energy, the particle has a probability of being in any of those energy states. In particular, if ψ1 and ψ2 are normalized wavefunctions( ʃ|ψ|2dV=1), and if the (complex) amplitudes a1 and a2 are also normalized (i.e., |a1|2+|a2|2=1), then |a1|2 is the probability of having energy E1 and |a2|2 is the probability of having energy E2.
- If a measurement changes our understanding of the nature of any of the particle's attributes (energy, position, velocity, ...), then the wavefunction immediately rearranges itself in a process called the "collapsing of the wavefunction" .
Example 1: Minimum uncertainty within Copenhagen interpretation from repetitive measurement
[edit | edit source]We consider the perfect measurement when the dense grid of Maxwell's demons is used to detect the presence of the particle at certain coordinate at certain time who can catch the particle at the coordinates when they see it near. Let us consider the free particle with the mass in one spatial dimension in spreading Gaussian wave packet state:
where the spreading : evolves in time
According to the Copenhagen interpretation the position measurement will collapse the wave function to the eigenstate of the position operator (or back prepare it in this state)
To measure the momentum of the particle two consecutive measurements of the position must me done separated in time by to find the velocity first:
While the delta function may be well approximated by a Gaussian with the infinitesimal spread
- (the exact wave function is proportional to it)
the time evolution of the collapsed state between repetitive measurement which will be therefore
Therefore after each measurement the wave functions reconstructs itself by the free evolution of the spreading near-delta function and is only space shifted so the demolition measurements are nonetheless done effectively on the same quantum state. We can reset the center of the coordinate system to 0 after each measurement so if is the probability density distribution of each square of position measurement the average over many measurements is
The corresponding average of the momentum dispersion is immediately
or
Putting the between-measurement time infinitesimal before we get
or the minimum uncertainty.
Example 2: Minimum uncertainty of position and momentum in 3 dimensions
[edit | edit source]The uncertainty relation in more dimensions is exotic in the sense that coefficients appear at the front of . We want the uncertainty relation for
We will use the general relation for the uncertainty for the operators
We want the uncertainty relation for i.e. for the operators
The first step is to find the auxiliary operators such that this relation can be used directly. We must make therefore the same trick that Dirac made to calculate the square root of the Klein-Gordon operator to get the Dirac equation:
where are matrices from the Dirac equation:
Therefore we have
We can now readily calculate the commutator while using the anty-comutation properties of matrixes and noticing that the symmetric Gaussian state is annihilating in average the terms containing mixed variable like
Calculating 9 commutators (mixed may be zero by Gaussian example) we obtain
Therefore
which is 3 times (space dimension) more then for the one dimension.
Schrodinger's cat 1935
[edit | edit source]
The idea that an object can be in two places at the same time is unsettling, although there seems to be little evidence that this philosophical mystery has interfered with the pursuit of experimental or even theoretical physics. Three ideas have been put forth that have become cultural icons of Quantum Mechanics. They are the EPR Paradox, Schrodingers Cat, and Bell's Theorem (which has been justifiably called “the most profound discovery of science”.[30]) Of these three cultural icons, Schrodinger's cat is easiest to grasp. Schrödinger wrote:[31]
| “ | One can even set up quite ridiculous cases. A cat is penned up in a steel chamber, along with the following device (which must be secured against direct interference by the cat): in a Geiger counter, there is a tiny bit of radioactive substance, so small, that perhaps in the course of the hour one of the atoms decays, but also, with equal probability, perhaps none; if it happens, the counter tube discharges and through a relay releases a hammer that shatters a small flask of hydrocyanic acid. If one has left this entire system to itself for an hour, one would say that the cat still lives if meanwhile no atom has decayed. The psi-function of the entire system would express this by having in it the living and dead cat (pardon the expression) mixed or smeared out in equal parts.. | ” |
| — Erwin Schrödinger[32] | ||
Recent Developments
[edit | edit source]- 1964 – John Stewart Bell puts forth Bell's theorem
- 1982 - Bell's theorem was experimentally verified by Alain Aspect[33]
- 2010 - Cleland puts an object visible to the naked eye (but smaller than a cat) into a mixed energy state. [34]
Quiz
[edit | edit source]See the subpage for a quiz on this topic.
References and Endnotes
[edit | edit source]- Most of material was lifted out of Wikipedia
- ↑ https://en.wikipedia.org/wiki/Quantum_mechanics
- ↑ https://en.wikipedia.org/wiki/Old_quantum_theory
- ↑ https://en.wikipedia.org/w/index.php?title=Matrix_mechanics&oldid=577613976
- ↑ This analysis assumes that the speed is much less than that of light (i.e. w:nonrelativistic).
- ↑ There is a fourth condition for quantum mechanics to occur: when elementary particles collide at very high energy, they can interact with each in such a way as to create new particles. This is the field of High Energy Physics (or particle physics), and will not be part of our discussion, except in one minor way. In the Compton effect, the x-ray was "high energy" (in those days) and acts as a classical particle (like a billiard ball) that rips apart the atom.
- ↑ https://en.wikipedia.org/wiki/Timeline_of_quantum_mechanics
- ↑ Planck thought (perhaps correctly?) that it is not light but the way atoms behaved that was quantized.
- ↑ https://en.wikipedia.org/wiki/History_of_quantum_mechanics
- ↑ This and Plank's work begin to establish wave-particle duality for electromagnetic radiation (i.e., "light" is also a "particle"). Also, in the same year he publishes Special Theory of Relativity and proposes the equivalence of matter and energy. These ideas are later used by De Broglie to establish wave-particle duality for particles (i.e., the "particle" is also a "wave")
- ↑ Taylor, Geoffrey Ingram. "Interference fringes with feeble light." Proceedings of the Cambridge Philosophical Society. Vol. 15. No. 1. 1909.
- ↑ This is the first clue as to why atomic energy levels are quantized. In fact, except for the fact that it employs Planck's (fundamental) constant, h, the calculation was a lucky guess.
- ↑ https://en.wikipedia.org/w/index.php?title=Davisson%E2%80%93Germer_experiment&oldid=580087519
- ↑ Kuhn, T. S. (1978). Black-body theory and the quantum discontinuity 1894-1912. Oxford: Clarendon Press. ISBN 0195023838.
- ↑ Mason, P. (1981). The Light Fantastic. Penguin Books. ISBN 978-0-14-006129-1.
- ↑ Young, T. (1802). "The Bakerian Lecture: On the Theory of Light and Colours". Philosophical Transactions of the Royal Society of London 92: 12–48.
- ↑ Taylor, Geoffrey Ingram. "Interference fringes with feeble light." Proceedings of the Cambridge Philosophical Society. Vol. 15. No. 1. 1909.
- ↑ https://en.wikipedia.org/w/index.php?title=Double-slit_experiment&oldid=618587827
- ↑ Incidentally, this equation also holds for photons, where is the photon's momentum.
- ↑ https://en.wikipedia.org/wiki/Bohr_model
- ↑ Louis de Broglie "The Reinterpretation of Wave Mechanics" Foundations of Physics, Vol. 1 No. 1 (1970)
- ↑ L. de Broglie, Recherches sur la théorie des quanta (Researches on the quantum theory), Thesis (Paris), 1924; L. de Broglie, Ann. Phys. (Paris) 3, 22 (1925).
- ↑ https://en.wikipedia.org/wiki/Schrodinger
- ↑ https://en.wikipedia.org/wiki/Quantum_mechanics
- ↑ Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. p. 219. ISBN 0-521-43767-9.
- ↑ Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. p. 220. ISBN 0-521-43767-9.
- ↑ It is clear that even in his last year of life, as shown in a letter to Max Born, that Schrödinger never accepted the Copenhagen interpretation (cf. p. 220). Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. p. 479. ISBN 0-521-43767-9.
- ↑ Hugh D. Young, Roger A. Freedman: University Physics, Ed. 11. Pearson Education, Addison Wesley, San Francisco 2004, 0-321-20469-7, S. 1493-1494.
- ↑ https://en.wikipedia.org/w/index.php?title=Davisson%E2%80%93Germer_experiment&oldid=580087519
- ↑ Bohm, David. Quantum Theory, Dourier Dover Publications, 1951]
- ↑ Henry P. Stapp, "Bell's Theorem and World Process", Nuovo Cimento, Vol. 29B, No. 2, p. 270 (1975). (Quote on p. 271)
- ↑ Schroedinger: "The Present Situation in Quantum Mechanics." 5. Are the Variables Really Blurred?
- ↑ Die gegenwärtige Situation in der Quantenmechanik (The present situation in quantum mechanics), Naturwissenschaften
(translated by John D. Trimmer in Proceedings of the American Philosophical Society)] - ↑ in what might be the most philosophically profound experiment ever performed
- ↑ http://www.nature.com/news/2010/100317/full/news.2010.130.html Andrew Cleland at the University of California, Santa Barbara, and his team cooled a tiny metal paddle until it reached its quantum mechanical 'ground state' — the lowest-energy state permitted by quantum mechanics. They then used the weird rules of quantum mechanics to simultaneously set the paddle moving while leaving it standing still.


























![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[{\frac {-\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} ,t)\right]\Psi (\mathbf {r} ,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4894f9a205c471cb012351a1fccdd01285b6f11c)





![{\displaystyle |\psi (x,t)|^{2}=[2\pi \Delta x(t)^{2}]^{-1/2}e^{-{\frac {x^{2}}{2\Delta x(t)^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fde7e8fec54ec325a9cd29a52411e7c5286c5466)
















![{\displaystyle \sigma _{A}\sigma _{B}\geq {\frac {1}{2}}\left|\langle [{\hat {A}},{\hat {B}}]\rangle \right|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5839d5300a8ccfa7f2345e67a203729ebfe0e3)












![{\displaystyle \left|\langle [{\tilde {r}},{\tilde {p}}]\rangle \right|=3\hbar .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61271d361ded0120a42a338fa3079ca694a9f9e5)

