Quantum mechanics/Origin of quantum mechanics

Subject classification: this is a physics resource.

Type classification: this is a lesson resource.

Classical physics is essentially all physics known at the beginning of the 20th century. It included classical mechanics (Newton's laws), classical thermodynamics (see Thermodynamics), and electromagnetism (Maxwell's equations). At the beginning of the 20th century, a number of experiments could not be explained using the known physics. Some of these were:

• photoelectric effect
• spectrum of atoms
• radiation of the black body
• heat capacity of solids
• stability of the hydrogen atom.

All of these experiments have to do with the microscopic structure of matter and the behaviour of the elementary particles (electrons and protons) that were discovered at the same time. Several attempts by groups of scientists were made to understand these experiments. The theory now called quantum mechanics is the result.

Photoelectric effect

The red arrows represent incoming light which is absorbed by the rectangular metal place. Electrons (blue arrows) are emitted.

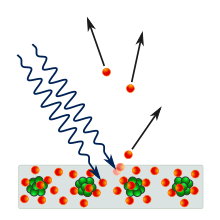
Metal surfaces irradiated with electromagnetic radiation with frequency v emit electrons only if the frequency of the incident radiation is larger than a threshold frequency. The threshold corresponds to the energy required to extract an electron from the metal (this is called the work function) but the dependence on the frequency of the light was unexpected. The energy of a classical wave is proportional to the square of the amplitude not of the frequency. Einstein postulated that the energy of light comes in packets of energy proportional to the frequency hv which can be thought of as "packets of light" or photons. h=6.62x10^-34 J s is Planck's constant.

Electromagnetic radiation is made by 'particles' called photons with energy hv.

Spectra of atoms

Atoms in the gas phase absorb radiation at very well defined wavelengths. The absorption spectrum of hydrogen was characterized a great deal. Without understanding the reason, it seemed that the absorption wavelengths obeyed the formula:
${\frac {1}{\lambda }}=R_{H}\left({\frac {1}{n^{2}}}-{\frac {1}{m^{2}}}\right)$
where n and m are any integer, and R_H is a constant.

Atoms appear to have discrete energy levels.

Heat capacity of solids and the radiation of the black body

Scientists did not know how solids were made but they did correctly assume that they were made by charged particles oscillating around some equilibrium position. The classical view was that heating up the system would increase the amplitude of the oscillations. Classical theory predicts that the heat capacity of the solid should not change with temperature. Contrary to the theory, the heat capacity of a solid goes to zero as temperature goes to zero.

Another phenomenon which was not understood with classical physics was the emission spectrum of the black body (this is too complicated to discuss here). Planck noted that both these phenomena could be explained if we assume that the oscillators in the solid with frequency v can only absorb and emit discrete quantities of energy hv. In classical physics an oscillator could exchange any amount of energy with the environment.

Oscillators of frequency v can only absorb/emit a quantity hv of energy.

Stability of the hydrogen atom

After the discovery that the hydrogen atom is made of one electron and one proton, any physicist knew that you couldn't describe the electron as "orbiting" around the proton. According to Maxwell's classical equation of electromagnetism, such an orbiting electron would emit radiation, lose kinetic energy and collapse on the nucleus of the atom.

The electron cannot orbit around the nucleus according to classical physics.

The Bohr atom

Bohr proposed an ad hoc model of the hydrogen atom. He said that the electron does orbit around the nucleus in a plane with fixed values of the angular momentum (though this left unexplained why it doesn't emit radiation). He said that the angular momentum (L = μvR where μ is the electron mass, v is the velocity, and R is the distance from the nucleus) is quantized and can only be a multiple of the constant ħ, where ħ = h ÷ 2π. The energy levels predicted by this model are correct but other aspects are not.

A model of the hydrogen atom that explains the experiments can be built if the electron angular momentum is quantized (i.e. it can only take discrete values).

The idea of de Broglie

Trying to find some more general explanation of the Bohr atom, de Broglie proposed that the electrons and all microscopic particles can be described as waves. The atom is a system that emits characteristic frequency is analogous to a musical instrument that can only give out fixed notes. Some of the experiments could be explained if a particle with momentum p = mv is associated to a wave with wavelength h ÷ p.

Note you can derive this equation from combining Einstein's equation $E=mc^{2}$, Planck's equation $E=hf$, and the classic wave formula that $f\lambda =c$.

Combining the first two and eliminating $E$ yields:

$hf=mc^{2}$

Then substituting $f={\frac {c}{\lambda }}$ gives:

${\frac {hc}{\lambda }}=mc^{2}$, and so

${\frac {h}{\lambda }}=mc=p$

A particle also behaves as a wave with wavelength λ = h / p.

Heisenberg and Schrodinger

The various ideas were a bit unconnected and it took about 20 years to develop a coherent theory now known as quantum mechanics. This version will explained as follows:

• Principles of quantum mechanics (approximate solutions) - Lesson 2
• A few applications and examples (exactly solvable cases) - Lessons 3-7
• Postulates of quantum mechanics (rigorous versions of the theory) - Lessons 8-9
• Spin and multielectron systems - Lessons 10-13

Exercise Define the following: mass, force, velocity, kinetic energy, potential energy, linear momentum. You need to know what all these quantities are. Define the following: wavelength, frequency, propagation velocity, interference, diffraction. You need to remember what these concepts about waves are. Summarize the experiments that prove something is wrong with classical physics. Calculate the de Broglie wavelength of: an electron with velocity 100 m/s a bullet weighing 20g with the same speed. The kinetic energy of a monatomic gas is ½kBT (kB is the Boltzmann constant). Calculate the de Broglie wavelength of an argon atom at a temperature of 300 K with this energy. In many classical physics applications (lenses, mirrors etc) light is assumed to propagate as a straight line (like a particle, not a wave). However, when light interacts with objects of dimension similar to its wavelength, the typical phenomena of waves (diffraction, interference) appear. Using your answers to question 4, explain why, according to de Broglie, an electron in a solid should behave more like a wave and a bullet in a shooting range should behave more like a particle. To estimate how small an object should be to behave like a wave, consider a cube of length L, velocity 10 m/s, and density ρ = 1000 Kg/m³ (typical of a solid). If L is large, this will behave as a classical object; if L is small, like a quantum object. Estimate the length of L below which quantum effects are important.

Next: Lesson 2 - The Essential Ideas