Jump to content

Properties of quarks

Add links
From Wikiversity

Electric charge

[edit | edit source]
See also: Electric charge

Quarks have fractional electric charge values—either −​1⁄3 or +​2⁄3 times the elementary charge, depending on flavor. Up, charm, and top quarks (collectively referred to as up-type quarks) have a charge of +​2⁄3, while down, strange, and bottom quarks (down-type quarks) have −​1⁄3. Antiquarks have the opposite charge to their corresponding quarks; up-type antiquarks have charges of −​2⁄3 and down-type antiquarks have charges of +​1⁄3. Since the electric charge of a hadron is the sum of the charges of the constituent quarks, all hadrons have integer charges: the combination of three quarks (baryons), three antiquarks (antibaryons), or a quark and an antiquark (mesons) always results in integer charges.[1] For example the hadron constituents of atomic nuclei, neutrons and protons, have charges of 0 and +1 respectively; the neutron is composed of two down quarks and one up quark, and the proton of two up quarks and one down quark.[2]

Spin

[edit | edit source]
See also: Spin (physics)

Spin is an intrinsic property of elementary particles, and its direction is an important degree of freedom. It is sometimes visualized as the rotation of an object around its own axis (hence the name "spin"), though this notion is somewhat misguided at subatomic scales because elementary particles are believed to be point-like.[3]

Spin can be represented by a vector whose length is measured in units of the reduced Planck constant ħ (pronounced "h bar"). For quarks, a measurement of the spin vector component along any axis can only yield the values +ħ/2 or −ħ/2; for this reason quarks are classified as spin-​1⁄2 particles.[4] The component of spin along a given axis—by convention the z axis—is often denoted by an up arrow ↑ for the value +​1⁄2 and down arrow ↓ for the value −​1⁄2, placed after the symbol for flavor. For example, an up quark with a spin of +​1⁄2 along the z axis is denoted by u↑.[5]

Weak interaction

[edit | edit source]
Main resource: Weak interaction
A tree diagram consisting mostly of straight arrows. A down quark forks into a up quark and a wavy-arrow W[superscript minus] boson, the latter forking into an electron and reversed-arrow electron antineutrino.
Feynman diagram of beta decay with time flowing upwards. The CKM matrix (discussed below) encodes the probability of this and other quark decays.

A quark of one flavor can transform into a quark of another flavor only through the weak interaction, one of the four fundamental interactions in particle physics. By absorbing or emitting a W boson, any up-type quark (up, charm, and top quarks) can change into any down-type quark (down, strange, and bottom quarks) and vice versa. This flavor transformation mechanism causes the radioactive process of beta decay, in which a neutron (n) "splits" into a proton (p), an electron (e−
) and an electron antineutrino (ν
e) (see picture). This occurs when one of the down quarks in the neutron (udd) decays into an up quark by emitting a virtual W−
 boson, transforming the neutron into a proton (uud). The W−
 boson then decays into an electron and an electron antineutrino.[6]

  n →   p + e−
 + ν
e		 (Beta decay, hadron notation)
udd → uud + e−
 + ν
e		 (Beta decay, quark notation)

Both beta decay and the inverse process of inverse beta decay are routinely used in medical applications such as positron emission tomography (PET) and in high-energy experiments such as neutrino detection.

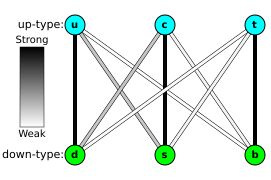
Three balls "u", "c", and "t" noted "up-type quarks" stand above three balls "d", "s", "b" noted "down-type quark". The "u", "c", and "t" balls are vertically aligned with the "d", "s", and b" balls respectively. Colored lines connect the "up-type" and "down-type" quarks, with the darkness of the color indicating the strength of the weak interaction between the two; The lines "d" to "u", "c" to "s", and "t" to "b" are dark; The lines "c" to "d" and "s" to "u" are grayish; and the lines "b" to "u", "b" to "c", "t" to "d", and "t" to "s" are almost white.
The strengths of the weak interactions between the six quarks. The "intensities" of the lines are determined by the elements of the CKM matrix.

While the process of flavor transformation is the same for all quarks, each quark has a preference to transform into the quark of its own generation. The relative tendencies of all flavor transformations are described by a mathematical table, called the Cabibbo–Kobayashi–Maskawa matrix (CKM matrix). The approximate magnitudes of the entries of the CKM matrix are:[7]

where Vij represents the tendency of a quark of flavor i to change into a quark of flavor j (or vice versa).[8]

There exists an equivalent weak interaction matrix for leptons (right side of the W boson on the above beta decay diagram), called the Pontecorvo–Maki–Nakagawa–Sakata matrix (PMNS matrix).[9] Together, the CKM and PMNS matrices describe all flavor transformations, but the links between the two are not yet clear.[10]

Strong interaction and color charge

[edit | edit source]
See also: Color charge and Strong interaction
A green and a magenta ("antigreen") arrow canceling out each other out white, representing a meson; a red, a green, and a blue arrow canceling out to white, representing a baryon; a yellow ("antiblue"), a magenta, and a cyan ("antired") arrow canceling out to white, representing an antibaryon.
All types of hadrons have zero total color charge.

Quarks possess a property called color charge. There are three types of color charge, arbitrarily labeled blue, green, and red.[11] Each of them is complemented by an anticolor—antiblue, antigreen, and antired. Every quark carries a color, while every antiquark carries an anticolor.</ref> R. Nave. "The Color Force". HyperPhysics. Georgia State University, Department of Physics and Astronomy. Retrieved 2009-04-26.</ref>

The system of attraction and repulsion between quarks charged with different combinations of the three colors is called strong interaction, which is mediated by force carrying particles known as gluons; this is discussed at length below. The theory that describes strong interactions is called quantum chromodynamics (QCD). A quark charged with one color value can form a bound system with an antiquark carrying the corresponding anticolor; three (anti)quarks, one of each (anti)color, will similarly be bound together. The result of two attracting quarks will be color neutrality: a quark with color charge ξ plus an antiquark with color charge −ξ will result in a color charge of 0 (or "white" color) and the formation of a meson. Analogous to the additive color model in basic optics, the combination of three quarks or three antiquarks, each with different color charges, will result in the same "white" color charge and the formation of a baryon or antibaryon.[12]

In modern particle physics, gauge symmetries—a kind of symmetry group—relate interactions between particles (see gauge theories). Color SU(3) (commonly abbreviated to SU(3)c) is the gauge symmetry that relates the color charge in quarks and is the defining symmetry for quantum chromodynamics.[13] Just as the laws of physics are independent of which directions in space are designated x, y, and z, and remain unchanged if the coordinate axes are rotated to a new orientation, the physics of quantum chromodynamics is independent of which directions in three-dimensional color space are identified as blue, red, and green. SU(3)c color transformations correspond to "rotations" in color space (which, mathematically speaking, is a complex space). Every quark flavor f, each with subtypes fB, fG, fR corresponding to the quark colors,[14] forms a triplet: a three-component quantum field which transforms under the fundamental representation of SU(3)c.[15] The requirement that SU(3)c should be local—that is, that its transformations be allowed to vary with space and time—determines the properties of the strong interaction, in particular the existence of eight gluon types to act as its force carriers.[13][16]

Mass

[edit | edit source]
See also: Mass

Two terms are used in referring to a quark's mass: current quark mass refers to the mass of a quark by itself, while constituent quark mass refers to the current quark mass plus the mass of the gluon particle field surrounding the quark.[17] These masses typically have very different values. Most of a hadron's mass comes from the gluons that bind the constituent quarks together, rather than from the quarks themselves. While gluons are inherently massless, they possess energy—more specifically, quantum chromodynamics binding energy (QCBE)—and it is this that contributes so greatly to the overall mass of the hadron (see mass in special relativity). For example, a proton has a mass of approximately 938 MeV/c2, of which the rest mass of its three valence quarks only contributes about 11 MeV/c2; much of the remainder can be attributed to the gluons' QCBE.[18][19]

The Standard Model posits that elementary particles derive their masses from the Higgs mechanism, which is related to the unobserved Higgs boson. Physicists hope that further research into the reasons for the top quark's large mass, which was found to be approximately equal to that of a gold nucleus (~171 GeV/c2),[18][20] might reveal more about the origin of the mass of quarks and other elementary particles.[21]

Table of properties

[edit | edit source]
See also: Flavor (particle physics)

The following table summarizes the key properties of the six quarks. Flavor quantum numbers (isospin (I3), charm (C), strangeness (S, not to be confused with spin), topness (T), and bottomness (B′)) are assigned to certain quark flavors, and denote qualities of quark-based systems and hadrons. The baryon number (B) is +​1⁄3 for all quarks, as baryons are made of three quarks. For antiquarks, the electric charge (Q) and all flavor quantum numbers (B, I3, C, S, T, and B′) are of opposite sign. Mass and total angular momentum (J; equal to spin for point particles) do not change sign for the antiquarks.

Quark flavor properties[18]
Name Symbol Mass (MeV/c2)* J B Q I3 C S T B′ Antiparticle Antiparticle symbol
First generation
Up u 1.7 to 3.3 ​1⁄2 +​1⁄3 +​2⁄3 +​1⁄2 0 0 0 0 Antiup u
Down d 4.1 to 5.8 ​1⁄2 +​1⁄3 −​1⁄3 −​1⁄2 0 0 0 0 Antidown d
Second generation
Charm c 1270++70
−90 		​1⁄2 +​1⁄3 +​2⁄3 0 +1 0 0 0 Anticharm c
Strange s 101++29
−21 		​1⁄2 +​1⁄3 −​1⁄3 0 0 −1 0 0 Antistrange s
Third generation
Top t 172000±900  ±1,300  ​1⁄2 +​1⁄3 +​2⁄3 0 0 0 +1 0 Antitop t
Bottom b 4190++180
−60 		​1⁄2 +​1⁄3 −​1⁄3 0 0 0 0 −1 Antibottom b
J = total angular momentum, B = baryon number, Q = electric charge, I3 = isospin, C = charm, S = strangeness, T = topness, B′ = bottomness.
* Notation such as 4190++180
−60 denotes measurement uncertainty. In the case of the top quark, the first uncertainty is statistical in nature, and the second is systematic.

References

[edit | edit source]
  1. ↑ G. Fraser (2006). The New Physics for the Twenty-First Century. Cambridge University Press. p. 91. ISBN 0521816009. 
  2. ↑ M. Munowitz (2005). Knowing. Oxford University Press. p. 35. ISBN 978-0-19-516737-5.
  3. ↑ "The Standard Model of Particle Physics". BBC. 2002. Retrieved 2009-04-19.
  4. ↑ F. Close (2006). The New Cosmic Onion. CRC Press. pp. 80–90. ISBN 1584887982. 
  5. ↑ D. Lincoln (2004). Understanding the Universe. World Scientific. p. 116. ISBN 9812387056. 
  6. ↑ "Weak Interactions". Virtual Visitor Center. Stanford Linear Accelerator Center. 2008. Retrieved 2008-09-28.
  7. ↑ K. Nakamura et al. (2010). "Review of Particles Physics: The CKM Quark-Mixing Matrix". J. Phys. G 37 (075021): 150. http://pdg.lbl.gov/2010/reviews/rpp2010-rev-ckm-matrix.pdf. 
  8. ↑ The actual probability of decay of one quark to another is a complicated function of (amongst other variables) the decaying quark's mass, the masses of the decay products, and the corresponding element of the CKM matrix. This probability is directly proportional (but not equal) to the magnitude squared (|Vij|2) of the corresponding CKM entry.
  9. ↑ Z. Maki, M. Nakagawa, S. Sakata (1962). "Remarks on the Unified Model of Elementary Particles". Progress of Theoretical Physics 28 (5): 870. doi:10.1143/PTP.28.870. http://ptp.ipap.jp/link?PTP/28/870/pdf. 
  10. ↑ B.C. Chauhan, M. Picariello, J. Pulido, E. Torrente-Lujan (2007). "Quark–lepton complementarity, neutrino and standard model data predict θPMNS
    13     = 9++1
    −2     °    ". European Physical Journal C50 (3): 573–578. doi:10.1140/epjc/s10052-007-0212-z. arXiv:hep-ph/0605032.     
  11. ↑ Despite its name, color charge is not related to the color spectrum of visible light.
  12. ↑ B.A. Schumm (2004). Deep Down Things. Johns Hopkins University Press. pp. 131–132. ISBN 080187971X. OCLC 55229065. 
  13. ↑ 13.0 13.1 Part III of M.E. Peskin, D.V. Schroeder (1995). An Introduction to Quantum Field Theory. Addison–Wesley. ISBN 0-201-50397-2. 
  14. ↑ V. Icke (1995). The force of symmetry. Cambridge University Press. p. 216. ISBN 052145591X. 
  15. ↑ M.Y. Han (2004). A story of light. World Scientific. p. 78. ISBN 9812560343. 
  16. ↑ C. Sutton. "Quantum chromodynamics (physics)". Encyclopædia Britannica Online. Retrieved 2009-05-12.
  17. ↑ A. Watson (2004). The Quantum Quark. Cambridge University Press. pp. 285–286. ISBN 0521829070. 
  18. ↑ 18.0 18.1 18.2 K. Nakamura et al. (Particle Data Group) (2010). "Review of Particle Physics: Quarks". Journal of Physics G 37: 075021. doi:10.1088/0954-3899/37/7A/075021. http://pdg.lbl.gov/2010/tables/rpp2010-sum-quarks.pdf. 
  19. ↑ W. Weise, A.M. Green (1984). Quarks and Nuclei. World Scientific. pp. 65–66. ISBN 9971966611. 
  20. ↑ D. McMahon (2008). Quantum Field Theory Demystified. McGraw–Hill. p. 17. ISBN 0071543821. 
  21. ↑ S.G. Roth (2007). Precision electroweak physics at electron–positron colliders. Springer. p. VI. ISBN 3540351647. 
Retrieved from "https://en.wikiversity.org/w/index.php?title=Properties_of_quarks&oldid=2160009"