Polar Coordinates

From the Unit Circle to Polar Coordinates: A Step-by-Step Exploration of the Origins of Polar Coordinates

This is specifically geared for high school students to thoroughly and deeply understand the concept of polar coordinates by relating their knowledge of geometric construction and the unit circle to polar coordinates, and then extended into the complex plane and a discussion of Euler's Identity.

The Unit Circle

There are tons of websites that talk about the unit circle, but few take the time to derive it and really dig into it. Here are a few that are examples of the majority of information available online about the unit circle:

http://www.mathsisfun.com/geometry/unit-circle.html

To find where Polar Coordinates come from and why they matter, it is important to start with a thorough understanding of the unit circle and how this leads to definitions of sine and cosine. To do this, it is necessary to construct the unit circle, which can be defined as a circle with radius 1 centered at the origin, (0,0).

Construct this circle and label each point where the circle intersects the axes, giving (1,0), (0,1), (-1,0), (0,-1). Define a start point for the radius. From the common notion of a unit circle, let this start point be defined by the radius forming a 0° angle with the positive x axis, which gives the first of these four points, (1,0). At this point, there has been no rotation of the radius around the circle yet. Then consider (0,1), which lies on the y-axis. By definition of the Cartesian axes, the angle formed by the 1 unit long radius at this point and the positive x-axis is a 90° angle, the same angle separating the y-axis and x-axis. Adding 90° to this angle between the unit radius and the positive x-axis at the point (0,1), the radius would then have rotated 180° from its starting position on the positive x-axis and will intersect the edge of the circle at (-1,0), so this point is reached by a 180° rotation. Repeating this addition of 90° from the 180° rotated radius touching (-1,0) would be a total rotation of 270° and would rotate the unit radius down to touch the point (0,-1). Completing a 360° rotation around the unit circle by adding 90° one more time puts the radius back at the point (1,0), the start point. Values found so far: (1,0) = 0° and 360°, (0,1) = 90°, (-1,0) = 180°, (0,-1) = 270°. (figure 1)

Then construct the perpendicular bisector of the x axis between the origin and the point (1,0) and a line segment that goes from the midpoint on the x axis through the intersection point of the perpendicular bisector and the unit circle. Connect the point of intersection on the circle with the origin with a straight line segment. This now makes a right triangle with a base of ½ because it is the perpendicular bisector of a line segment that is 1 unit in length. Because the hypotenuse of the triangle goes from the origin to the edge of the circle, it is a radius of the unit circle and thus 1 unit in length. This gives two values for use in the Pythagorean Theorem with

a^{2}+b^{2}=c^{2}

\left({\frac {1}{2}}\right)^{2}+b^{2}=(1)^{2}

{\frac {1}{4}}+b^{2}=1

b^{2}={\frac {3}{4}}

b=\pm {\frac {\sqrt {3}}{2}}

Choosing the positive value for b since the point is in the first quadrant, the value for the point on the edge of the circle is $(1/2,{\sqrt {3}}/2)$ . Reflecting over the x axis and over the y axis, this gives four points along the unit circle to mark (figure 2)

Repeating the procedure used to find the $(1/2,{\sqrt {3}}/2)$ family, but with perpendicular bisectors constructed through the y-axis, there is a y value of ½ and a radius of 1, and using this in the Pythagorean Theorem, the corresponding x value at this point is ${\sqrt {3}}/2$ . By the same procedure, reflecting it over the x and y axis, there are 4 new points on the circle.

Now consider the newly drawn (orange in figure 3) line segment in quadrant one that goes from the origin to a point on the edge of the unit circle and its reflection in quadrant four (green in figure 3). These are the same length because they are just a reflection of the same line. Constructing a line between the two points where these lines intersect the circle, there is a third line (pink), completing a triangle. The orange and green lines were made using the perpendicular bisector of the y axis and so they form the diagonal of a rectangle with the x and y axis (the segment on the y in teal), the perpendicular bisector and half of the pink line. So the pink line is twice the measure of the teal line, which is ½ unit from earlier, so twice this is 1 unit, which is the total length of the pink line. This means that all 3 legs of the pink/green/orange triangle are all 1 unit in length (the other two because they are radii) and so each of the angles in the triangle is 60°. This is bisected by the x axis because the angle is the result of a reflection over the x-axis, so each angle defining the point family $({\sqrt {3}}/2,1/2)$ is 30°, and to repeat this logic with the lines that define the $(1/2,{\sqrt {3}}/2)$ , the angle made with the x axis for each of those is 60°. Then progressing through the point family, each angle is an iteration of 60° that defines its point.

Then consider the 90° angle made by the x and y axes. Draw the angle bisector from the origin to the point on the unit circle which can be done by constructing a line segment from (0,1) to (1,0). Then construct the perpendicular bisector of this line. This should go through the origin and through the unit circle. Since this bisects the 90° angle formed by the axes, this point is defined by a 45° angle, and since there are 180° in a triangle, 180-90 (from the dotted gray line from the x axis to the point on the circle where the gray line (angle bisector) and circle meet in figure 4)-45 = 45. Since the 2 angles are the same, the corresponding legs of the triangle have to be the same so using the Pythagorean Theorem:

a^{2}+a^{2}=1^{2}

2a^{2}=1

a^{2}={\frac {1}{2}}

a=\pm {\frac {\sqrt {2}}{2}}

So the point where the gray line touches the unit circle is $({\sqrt {2}}/2,{\sqrt {2}}/2)$ . Reflecting this gray line around the circle gives all the $({\sqrt {2}}/2,{\sqrt {2}}/2)$ family points. Figure 4 is what the final basic unit circle should look like.

Where Trigonometric Functions come from on the Unit Circle

Then open an Excel spreadsheet and label 3 columns “angle” “x” and “y” and fill in the angle values for every point on the unit circle as constructed in the “angle” column. Then fill in all the x values of each of the points marked by the angles (their points on the unit circle) and then do the same for the y values of these points, matching them up with the angles that have been inputted already. Then make two scatter plots, one that compares the angle column to x and one that compares the angle column to the y column. These will give the graphs of cosine and sine respectively. This shows that sine and cosine are just representative of ratios that hold between side lengths and angles in any triangle, and these graphs show how that ratio changes as it is rotated around the unit circle.

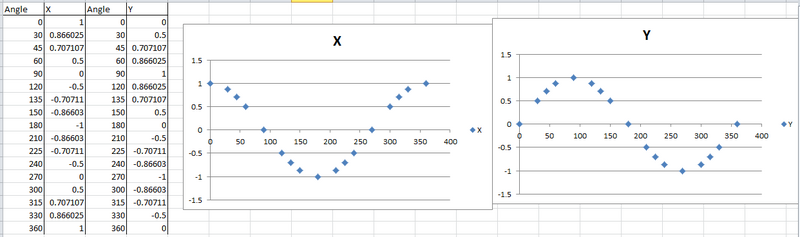
Every value found on the unit circle was found using Pythagorean Theorem, with the x value and y value being used for the two legs and the hypotenuse being universally equal to 1. The Excel graphs show that the sine curve is formed by all the y values and the cosine curve is formed by the x values so in the unit circle,

x^{2}+y^{2}=1^{2}

so

\cos ^{2}(\theta )+\sin ^{2}(\theta )=1^{2}

So sinθ is simply the y value of the point at the end of a radius of a circle where it touches the circle at an angle of θ with the positive x-axis and cosθ is simply the x value of the same point.

It should be noted that the unit circle gives cosθ = cos(180-θ) where 180-θ is the value of the angle between the radius and the negative x-axis when in the positive half with respect to the y-coordinate. Similarly, sinθ = sin(180-θ) as well (figure 6). This means it doesn’t matter which direction θ is measured from, as long as the half plane is either the upper or lower half plane. This will be important shortly.

The Tangent Function

The third major trigonometric function that plays a role in polar coordinates is the tangent function. To find and understand this function, it must also be constructed. A tangent line is one that has the slope of the function at a given point and touches the function only at that point. Circles have a unique property that the tangent line at any point on the circle forms a 90° angle with a radius of that circle. So constructing that line on a unit circle would look like figure 8.

There are two right triangles formed, one the standard right triangle that is formed with the radius of the unit circle (∆ABC), the other formed by the radius, the tangent line and the x-axis (∆ACD). Since θ is shared in both ∆ACD and ∆ABC and both triangles contain a right angle $\angle ABC\cong \angle ACD$ , by angle-angle, ∆ABC≈∆ACD. Because they are similar, their corresponding sides are proportional. The two triangles can be pulled apart to show these correspondences. Then it is clear that ${\tfrac {AC}{AB}}={\tfrac {DC}{CB}}$ and using the names of the sides find that ${\tfrac {1}{\cos(\theta )}}={\tfrac {\text{Tangent}}{\sin(\theta )}}$ . Solving algebraically, ${\tfrac {\sin(\theta )}{\cos(\theta )}}={\text{Tangent}}$

By inspection it is visible that tangent is dependent on θ (at $\angle A$ ), since as C and D get closer together, θ will get smaller. Additionally, the line tangent will move as cosθ and sinθ change, which both depend on θ, so renaming: $\tan(\theta )={\tfrac {\sin(\theta )}{\cos(\theta )}}$ or $\tan(\theta )={\tfrac {y}{x}}$

Radians

This is here to provide a holistic approach to the topic. A few other resources that discuss radians, including some interesting history are:

http://en.wikipedia.org/wiki/Radian

http://www.mathsisfun.com/geometry/radians.html

A radian is a way to express parts of a circle or divide up a circle into parts by measuring the length around the unit circle between two lines by extending two line segments from the center to the edge of the circle to form an angle at the center. In other words, radians express the arc length formed by some angle θ at the origin of the unit circle. To extend this to a circle with any radius, simply scale this by the radius, so the arc length at θ at the center of a circle is r*π. While this arc length can be expressed using degrees, degrees are man-made to make radians seem a little bit nicer. But let’s think about π. Where does π come from? π is the naturally occurring ratio of a circumference/diameter. It is universally true that the circumference divided by its diameter is π and this can be proved by investigating any circle on earth by measuring its diameter and measuring its circumference and then dividing circumference by diameter. It will always equal π! So π is naturally occurring, widely applicable and incredibly important as this ratio holds all throughout nature, science and mathematics. Then express θ in terms of π for any angle in the unit circle. Using the definition of π, c/d= π , π must be the arc that is one half of the circumference since the diameter cuts the circle in half. So if π is the arc length of half of the circle then it makes sense that twice this, 2π, must be the arc length of the whole circle, or the circumference, so if this arc were defined by tracing a point on the circle at with radius 1, moving the point from its starting point all the way back to that starting point moves the point 2π radians.

So conversion to between degrees and radians is defined using an understanding of radians: if π represents half of a circle, the angle in degrees would be 180 degrees in a degree based circle (half of 360°). So then if π=180°, ${\tfrac {\pi }{180^{\circ }}}=1={\tfrac {180^{\circ }}{\pi }}$ . This provides a handy conversion factor that does not change the value of the angle. To convert from degrees, use the conversion factor with degrees in the denominator (π/(180°)) so it cancels out the degree unit in the angle leaving only radians. Similarly, when converting from radians to degrees, use the conversion factor with the radian measure in the denominator ((180°)/π) which will only leave a degree value in the angle.

Polar coordinates and Defining the Polar Coordinate Axes

Any right triangle can be defined on a circle with radius r. The hypotenuse would be length r, and each leg of the right triangle formed by dropping a perpendicular from the point to the x-axis would also have to be scaled by r, meaning any point along the circle with radius r would have the coordinates (rcosθ, rsinθ) (figure 9).

Place concentric circles on the graph centered at the origin with varying radii and rays extending from the origin with different angles between the radii and the x-axis. This allows the conceptualization of the polar plane. (figure 10)

The center point is called the pole or origin, and extending from the origin to the right is the polar axis, which is in the same position as the positive x-axis in the Cartesian plane. Points on the polar coordinate system are represented as (r,θ), where θ is the angle that the point forms with the polar axis and the line connecting the point and the origin. The distance along that line to the point is represented by r, and can be considered as a radius of one of the concentric circles. If the distance is measured counter clockwise from the polar axis, the angle θ is positive, but if the angle is measured clockwise from the polar axis, θ is negative. If r is positive, it is measured on the line determined by θ. If r is negative, it is measured across the origin from its line specified by θ. So $(r,\theta )=(-r,360^{\circ }-\theta )$ and $(-r,\theta )=(-r,-(180^{\circ }-\theta ))=(r,360^{\circ }-\theta )$ (figure 11).

Each point in the polar plane can be translated back to the Cartesian plane using the right triangle method, giving that each point in the polar plane, P=(r,θ) directly coordinates to (x,y) in the Cartesian plane by (x,y) = (rcos(θ), rsin(θ)). So using this,

x=r\cos(\theta )

y=r\sin(\theta )

This allows translation from polar coordinates to Cartesian coordinates.

From Cartesian To Polar Coordinates

The same principles allow translation from the Cartesian plane to the polar plane. Note on the right triangles formed on the unit circle, it was determined that 1=x²+y² or when scaled by r, it was determined that $x=r\cos(\theta )$ and $y=r\sin(\theta )$ so $r^{2}=x^{2}+y^{2}$ .

This gives the radius necessary to find the corresponding (r,θ) that goes with (x,y), or the distance the point (x,y) is from the origin. Another way to think about r is using the distance formula (a derivation of the Pythagorean theorem) between the point (x,y) and (0,0). This would be $d={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}$ or $d^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}$ so plugging in (x,y) and (0,0), $d^{2}=(x-0)^{2}+(y-0)^{2}\Rightarrow d={\sqrt {(x-0)^{2}+(y-0)^{2}}}={\sqrt {x^{2}+y^{2}}}$ or $d^{2}=x^{2}+y^{2}$ where d=r.

Then it is necessary to find θ. Consider again the tan(θ) derived above. It was shown that

\tan(\theta )={\frac {\sin(\theta )}{\cos(\theta )}}

and

x=r\cos(\theta ),\;y=r\sin(\theta )

{\frac {x}{r}}=\cos(\theta ){\text{ and }}{\frac {y}{r}}=\sin(\theta )

So then $\tan(\theta )={\frac {\sin(\theta )}{\cos(\theta )}}={\frac {y/r}{x/r}}={\frac {y}{x}}$

So to solve for θ, $\theta =\tan ^{-1}\left({\frac {x}{y}}\right)$ . However, the tangent function is undefined at (0,1) and (0,-1) since cos(90°)=cos(270°) = 0, then $\tan(90^{\circ })={\tfrac {\sin(90^{\circ })}{0}}$ and $\tan(270^{\circ })={\tfrac {\sin(270^{\circ })}{0}}$ and dividing by 0 makes a function undefined. Additionally, dividing two negative numbers gives a positive number, so (-x,-y) and (x,y) would yield the same result when plugged into $\tan ^{-1}\left({\tfrac {x}{y}}\right)=\tan ^{-1}\left({\tfrac {-x}{-y}}\right)$ but the points are not at the same angle! Similarly, (-x,y) and (x,-y) are in two different locations with two different angles but similarly yield the same value in $\tan ^{-1}\left({\tfrac {-x}{y}}\right)=\tan ^{-1}\left({\tfrac {x}{-y}}\right)$ . Because of this, inverse tangent is bounded in calculators to only give angle values in the first and fourth quadrants (note: it gives negative angle values for the angles in the fourth quadrant) which are bounded by 90° and 270° and have no undefined points in between. Therefore negative inputs give a negative angle measure from the fourth quadrant and positive inputs give an angle measure from the first quadrant. To account for this, it is important to note which quadrant the point is in. If it is in quadrant 2, the calculator will take in a negative x/y ratio give a negative angle value and so it is necessary to add 180° to this. As seen in figure 12, θ and the value the calculator gives are supplementary, and since the calculator gives a negative value, it is sufficient to add 180° to the calculator value to get θ.

For a point in quadrant four, the ratio of x and y is positive, so it gives a value in quadrant 1. The value in quadrant 4 is greater than 180°, so adding 180° to the calculator output will yield a result in the fourth quadrant (figure 13). The angle given by the calculator value is a vertical angle to the size of the angle in excess of 180° (the angle defect) and therefore they have equal value, so adding the calculator value to 180° gives the total θ value.

Lastly, to correct the negative angle value given for a point in the fourth quadrant, one must simply add 360° to the value, as its positive value is represented by a counterclockwise rotation from the polar axis to that point minus the given negative angle value that would complete the rotation, 360°.

Additionally, one could make a system of equations using

x=r\cos(\theta )

y=r\sin(\theta )

To find r and θ as well by solving for r and substituting back in:

r={\frac {x}{\cos(\theta )}}

y={\frac {x}{\cos(\theta )}}\cdot \sin(\theta )=x\cdot \tan(\theta )=y

\tan(\theta )={\frac {y}{x}}

\tan ^{-1}{\frac {y}{x}}=\theta

Which is the same as the previous result, it just helps those who think algebraically. To summarize:

From Cartesian to Polar

r={\sqrt {x^{2}+y^{2}}}

\theta {\text{ in Q1}}=\tan ^{-1}{\frac {x}{y}}

\theta {\text{ in Q2}}=\tan ^{-1}{\frac {-x}{y}}+180^{\circ }

\theta {\text{ in Q3}}=\tan ^{-1}{\frac {-x}{-y}}+180^{\circ }

\theta {\text{ in Q4}}=\tan ^{-1}{\frac {x}{-y}}+360^{\circ }

From Polar to Cartesian

x=r\cos(\theta )

y=r\sin(\theta )

Relating Graphs Between the Cartesian and Polar Planes

Note: all graphs will be graphed with restriction 0≤x≤2π and 0≤θ≤2π and will be in radians A really cool graphing application with suggestions of graphs to investigate: http://home.fuse.net/clymer/graphs/polar.html

Graphing trigonometric functions in the Cartesian plane can be a little tricky. Sometimes it is hard to tell when the function should stop iterating on the restricted domain, see phase shifts, or see other various transformations and know how to graph them or even what is shown on the graph. Thankfully, polar coordinates simplify this process. Consider a graph in Cartesian coordinates. For example: $y=a\cos(kx)$

While this is able to be graphed in the Cartesian plane, it is difficult to tell visually how many iterations occur in the interval as k increases. This is a difficult topic for many students to grasp due to the symmetry of the sine and cosine functions. Polar coordinates simplify this by allowing the students to see how the graphs are limited by the interval θ is on.

The number of waves in a sin or cosine graph will be finite in the coordinate plane, represented by the rose petal graph when k>1. Here are some gif images of the functions iterating over 0≤x≤2π and how they map to the polar plane.

A quick step by step tutorial of how to do this is Geometer’s Sketchpad to further investigate

Open a new sketchpad document and click Graph > Grid form > Square
Plot a function f(x)= whatever function is desired.
Construct a point on that function. Select the point and click Measure> Abscissa and label the abscissa something other than “x”. Label the point itself “Cartesian”. For this tutorial, it will be named “y”.
In the Number menu, make a new parameter and name it “r”. The initial value can be anything. After it is created, double click “r=…” to edit its value. Change the value to f(y).
Change the grid form to polar. In order, click “r” and then “y” and click Graph > Plot as (r,θ). Label this point “Polar”.
Change the grid form back to square. Highlight the Polar point and click Display>Trace.
Select the “Cartesian” point and click Display>Animate
Play around with any function is desired by changing f(x) moving the “Cartesian” point back to 0 and erasing traces, then start the animation again.

So in the case of directly investigating trigonometric functions, the difference between polar and rectangular is that the height of the wave is determined by the distance from the x-axis, giving rectangular graphs of trigonometric functions a linear trend to their motion. This allows the functions to continue on forever, as long as the period is being expanded continually, nothing is bounding the graph (besides a y and –y value, but not in the x direction.) However, in the polar plane, the graph jumps out to its maximum height (r) at a value of θ that causes the graph to achieve this maximum value, and then returns to the origin before going to its minimum, -r, in a different direction, determined by θ. In this way, it is bounded by the trigonometry itself. Since there are a limited number of radians/degrees in a circle, eventually the function will be repeating itself (multiples of certain θ values), but it will always be growing and then being pulled back in to 0 due to the cyclic nature of trigonometric ratios, which are determined by a point traveling across a unit circle.

There are many other graphs that can be investigated besides just the rose functions. For the basic polar graph forms, go to any of the resources listed at the top of this page. Additionally, try manipulating different pieces of the equation to see how the frequency, amplitude and period change. This was not done in this section because the primary goal of this section was to show the direct connections between trigonometric functions in the Cartesian plane and in the polar plane.

Note that for r=1, as x (aka θ) increases from 0 to 2π, the polar point travels along the unit circle. This will be significant shortly.

Polar Coordinates and the Complex Plane

So consider now the complex plane, where a is the distance along the real line (the x-axis) and b is the distance along the imaginary axis (y-axis). So (a,b) = (distance along real axis in x direction, distance along imaginary axis in y direction) = (rcos(θ), rsin(θ)) where (a,b) = a+bi = rcos (θ)+rsin(θ)*i = r(cos (θ)+isin(θ)) = z (where z is any complex number).

Define f(z) to be $e^{z}$ where z=a+bi. Since $e^{x}$ is its own derivative, consider the complex case $e^{z}=e^{a+bi}=e^{a}e^{bi}$ . Using the chain rule in the case where a=0, ${\tfrac {d}{db}}\left(e^{bi}\right)=ie^{bi}$

In the complex plane, the imaginary axis is perpendicular to the real axis, so multiplying a real number b by i rotates that number 90° about the origin from the real line to the imaginary line. So then the derivative to $e^{bi}$ is perpendicular to the value at the point $e^{bi}$ so the function is changing at the exact same rate as its current value at any b. This is a quality that only circles have, so it can be inferred that $e^{bi}$ maps point to a circular path.

Trying out the point (0,0) gives $f(z)=f(a,b)=(0,0)=e^{0i}=e^{0}=1$

The radius of this circle, because the radius of a circle is constant, is 1. So it is a unit circle, which means the coordinates previously discussed describe the function $e^{a+bi}$ as well. So inputting z into f(z) gives the function $e^{a+bi}$ where $e^{a+bi}$ represents the coordinates of points along a unit circle in the complex plane since $e^{bi}$ exists at the points 1 away from (0,0) at a point on this unit circle at point (a,b), in direction b.

So $e^{a+bi}=e^{a}e^{bi}=r(\cos(\theta )+i\sin(\theta ))$ where b=θ (since b determines the direction of the point based on a rotation around the point (0,0) defined by the angle between the x axis and the radius) and $r=e^{a}$ since a is the only real value in a+bi and r is the only real part in these new coordinates as they are defined. So from this, $e^{2\pi i}=e^{0}e^{2\pi i}=1(cos(2\pi )+i\sin(2\pi ))=1$ . This is verifiable since $e^{2\pi i}$ lies on the circle formed by $e^{bi}$ which has a radius of 1.

This was written for personal use and not for profit classroom use. Please cite the page for any other use, including commercial.