Physics equations/Introduction to entropy
Quasi-proof of the existence of entropy as a state variable
[edit | edit source]Abstract:
The Clausius definition of entropy as, dS=kBdQ/T, fails to establish that entropy is a state variable until the integral of dS is shown to be path independent. The argument that entropy exists as a state variable begins with the Carnot theorem, used to establish that all reversible heat engines have the same thermodynamic efficiency. We then develop entropy for the ideal gas and use Carnot's theorem extend that result to all substances by arguing that all paths yield the same change in entropy. A subdivision of a closed path into an arbitrarily large number of small Carnot cycles illustrates the concept.
State variables
[edit | edit source]
In this essay we consider a simple thermodynamic system in which the number of particles is held fixed. This system can be usually be characterized by two state variables. These state variables include pressure (P), volume (V), energy (E), and temperature (T). It is generally understood that all state variables can be deduced from the volume and temperature: For example, one might place the piston in a heat bath of known temperature, fix the volume, and measure the pressure. Energy must be calculated, but the calculation can be verified by changing the system and monitoring how much heat energy and work is expended or released in order to achieve different values of volume and temperature.
Clausius definition of entropy
[edit | edit source]In 1862 Clausius proposed that entropy is[1][2]
- (1)
where dQ is heat transferred during a reversible process .
---Click for more on irreversible processes---> 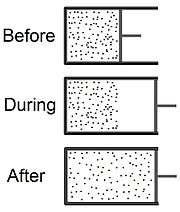
A free expansion of a gas can be achieved by moving the piston out faster than the fastest atoms in the gas. Examples of irreversible processes include systems include:
- Devices with mechanical friction present
- The sudden expansion or compression
- Heat transfer between bodies with significantly different temperature. Heat flow must occur between bodies of different temperatures (unless a heat pump is present). Reversible heat flow is an idealization that can only occur in the limit that the difference in temperature between the two bodies is zero. Consequently, this and all reversible processes must be quasi-static. [3]
Simple heat engine
[edit | edit source]
The simple heat engine described in the figure to the right operates on a cycle which appears as a rectangle when the state is described on a PV diagram (pressure versus volume). As discussed above, each point on the diagram defines all other state variables, which can be expressed on the PV diagram using contours. For example, contours of constant temperature (called isotherms) are shown in the figure. Most substances tend to lose pressure when they cool, and the figure follows this format with red isotherms indicating lower temperature at lower pressure and volume, with the blue (hot) isotherms occupying the upper right portion of the PV diagram. By the way the path crosses isotherms we see that the temperature is reduced along 2-3-4 and increases along 4-1-2. It can also be shown that:
- The work done by the engine in each cycle equals the area enclosed by the loop.
- In the course of each cycle the net amount of heat that enters the substance must equal the net amount of work done by the substance. Mathematically this can be expressed as: ΔQin = ʃdQ = ΔWout = ʃPdV.
- Neither heat, Q, nor work, W, can be state variables.
---Proof of these statements-----------> In this discussion, we let the differential, 'd', refer to a small difference, and let Δ refer to net change that occurs during one cycle of the heat engine. 1. Show that the work is ʃPdV:
Work is done by the substance if the pressure exerts a force (pressure/area) in the same direction as motion of the piston. Let the distance moved be dΔx, and change in volume be dV=Adx, where A is the area of the piston. We follow the convention that dW is negative if the substance expends internal energy by doing work:
2. Show that each time a cycle is completed,
By conservation of energy, the work done by the gas(-PΔV) plus the heat that enters(ΔQ) is equal to the change in the total energy of the system. But since the cycle returns to substance to its original state, the change in energy, ΔE, must be zero.
3. Show that neither heat, Q, nor work, W, are state variables.
Conservation of energy for this system is state as the first law of thermodynamics.
During each cycle of the heat engine, a net amount of heat, ΔQ enters the substance. If Q (heat) were a state variable, this 'heat' would progressively increase as the cycles are repeated. Likewise, if W (work) were a state variable, the substance would progressively 'lose' it's work. Heat and work describe the mechanism by which energy enters or leaves a substance. Energy can enter by one mechanism and leave by the other.
When an engine does a great deal of work after completing many cycles, the piston may become worn, atoms might escape or enter the sealed piston, or chemical reactions might occur. But the atoms themselves remain the same. At the atomic level, history is irrelevant. The same is true at the sub-atomic level. The radioactive isotope that has escaped decay for thousands years is exactly the same as one that was freshly made.
The Carnot cycle
[edit | edit source]

The Carnot engine represents an important cycle that consists of two adiabats and two isotherms:
- An adiabat is a contour where no heat flows.
- An isotherm is a contour where the temperature remains constant.
In our case, it is best to imagine the adiabatic condition as achieved by thermal insulation of the piston.(although approximate adiabatic compression of air by sound waves can also occur because the air decompresses before heat has time to exit a fluid element.)
The isothermal condition is maintained by submerging the piston into a heat reservoir (also called a heat bath). Heat flows during both isothermal stages of a Carnot cycle . Heat, by definition is the flow of energy between substances of different temperature. By the second law of thermodynamics the energy always flows from the high temperature substance and into the cooler one. The student to wonder how heat flows between substances of the same temperature. The Carnot heat engine is an idealization that can be approached only in the limit that the process is so slow that the difference in temperature between the substance and reservoir is very small. Only in this limit will a substance being made hot by compression be in equilibrium with a reservoir with a temperature that is lower by a negligibly small amount.
Carnot's theorem of thermodynamics
[edit | edit source]
In a later section, we shall establish that entropy exists as a state variable for an ideal gas. The second part of Carnot's theorem (on thermodynamics) gives us an equivalency of all reversible heat engines that will help to establish that all substances in equilibrium possess entropy. :[4]
All reversible engines operating between the same reservoirs have the same efficiency, regardless of what substance is used as the working fluid.
The efficiency, η, of a heat engine operating between two reservoirs is defined as the ratio of the work done per cycle to the amount of heat that leaves the hot temperature bath:
We shall later see that an efficiency of 1 (100%) occurs only if there is an infinite difference between the hot and cold temperatures. A premise of Carnot's theorem is that the engine is reversible, which implies that the engine can also act as a refrigerator, or 'heat pump' that consumes (requires) work in order to transfer heat from the cold to the hot reservoir.
---Click for more discussion of heat pumps-----> For devices used to transfer heat from a cold to a high temperature reservoir, the figure of merit is not efficiency ΔW/ΔQh, but the coefficient of performance (COP = ΔQc/ΔW). Note that a good engine tends to be a poor heat pump: A good engine produces a more work for a given amount of heat extracted from the reservoir at temperature Th, while a good heat pump maximizes the heat extracted from the cold reservoir for the least amount of work. It is also important to understand that the Carnot theorem applies to heat engines and pumps that are reversible, and therefore operate without an internal friction. Carnot's theorem will seem counter intuitive until these considerations are understood.
If two different substances produced cycles with different Carnot efficiency, then the cycle with more efficiency could drive the less efficient device as a heat pump. The result would be that heat flows from a cold reservoir to a hot one without any external work. This violates the second law of thermodynamics, and would permit the construction of a perpetual motion machine of the second kind. Figure 5 asserts this by showing that if the cycle with more efficiency, , drives the engine with less efficiency, , then heat would flow from the cold to the hot reservoir without the application of external work.
----Click to see the algebra that supports this ---------> For convenience we adopt the convention that all symbols, and represent non-negative quantities. We may do this provided, ). Conservation of energy demands that for each engine, the energy which enters, , must equal the energy which exits, : - ,
- ,
The figure is also consistent with the definition of efficiency as for both engines:
- ,
- .
These equations verify that the quantities of energy shown in the figure are correct. Since we have assumed, , then:
- .
In other words, the net heat flow would be backwards, i.e., into the hot reservoir:
- .
Ideal gas equations of state
[edit | edit source]
The classical ideal gas can be constructed theoretically using Boltzmann statistics, or it can be viewed as an experimentally obtained result. Here we adopt the latter approach. The concept of absolute zero arises from measuring the pressure of a gas sample as a function of temperature and noting that observed values extrapolate to zero pressure at approximately -273°C. This insight led to the Kelvin scale, which we shall use exclusively in his discussion (0 K = -273.15°C). The ideal gas law is:
- ,
where n is the number of moles, N is the number of atoms, and
- = 8.31446 J·K−1·mol−1 is the gas constant
- = 1.381 × 10−23 J·K−1 is the Boltzmann constant
Another important result that can be deduced experimentally or calculated using statistical thermodynamics is the energy of a monatomic ideal gas:
- ,
where the degrees of freedom equals:
- for a three-dimensional ideal monatomic gas.
Monatomic gases contain only on atom and include the noble gasses (He, Ar, ...). For reasons that cannot be explained without quantum mechanics, such atoms do not spin at the temperatures usually encountered in the laboratory. When developing mathematical models of the ideal gas it is convenient to first solve the problem for particles confined to a single dimension. The degrees of freedom for a monatomic ideal gas equals the number of dimensions, so that for a gas confined to a single spatial dimension.
Entropy of an ideal gas
[edit | edit source]Since two state variables can define our system, entropy must be a function of them, S = S(V,T). Taking the differential we would expect:
- .
Note that the identity,
- ,
imposes a constraint that must be satisfied if S is a state variable. If we combine the two equations of state for an ideal gas with the first law of thermodynamics, we have:
- ,
If we take the partial derivative of the first term with respect to V, and the other with respect to T we do not get the required identity:
.
This verifies, for an ideal gas, that heat is not a state variable. On the other hand, if we divide the above expression by T, we have,
which can be integrated to yield,
,
for the entropy of an ideal gas.
---Click to see the missing steps---> Since S is a function of two variables, we integrate with respect to one variable at a time, each time treating the other as a constant. Retain the constants of integration for both integrals, but keep in mind that one variable integrated, the constant may be a function of the other variable. Let (a function of V) be the constant when T is the variable, and let (a function of T) be the variable with V is the variable of integration: If this integration can be performed to find S=S(V,T), then it is possible to express this function so that both equations are satisfied. In this case, we satisfy both equations if:
Hence BOTH of these two equations are satisfied if .
Ideal gas Carnot cycle
[edit | edit source]
The knowledge that entropy is a state variable greatly simplifies the discussion of the Carnot cycle. Our discussion must remain confined to ideal gasses because we have not yet established entropy, S, to be a state variable for all substances. Following Wikipedia[5] we analyze the Carnot cycle using entropy and temperate as state variables. In this TS space (temperature-entropy) the Carnot cycle takes on a rectangular shape with the isotherms (ΔT=0) being two horizontal line segments, while the adiabats (ΔQ=TΔS=0) are the two vertical sides.
Application of TS diagram to substances other than ideal gasses: Although the TS diagram applies to Carnot cycles using any substance as the working fluid, it would be an act of circular reasoning to utilize it for any substance other than the ideal gas in a proof that entropy is a state variable. We shall see that this is not a serious obstacle.
Define the following as positive quantities that pertain to each cycle of the heat engine:
- = heat that enters the engine at high temperature.
- = heat that exits the engine at the low temperature.
- = work done (equal to the net heat flow because energy is conserved and because the system returns to its initial state at the end of each cycle).
This leads to an important expression for efficiency, , of the Carnot cycle:
- = = .
By Carnot's theorem, this equation holds for all reversible heat engines that operate between two temperatures.
Proof that entropy is a state variable for all substances
[edit | edit source]
Entropy is a state variable for any substance for which
for all possible closed curves on a P-V diagram, provided the path is taken under reversible conditions. The previous section already establishes that for any closed curve that is a Carnot cycle,
- ,
which implies that and are equal and opposite, which establishes that entropy is conserved for any (reversible) loop shaped like a Carnot cycle. The figure to the right shows how any path from point 1 to point 2 on a P-V diagram can be deformed into any other path without changing the value of . To accomplish this, subdivide the area between the two paths into an arbitrarily large number of 'small' Carnot cycles. Since for all such 'small' Carnot cycles, one can transform one path into the other one Carnot cycle at a time.
There are some caveats to this argument:
- The entire region inside the space between the two curves must be accessible (see contour integrals in complex analysis).
- As with a number of devices constructed in this argument, it is physically impossible to perform this experiment.
- The theorem does not apply to smooth paths, but only to those that are sawtooth with changes in P alternating with changes in V. A calculation of path length using such methods would yield the wrong answer: For path integrals in x-y space .
It is blemishes like these that suggest that all "proofs" in physics are actually quasiproofs.
References
[edit | edit source]- ↑ https://en.wikipedia.org/w/index.php?title=Clausius_theorem&oldid=560729049
- ↑ https://en.wikipedia.org/w/index.php?title=Entropy&oldid=584258991
- ↑ https://en.wikipedia.org/w/index.php?title=Quasistatic_process&oldid=584998431
- ↑ https://en.wikipedia.org/w/index.php?title=Carnot%27s_theorem_%28thermodynamics%29&oldid=588223008
- ↑ https://en.wikipedia.org/w/index.php?title=Carnot_cycle&oldid=585407209























































