Nonlinear finite elements/Updated Lagrangian formulation

Updated Lagrangian formulation

We will now derive the finite element equations for the updated Lagrangian formulation for three-dimensional problems in solid mechanics.

Updated Lagrangian governing equations

The updated Lagrangian equations are

${\begin{aligned}\rho _{0}(\mathbf {X} )&=J(\mathbf {X} ,t)~\rho (\mathbf {X} ,t)\\\rho ~{\dot {\mathbf {v} }}&={\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}^{T}+\rho ~\mathbf {b} \\{\boldsymbol {\sigma }}&={\boldsymbol {\sigma }}^{T}\\\rho ~{\dot {e}}&={\boldsymbol {\sigma }}:{\boldsymbol {d}}-{\boldsymbol {\nabla }}\cdot \mathbf {q} +\rho ~s\\{\mathcal {L}}_{\varphi }~{\boldsymbol {\sigma }}&={\boldsymbol {G}}({\boldsymbol {\sigma }},{\boldsymbol {d}},T,\dots )\\{\boldsymbol {d}}&={\frac {1}{2}}({\boldsymbol {l}}+{\boldsymbol {l}}^{T})\end{aligned}}$

The boundary conditions are

${\begin{aligned}{\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} &=\mathbf {t} \qquad {\text{on}}~~\partial \Omega _{t}\\\mathbf {v} &={\overline {\mathbf {v} }}\qquad {\text{on}}~~\partial \Omega _{v}\end{aligned}}$

The initial conditions are

${\begin{aligned}\mathbf {v} (\mathbf {X} ,0)&=\mathbf {v} _{0}(\mathbf {X} )\\{\boldsymbol {\sigma }}(\mathbf {X} ,0)&={\boldsymbol {\sigma }}_{0}(\mathbf {X} )\qquad {\text{or}}\qquad \mathbf {u} (\mathbf {X} ,0)&=\mathbf {u} _{0}(\mathbf {X} )\end{aligned}}$

Dependent variables

Note that the dependent variables in this case are all expressed as functions of the Lagrangian (material) coordinates, i.e.,

1. Velocity ($\mathbf {v} (\mathbf {X} ,t)$)
2. Cauchy stress (${\boldsymbol {\sigma }}(\mathbf {X} ,t)$)
3. Rate of deformation (${\boldsymbol {d}}(\mathbf {v} ,t)$)

Also note that instead of ${\boldsymbol {\sigma }}$ and ${\boldsymbol {d}}$, we may use ${\boldsymbol {S}}$ and ${\boldsymbol {E}}$ in our calculations and then transform to ${\boldsymbol {\sigma }}$.

Weak form of the balance of linear momentum

Another name for the weak form is the Principle of Virtual Power (or Principle of Virtual Work if rates are not involved).

The strong form consists of the balance of linear momentum and the traction boundary conditions. That is,

${\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}^{T}+\rho ~\mathbf {b} &=\rho ~\mathbf {a} \qquad {\text{in}}~~\Omega \\{\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} &=\mathbf {t} \qquad {\text{on}}~~\partial \Omega _{t}\end{aligned}}$

where $\mathbf {a} ={\dot {\mathbf {v} }}={\ddot {\mathbf {u} }}$ is the acceleration.

The weak form of this equation can be written as

${\int _{\Omega }\rho ~\mathbf {a} \cdot \mathbf {w} ~{\text{dV}}+\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\mathbf {w} )~{\text{dV}}=\int _{\Omega }\rho ~\mathbf {b} \cdot \mathbf {w} ~{\text{dV}}+{\int _{\partial \Omega }}_{t}\mathbf {t} \cdot \mathbf {w} ~{\text{dA}}}$

where $\mathbf {w}$ is a vector valued weighting function (also called a test function) that is zero at the points on the boundary where the essential boundary conditions on $\mathbf {v}$ are applied. Therefore we can think of $\mathbf {w}$ as a variation of $\mathbf {v}$.

Derivation of the weak form

We proceed in the usual manner to derive the weak form. We multiply the differential equation with the weighting function and integrate over the volume to get

$\int _{\Omega }\mathbf {w} \cdot \left({\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}^{T}+\rho ~\mathbf {b} -\rho ~\mathbf {a} \right)~{\text{dV}}=0$

Using the identity

${\boldsymbol {\nabla }}\cdot ({\boldsymbol {A}}^{T}\cdot \mathbf {b} )=\mathbf {b} \cdot ({\boldsymbol {\nabla }}\cdot {\boldsymbol {A}})+{\boldsymbol {A}}:({\boldsymbol {\nabla }}\mathbf {b} )$

and noting that ${\boldsymbol {\sigma }}={\boldsymbol {\sigma }}^{T}$ (conservation of angular momentum), we have

$\int _{\Omega }\mathbf {w} \cdot ({\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}^{T})~{\text{dV}}=\int _{\Omega }{\boldsymbol {\nabla }}\cdot ({\boldsymbol {\sigma }}\cdot \mathbf {w} )~{\text{dV}}-\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\mathbf {w} )~{\text{dV}}$

From the divergence theorem we have

$\int _{\Omega }{\boldsymbol {\nabla }}\cdot ({\boldsymbol {\sigma }}\cdot \mathbf {w} )~{\text{dV}}=\int _{\partial \Omega }\mathbf {n} \cdot ({\boldsymbol {\sigma }}\cdot \mathbf {w} )~{\text{dA}}$

where $\mathbf {n}$ is the outward unit normal to the boundary. So,

$\int _{\Omega }\mathbf {w} \cdot ({\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }})~{\text{dV}}=\int _{\partial \Omega }\mathbf {n} \cdot ({\boldsymbol {\sigma }}\cdot \mathbf {w} )~{\text{dA}}-\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\mathbf {w} )~{\text{dV}}$

Now, on the boundary

$\mathbf {n} \cdot ({\boldsymbol {\sigma }}\cdot \mathbf {w} )\equiv n_{i}~\sigma _{ij}~w_{j}=\sigma _{ji}~n_{i}~w_{j}\equiv ({\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} )\cdot \mathbf {w} =\mathbf {t} \cdot \mathbf {w}$

On the part of the boundary where no tractions are applied, we have $\mathbf {t} =\mathbf {0}$ and hence $\mathbf {n} \cdot ({\boldsymbol {\sigma }}\cdot \mathbf {w} )=\mathbf {0}$. Therefore we can write

$\int _{\Omega }\mathbf {w} \cdot ({\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }})~{\text{dV}}={\int _{\partial \Omega }}_{t}\mathbf {t} \cdot \mathbf {w} ~{\text{dA}}-\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\mathbf {w} )~{\text{dV}}$

where $\partial \Omega _{t}$ is the part of the boundary where the tractions are applied.

Plugging this expression into the weighted average form of the balance of linear momentum we get

${\int _{\partial \Omega }}_{t}\mathbf {t} \cdot \mathbf {w} ~{\text{dA}}-\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\mathbf {w} )~{\text{dV}}+\int _{\Omega }\mathbf {w} \cdot \left(\rho ~\mathbf {b} -\rho ~\mathbf {a} \right)~{\text{dV}}=0$

Rearranging terms we get the required weak form

$\int _{\Omega }\rho ~\mathbf {a} \cdot \mathbf {w} ~{\text{dV}}+\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\mathbf {w} )~{\text{dV}}=\int _{\Omega }\rho ~\mathbf {b} \cdot \mathbf {w} ~{\text{dV}}+{\int _{\partial \Omega }}_{t}\mathbf {t} \cdot \mathbf {w} ~{\text{dA}}$

Physical interpretation of terms

To provide a physical interpretation of the four terms in the weak form, we write the weighting function as a variation of the velocity, i.e., $\mathbf {w} =\delta \mathbf {v}$. Then we have the familiar principle of virtual power:

$\int _{\Omega }\rho ~\mathbf {a} \cdot \delta \mathbf {v} ~{\text{dV}}+\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\delta \mathbf {v} )~{\text{dV}}=\int _{\Omega }\rho ~\mathbf {b} \cdot \delta \mathbf {v} ~{\text{dV}}+{\int _{\partial \Omega }}_{t}\mathbf {t} \cdot \delta \mathbf {v} ~{\text{dA}}$

The first term on the left can then be identified as the virtual kinetic power, the second term on the left as the virtual internal power, and the sum of the two terms on the right as the virtual external power. In other words, we have

${\begin{aligned}\delta P_{\text{kin}}&:=\int _{\Omega }\rho ~\mathbf {a} \cdot \delta \mathbf {v} ~{\text{dV}}\\\delta P_{\text{int}}&:=\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\delta \mathbf {v} )~{\text{dV}}\\\delta P_{\text{ext}}&:=\int _{\Omega }\rho ~\mathbf {b} \cdot \delta \mathbf {v} ~{\text{dV}}+{\int _{\partial \Omega }}_{t}\mathbf {t} \cdot \delta \mathbf {v} ~{\text{dA}}\end{aligned}}$

and

$\delta P_{\text{kin}}+\delta P_{\text{int}}=\delta P_{\text{ext}}~.$

We can see why the second terms is identified as the virtual internal power as follows. Note that

${\boldsymbol {\nabla }}\delta \mathbf {v} =\delta {\boldsymbol {l}}=\delta ({\boldsymbol {d}}+{\boldsymbol {w}})$

where ${\boldsymbol {l}}$ is the velocity gradient, ${\boldsymbol {d}}$ is symmetric rate of deformation tensor, and ${\boldsymbol {w}}$ is the skew symmetric spin tensor. Therefore, since the product of a symmetric and a skew symmetric tensor is zero, we have

${\boldsymbol {\sigma }}:{\boldsymbol {\nabla }}\delta \mathbf {v} ={\boldsymbol {\sigma }}:\delta {\boldsymbol {d}}+{\boldsymbol {\sigma }}:\delta {\boldsymbol {w}}={\boldsymbol {\sigma }}:\delta {\boldsymbol {d}}$

Hence,

$\delta P_{\text{int}}=\int _{\Omega }{\boldsymbol {\sigma }}:\delta {\boldsymbol {d}}~{\text{dV}}$

This has the same form as the expression for internal power that we discussed earlier.

Finite element discretization

Let us go back to the original weak form that we derived, i.e.,

$\int _{\Omega }\rho ~\mathbf {a} \cdot \mathbf {w} ~{\text{dV}}+\int _{\Omega }{\boldsymbol {\sigma }}:({\boldsymbol {\nabla }}\mathbf {w} )~{\text{dV}}=\int _{\Omega }\rho ~\mathbf {b} \cdot \mathbf {w} ~{\text{dV}}+{\int _{\partial \Omega }}_{t}\mathbf {t} \cdot \mathbf {w} ~{\text{dA}}$

Trial function

To start the discretization process we have to first choose an approximate solution $\mathbf {v} _{h}$ from the space ${\mathcal {S}}_{h}$ of admissible finite element trial functions. These functions must satisfy at least $C^{0}$ continuity and the essential boundary condition $\mathbf {v} ={\overline {\mathbf {v} }}$ on ${\partial \Omega }_{v}$.

More formally, we choose $\mathbf {v} _{h}(\mathbf {X} ,t)\in {\mathcal {S}}_{h}$ where

${\mathcal {S}}_{h}=\{\mathbf {v} ~|~\mathbf {v} \in C^{0}(\mathbf {X} ),~~\mathbf {v} ={\overline {\mathbf {v} }}~{\text{on}}~\partial \Omega _{v}\}$

If we discretize the body into a number of elements with $n$ nodes, then we can write the approximate solution as

$\mathbf {v} _{h}(\mathbf {X} ,t)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\mathbf {v} _{I}(t)$

The quantities $N_{I}(\mathbf {X} )$ are the shape functions which provide the required level of continuity and are chosen so that $\mathbf {v} _{h}\in {\mathcal {S}}_{h}$.

Test function

We also have to choose appropriate weighting functions ($\mathbf {w} _{h}$) which are also known as test functions.

In Galerkin finite elements we choose these functions from the same space as the trial functions with the additional restriction that these functions go to zero at points on the boundary where essential boundary conditions are applied.

Formally, choose $\mathbf {w} _{h}(\mathbf {X} )\in {\mathcal {S}}_{t}$ where

${\mathcal {S}}_{t}=\{\mathbf {w} ~|~\mathbf {w} \in C^{0}(\mathbf {X} ),~~\mathbf {w} =\mathbf {0} ~{\text{on}}~\partial \Omega _{v}\}$

For finite element analysis, these weighting functions have the same form as the trial function, i.e.,

$\mathbf {w} _{h}(\mathbf {X} )=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\mathbf {w} _{I}$

Motion

Instead of a trial function for the velocity, we can start with one for the motion and then take time derivatives. In this case, we choose the motion to be approximated by

$\mathbf {x} _{h}(\mathbf {X} ,t)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\mathbf {x} _{I}(t)$

where $N_{I}(\mathbf {X} )$ are the nodal shape functions (note that these are functions of $\mathbf {X}$) and $\mathbf {x} _{I}(t)$ are the positions of nodes $i$ in the current configuration. Therefore, nodes remain coincident with material point labels at all times.

Therefore, in the reference configuration, we have

$\mathbf {x} _{h}(\mathbf {X} ,0)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\mathbf {x} _{I}(0)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\mathbf {X} _{I}$

The shape functions are also chosen such that

$N_{I}(\mathbf {X} _{J})=\delta _{IJ}$

Then the displacement $\mathbf {u} =\mathbf {x} -\mathbf {X}$ can be approximated by

$\mathbf {u} _{h}(\mathbf {X} ,t)=\mathbf {x} _{h}(\mathbf {X} ,t)-\mathbf {X} _{h}=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\left[\mathbf {x} _{I}(t)-\mathbf {X} _{I}\right]=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\mathbf {u} _{I}(t)$

The velocity $\mathbf {v}$ is given by the time derivative of $\mathbf {u}$ keeping $\mathbf {X}$ fixed. So we have

$\mathbf {v} _{h}(\mathbf {X} ,t)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~{\dot {\mathbf {u} }}_{I}(t)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\mathbf {v} _{I}(t)$

Note that this approximation has the same form as the trial function for the velocity that we started with.

The acceleration $\mathbf {a}$ is given by the time derivative of $\mathbf {v}$. Hence

$\mathbf {a} _{h}(\mathbf {X} ,t)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~{\ddot {\mathbf {u} }}_{I}(t)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~{\dot {\mathbf {v} }}_{I}(t)=\sum _{I=1}^{n}N_{I}(\mathbf {X} )~\mathbf {a} _{I}(t)$

Velocity gradient and rate of deformation

The spatial velocity gradient ${\boldsymbol {l}}$ is given by

${\boldsymbol {l}}(\mathbf {x} ,t)={\boldsymbol {\nabla }}\mathbf {v} (\mathbf {x} ,t)$

Note that the derivatives are with respect to $\mathbf {x}$ and not $\mathbf {X}$.

Therefore, the approximation that we seek has the form

${\boldsymbol {l}}_{h}(\mathbf {x} ,t)=\sum _{I=1}^{n}{\boldsymbol {\nabla }}[N_{I}(\mathbf {X} )~\mathbf {v} _{I}(t)]$

Using the identity

${\boldsymbol {\nabla }}(\varphi ~\mathbf {a} )=\mathbf {a} \otimes ({\boldsymbol {\nabla }}\varphi )+\varphi ~{\boldsymbol {\nabla }}\mathbf {a}$

we get

${\boldsymbol {l}}_{h}(\mathbf {x} ,t)=\sum _{I=1}^{n}\mathbf {v} _{I}(t)\otimes {\boldsymbol {\nabla }}N_{I}(\mathbf {X} )$

In index notation,

$[l_{ij}]_{h}=\sum _{I=1}^{n}v_{Ii}~{\frac {\partial N_{I}(\mathbf {X} ,t)}{\partial x_{j}}}=v_{Ii}~N_{I,j}$

The rate of deformation is then given by

${\boldsymbol {d}}_{h}(\mathbf {x} ,t)={\frac {1}{2}}~\left({\boldsymbol {l}}_{h}+{\boldsymbol {l}}_{h}^{T}\right)=\sum _{I=1}^{n}{\frac {1}{2}}\left[\mathbf {v} _{I}(t)\otimes {\boldsymbol {\nabla }}N_{I}(\mathbf {X} )+{\boldsymbol {\nabla }}N_{I}(\mathbf {X} )\otimes \mathbf {v} _{I}(t)\right]$

In index notation,

$[d_{ij}]_{h}=\sum _{I=1}^{n}{\frac {1}{2}}[v_{Ii}~N_{I,j}+v_{Ij}~N_{I,i}]$

Approximate weak form

We can now substitute the trial and test functions into the weak form of the momentum equation to get (using the same procedure as in one-dimension)

${\int _{\Omega }\rho ~N_{I}~\mathbf {a} _{h}~{\text{dV}}+\int _{\Omega }{\boldsymbol {\sigma }}\cdot ({\boldsymbol {\nabla }}N_{I})~{\text{dV}}=\int _{\Omega }\rho ~N_{I}~\mathbf {b} ~{\text{dV}}+{\int _{\partial \Omega }}_{t}N_{I}~\mathbf {t} ~{\text{dA}}}$

We can write this approximate weak form as

$\mathbf {f} _{I}^{\text{kin}}+\mathbf {f} _{I}^{\text{int}}=\mathbf {f} _{I}^{\text{ext}}$

where the first term represents the inertial force, the second term the internal force, and the third term the external force. Thus,

${\begin{aligned}\mathbf {f} _{I}^{\text{kin}}&:=\int _{\Omega }\rho ~N_{I}~\mathbf {a} _{h}~{\text{dV}}\\\mathbf {f} _{I}^{\text{int}}&:=\int _{\Omega }{\boldsymbol {\sigma }}\cdot ({\boldsymbol {\nabla }}N_{I})~{\text{dV}}\\\mathbf {f} _{I}^{\text{ext}}&:=\int _{\Omega }\rho ~N_{I}~\mathbf {b} ~{\text{dV}}+{\int _{\partial \Omega }}_{t}N_{I}~\mathbf {t} ~{\text{dA}}\end{aligned}}$

The mass matrix

The term

$\mathbf {f} _{I}^{\text{kin}}:=\int _{\Omega }\rho ~N_{I}~\mathbf {a} _{h}~{\text{dV}}$

is the inertial force term.

If we substitute

$\mathbf {a} (\mathbf {X} ,t)=\sum _{J=1}^{n}N_{J}(\mathbf {X} )~\mathbf {a} _{J}(t)$

into the inertial force terms, we get

$\mathbf {f} _{I}^{\text{kin}}=\sum _{J=1}^{n}\left[\int _{\Omega }\rho ~N_{I}~N_{J}~{\text{dV}}\right]~\mathbf {a} _{J}$

We define the mass matrix as the quantity

${M_{IJ}:=\int _{\Omega }\rho ~N_{I}~N_{J}~{\text{dV}}=\int _{\Omega _{0}}\rho _{0}~N_{I}~N_{J}~{\text{dV}}_{0}}$

Therefore, the inertial force can be expressed, in analogy with Newton's second law, as

$\mathbf {f} _{I}^{\text{kin}}=\sum _{J=1}^{n}M_{IJ}~\mathbf {a} _{J}$

Semi-discrete finite element equations

We can then write the semi-discrete version of the weak form in the shape of a matrix equation as

$[\mathbf {M} ][\mathbf {a} ]=[\mathbf {f} ^{\text{ext}}]-[\mathbf {f} ^{\text{int}}]$

These equations are ordinary differential equations because we still have time derivatives on the left hand side - hence the system of equations is semi-discrete.

There are a number of ways in which the discretization in time can be effected. Some common approaches are the generalized midpoint rule, the Newmark $\beta$ method, or Runge-Kutta explicit integration schemes. There is a large literature on the best way of doing the discretization in time with the goal of conserving both momentum and energy as accurately as possible.

Taking derivatives and calculating integrals

At this stage we are faced with the problem of calculating derivatives and integrals with respect to $\mathbf {x}$ of quantities that depend on $\mathbf {X}$. How can we proceed?

The standard way of resolving this issue is to do all our calculations with respect to a parent element and then map the results to the reference or current configurations as necessary.

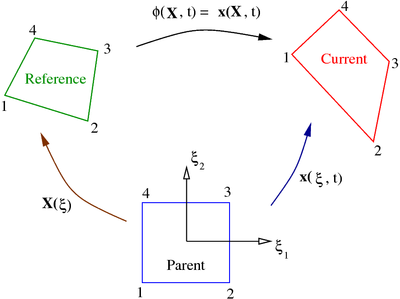
To make things more concrete let us consider a single element and label the three domains as

1. Parent element ($\square$).
2. Reference element ($\Omega _{0}$).
3. Current element ($\Omega$).

Let the maps that we need be

1. Parent $\rightarrow$ Reference : $\mathbf {X} =\mathbf {X} ({\boldsymbol {\xi }})=\mathbf {x} ({\boldsymbol {\xi }},0)$.
2. Parent $\rightarrow$ Current : $\mathbf {x} =\mathbf {x} ({\boldsymbol {\xi }},t)$.
3. Reference $\rightarrow$ Current : $\mathbf {x} =\mathbf {x} (\mathbf {X} ,t)$.

This situation is illustrated (for a two dimensional situation) in the following figure.

Maps from parent element to reference and current configurations

We define the map between the parent element and the element in the current configuration as

$\mathbf {x} ({\boldsymbol {\xi }},t)=\sum _{I}N_{I}({\boldsymbol {\xi }})~\mathbf {x} _{I}(t)$

Then,

$\mathbf {v} ({\boldsymbol {\xi }},t)=\sum _{I}N_{I}({\boldsymbol {\xi }})~\mathbf {v} _{I}(t)$

Let us now try to compute the spatial velocity gradient. We have

${\frac {\partial \mathbf {v} (\mathbf {x} ,t)}{\partial {\boldsymbol {\xi }}}}={\frac {\partial \mathbf {v} }{\partial \mathbf {x} }}\cdot {\frac {\partial \mathbf {x} }{\partial {\boldsymbol {\xi }}}}={\frac {\partial \mathbf {v} }{\partial \mathbf {x} }}\cdot {\boldsymbol {F}}_{\xi }$

The quantity

${\boldsymbol {F}}_{\xi }:={\frac {\partial \mathbf {x} }{\partial {\boldsymbol {\xi }}}}=\sum _{I}\mathbf {x} _{I}\otimes {\frac {\partial N_{I}}{\partial {\boldsymbol {\xi }}}}$

is called the Jacobian of the motion and is a function of time.

Inverting, we get

${{\frac {\partial \mathbf {v} }{\partial \mathbf {x} }}={\frac {\partial \mathbf {v} }{\partial {\boldsymbol {\xi }}}}\cdot {\boldsymbol {F}}_{\xi }^{-1}}$

But the spatial velocity gradient is

${\boldsymbol {l}}={\frac {\partial \mathbf {v} }{\partial \mathbf {x} }}$

Therefore,

${\boldsymbol {l}}={\frac {\partial \mathbf {v} }{\partial {\boldsymbol {\xi }}}}\cdot {\boldsymbol {F}}_{\xi }^{-1}$

If we substitute the approximation

$\mathbf {v} ({\boldsymbol {\xi }},t)=\sum _{I}N_{I}({\boldsymbol {\xi }})~\mathbf {v} _{I}(t)$

we get a formula for the velocity gradient

${{\boldsymbol {l}}=\left[\sum _{I}\mathbf {v} _{I}\otimes {\frac {\partial N_{I}}{\partial {\boldsymbol {\xi }}}}\right]\cdot {\boldsymbol {F}}_{\xi }^{-1}}$

A similar procedure can be followed when other spatial gradients need to be calculated. The most frequently encountered situation is the calculation of the gradient of the shape functions. In that case, we have

${{\boldsymbol {\nabla }}N_{I}(\mathbf {X} )={\frac {\partial N_{I}(\mathbf {X} )}{\partial \mathbf {x} }}={\frac {\partial N_{I}}{\partial {\boldsymbol {\xi }}}}\cdot {\boldsymbol {F}}_{\xi }^{-1}}$

For computing integrals, we observe that for a function $f(\mathbf {x} )$ on $\Omega$ we can write

$\int _{\Omega }f(\mathbf {x} )~{\text{dV}}=\int _{\Omega _{0}}{\hat {f}}(\mathbf {X} )~J~{\text{dV}}_{0}=\int _{\square }{\tilde {f}}({\boldsymbol {\xi }})~J_{\xi }~{\text{d}}\square$

where

$J_{\xi }=\det \left({\frac {\partial \mathbf {x} }{\partial {\boldsymbol {\xi }}}}\right)=\det({\boldsymbol {F}}_{\xi })$

Similarly for a function $g(\mathbf {X} )$ over $\Omega _{0}$, we have

$\int _{\Omega _{0}}g(\mathbf {X} )~{\text{dV}}_{0}=\int _{\square }{\tilde {g}}({\boldsymbol {\xi }})~J_{\xi }^{0}~{\text{d}}\square$

where

$J_{\xi }^{0}=\det \left({\frac {\partial \mathbf {X} }{\partial {\boldsymbol {\xi }}}}\right)=\det({\boldsymbol {F}}_{\xi }^{0})$

Recall that the internal force terms have the form

$\mathbf {f} _{I}^{\text{int}}=\int _{\Omega }{\boldsymbol {\sigma }}\cdot ({\boldsymbol {\nabla }}N_{I})~{\text{dV}}$

Expressed in terms of an integral over the parent element, we then have

${\mathbf {f} _{I}^{\text{int}}=\int _{\square }{\boldsymbol {\sigma }}\cdot ({\boldsymbol {\nabla }}N_{I})~J_{\xi }{\text{d}}\square }$

where

${\boldsymbol {\nabla }}N_{I}={\frac {\partial N_{I}}{\partial {\boldsymbol {\xi }}}}\cdot {\boldsymbol {F}}_{\xi }^{-1}~.$

Finite element implementation

Recall that the finite element system of equations can be written as

$[\mathbf {M} ][\mathbf {a} ]=[\mathbf {f} ^{\text{ext}}]-[\mathbf {f} ^{\text{int}}]$

where

$M_{IJ}=\int _{\Omega _{0}}\rho _{0}~N_{I}~N_{J}~{\text{dV}}_{0}~;~~\mathbf {f} _{I}^{\text{int}}=\int _{\Omega }{\boldsymbol {\sigma }}\cdot ({\boldsymbol {\nabla }}N_{I})~{\text{dV}}~;~~{\text{and}}~~\mathbf {f} _{I}^{\text{ext}}=\int _{\Omega }\rho ~N_{I}~\mathbf {b} ~{\text{dV}}+{\int _{\partial \Omega }}_{t}N_{I}~\mathbf {t} ~{\text{dA}}$

To get a feel for the structure of the equation, let us consider a four-noded plane element. If the components of the velocity in the two coordinate directions are $(u,v)$, the acceleration vector has the form

$\mathbf {a} ={\begin{bmatrix}\mathbf {a} _{1}\\\mathbf {a} _{2}\\\mathbf {a} _{3}\\\mathbf {a} _{4}\end{bmatrix}}={\begin{bmatrix}{\dot {u}}_{1}&{\dot {v}}_{1}\\{\dot {u}}_{2}&{\dot {v}}_{2}\\{\dot {u}}_{3}&{\dot {v}}_{3}\\{\dot {u}}_{4}&{\dot {v}}_{4}\end{bmatrix}}$

The mass matrix has the form

$\mathbf {M} ={\begin{bmatrix}\mathbf {M} _{11}&\mathbf {M} _{12}&\mathbf {M} _{13}&\mathbf {M} _{14}\\\mathbf {M} _{21}&\mathbf {M} _{22}&\mathbf {M} _{23}&\mathbf {M} _{24}\\\mathbf {M} _{31}&\mathbf {M} _{32}&\mathbf {M} _{33}&\mathbf {M} _{34}\\\mathbf {M} _{41}&\mathbf {M} _{42}&\mathbf {M} _{43}&\mathbf {M} _{44}\end{bmatrix}}$

In expanded form

$\mathbf {M} =\int _{\Omega _{0}}\rho _{0}~{\begin{bmatrix}N_{1}~N_{1}&N_{1}~N_{2}&N_{1}~N_{3}&N_{1}~N_{4}\\N_{2}~N_{1}&N_{2}~N_{2}&N_{2}~N_{3}&N_{2}~N_{4}\\N_{3}~N_{1}&N_{3}~N_{2}&N_{3}~N_{3}&N_{3}~N_{4}\\N_{4}~N_{1}&N_{4}~N_{2}&N_{4}~N_{3}&N_{4}~N_{4}\end{bmatrix}}~{\text{dV}}$

Next, we consider the internal force term. Let the components of the internal force in the two coordinate directions be ($f,g$). Then,

$\mathbf {f} ^{\text{int}}={\begin{bmatrix}\mathbf {f} _{1}^{\text{int}}\\\mathbf {f} _{2}^{\text{int}}\\\mathbf {f} _{3}^{\text{int}}\\\mathbf {f} _{4}^{\text{int}}\end{bmatrix}}={\begin{bmatrix}f_{1}&g_{1}\\f_{2}&g_{2}\\f_{3}&g_{3}\\f_{4}&g_{4}\end{bmatrix}}$

At this stage, recall that the velocity gradient is given by

${\boldsymbol {l}}={\boldsymbol {\nabla }}\mathbf {v} =\sum _{I}\mathbf {v} _{I}\otimes {\boldsymbol {\nabla }}N_{I}=\sum _{I}\mathbf {v} _{I}\otimes {\frac {\partial N_{I}}{\partial \mathbf {x} }}$

In index notation,

$l_{ij}=\sum _{I}v_{Ii}~{\frac {\partial N_{I}}{\partial x_{j}}}~.$

We define

$B_{Ij}:={\frac {\partial N_{I}}{\partial x_{j}}}$

Then,

$l_{ij}=\sum _{I}v_{Ii}~B_{Ij}$

In matrix form

$\mathbf {l} ={\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\mathbf {v} _{3}&\mathbf {v} _{4}\end{bmatrix}}{\begin{bmatrix}\mathbf {B} _{1}\\\mathbf {B} _{2}\\\mathbf {B} _{3}\\\mathbf {B} _{4}\end{bmatrix}}$

Expanded out

${\begin{bmatrix}l_{11}&l_{12}\\l_{21}&l_{22}\end{bmatrix}}={\begin{bmatrix}u_{1}&u_{2}&u_{3}&u_{4}\\v_{1}&v_{2}&v_{3}&v_{4}\end{bmatrix}}{\begin{bmatrix}{\frac {\partial N_{1}}{\partial x}}&{\frac {\partial N_{1}}{\partial y}}\\{\frac {\partial N_{2}}{\partial x}}&{\frac {\partial N_{2}}{\partial y}}\\{\frac {\partial N_{3}}{\partial x}}&{\frac {\partial N_{3}}{\partial y}}\\{\frac {\partial N_{4}}{\partial x}}&{\frac {\partial N_{4}}{\partial y}}\end{bmatrix}}$

In more compact form, we can just write

${[\mathbf {l} ]=[\mathbf {v} ]^{T}~[\mathbf {B} ]}$

Similarly, for the internal force term,

$\mathbf {f} _{I}^{\text{int}}=\int _{\Omega }{\boldsymbol {\sigma }}\cdot {\boldsymbol {\nabla }}N_{I}~{\text{dV}}$

we have

$f_{Ii}^{\text{int}}=\int _{\Omega }\sigma _{ij}~{\frac {\partial N_{I}}{\partial x_{j}}}~{\text{dV}}=\int _{\Omega }\sigma _{ij}~B_{Ij}~{\text{dV}}$

In matrix form,

${\begin{bmatrix}\mathbf {f} _{1}^{\text{int}}\\\mathbf {f} _{2}^{\text{int}}\\\mathbf {f} _{3}^{\text{int}}\\\mathbf {f} _{4}^{\text{int}}\end{bmatrix}}=\int _{\Omega }{\begin{bmatrix}\mathbf {B} _{1}\\\mathbf {B} _{2}\\\mathbf {B} _{3}\\\mathbf {B} _{4}\end{bmatrix}}~{\boldsymbol {\sigma }}^{T}$

Expanded out,

${\begin{bmatrix}f_{1}&g_{1}\\f_{2}&g_{2}\\f_{3}&g_{3}\\f_{4}&g_{4}\end{bmatrix}}=\int _{\Omega }{\begin{bmatrix}{\frac {\partial N_{1}}{\partial x}}&{\frac {\partial N_{1}}{\partial y}}\\{\frac {\partial N_{2}}{\partial x}}&{\frac {\partial N_{2}}{\partial y}}\\{\frac {\partial N_{3}}{\partial x}}&{\frac {\partial N_{3}}{\partial y}}\\{\frac {\partial N_{4}}{\partial x}}&{\frac {\partial N_{4}}{\partial y}}\end{bmatrix}}{\begin{bmatrix}\sigma _{11}&\sigma _{21}\\\sigma _{12}&\sigma _{22}\end{bmatrix}}~{\text{dV}}$

In compact form, we have

${[\mathbf {f} ^{\text{int}}]=\int _{\Omega }[\mathbf {B} ][{\boldsymbol {\sigma }}]^{T}~{\text{dV}}}$

We can express the external force term in a similar manner. Notice that we are not taking adavantage of the symmetry of the stress tensor in the above expressions.

A widely used alternative way of expressing the finite element system of equations is the Voigt notation. This notation can be found in discussions of introductory finite element analysis.

Algorithm for computing internal forces

The major complications and computational effort in the finite element implementation are encountered during the computation of internal forces.

The basic procedure for computing the internal force at the nodes of an element is given below.

1. Set $[\mathbf {f} ^{\text{int}}]=[\mathbf {0} ]$.
2. For all quadrature points in the parent element (${\boldsymbol {\xi }}_{Q}$)
   1. Compute the gradient of the shape functions ($[\mathbf {B} _{I}]$) for all nodes $I$.
   2. Compute the velocity gradient $[\mathbf {l} ]=[\mathbf {v} _{I}][\mathbf {B} ]$.
   3. Compute the rate of deformation tensor.
   4. Compute the deformation gradient/ the Lagrangian Green tensor.
   5. Compute the Cauchy stress or the 2nd P-K stress using the constitutive equation.
   6. Update the nodal internal force ($[\mathbf {f} _{I}^{\text{int}}]$) using $\mathbf {f} _{I}^{\text{int}}=\mathbf {f} _{I}^{\text{int}}+[\mathbf {B} _{I}][{\boldsymbol {\sigma }}]^{T}~J_{\xi }~W_{Q}$ where $W_{Q}$ are the weights for Gaussian integration.

The mass matrix and integration in time will be discussed later.

← Nonlinear elasticity

Nonlinear finite elements

Homework1 →