Nonlinear finite elements/Stress measures

Stress measures

Three stress measures are widely used in continuum mechanics (particularly in the computational context). These are

1. The Cauchy stress (${\boldsymbol {\sigma }}$) or true stress.
2. The Nominal stress (${\boldsymbol {N}}$) (which is the transpose of the first Piola-Kirchhoff stress (${\boldsymbol {P}}={\boldsymbol {N}}^{T}$).
3. The second Piola-Kirchhoff stress or PK2 stress (${\boldsymbol {S}}$).

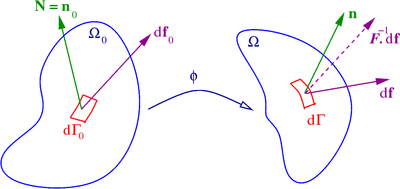
Consider the situation shown the following figure.

Quantities used in the definition of stress measures

The following definitions use the information in the figure. In the reference configuration $\Omega _{0}$, the outward normal to a surface element $d\Gamma _{0}$ is $\mathbf {N} \equiv \mathbf {n} _{0}$ and the traction acting on that surface is $\mathbf {t} _{0}$ leading to a force vector $d\mathbf {f} _{0}$. In the deformed configuration $\Omega$, the surface element changes to $d\Gamma$ with outward normal $\mathbf {n}$ and traction vector $\mathbf {t}$ leading to a force $d\mathbf {f}$. Note that this surface can either be a hypothetical cut inside the body or an actual surface.

Cauchy stress

The Cauchy stress (or true stress) is a measure of the force acting on an element of area in the deformed configuration. This tensor is symmetric and is defined via

$d\mathbf {f} =\mathbf {t} ~d\Gamma ={\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} ~d\Gamma$

or

$\mathbf {t} ={\boldsymbol {\sigma }}^{T}\cdot \mathbf {n}$

where $\mathbf {t}$ is the traction and $\mathbf {n}$ is the normal to the surface on which the traction acts.

Nominal stress/First Piola-Kirchhoff stress

The nominal stress (${\boldsymbol {N}}={\boldsymbol {P}}^{T}$) is the transpose of the first Piola-Kirchhoff stress (PK1 stress) (${\boldsymbol {P}}$) and is defined via

$d\mathbf {f} =\mathbf {t} _{0}~d\Gamma _{0}={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {P}}\cdot \mathbf {n} _{0}~d\Gamma _{0}$

or

$\mathbf {t} _{0}={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {P}}\cdot \mathbf {n} _{0}$

This stress is unsymmetric and is a two point tensor like the deformation gradient. This is because it relates the force in the deformed configuration to an oriented area vector in the reference configuration.

2nd Piola Kirchhoff stress

If we pull back $d\mathbf {f}$ to the reference configuration, we have

$d\mathbf {f} _{0}={\boldsymbol {F}}^{-1}\cdot d\mathbf {f}$

or,

$d\mathbf {f} _{0}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}~d\Gamma _{0}$

The PK2 stress (${\boldsymbol {S}}$) is symmetric and is defined via the relation

$d\mathbf {f} _{0}={\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}~d\Gamma _{0}$

Therefore,

${\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}$

Relations between Cauchy stress and nominal stress

Recall Nanson's formula relating areas in the reference and deformed configurations:

$\mathbf {n} ~d\Gamma =J~{\boldsymbol {F}}^{-T}\cdot \mathbf {n} _{0}~d\Gamma _{0}$

Now,

${\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} ~d\Gamma =d\mathbf {f} ={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}$

Hence,

${\boldsymbol {\sigma }}^{T}\cdot (J~{\boldsymbol {F}}^{-T}\cdot \mathbf {n} _{0}~d\Gamma _{0})={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}$

or,

${\boldsymbol {N}}^{T}=J~({\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }})^{T}=J~{\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}$

or,

${\boldsymbol {N}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\qquad {\text{and}}\qquad {\boldsymbol {N}}^{T}={\boldsymbol {P}}=J~{\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}$

In index notation,

$N_{ij}=J~F_{ik}^{-1}~\sigma _{kj}\qquad {\text{and}}\qquad P_{ij}=J~\sigma _{ik}~F_{jk}^{-1}$

Therefore,

$J~{\boldsymbol {\sigma }}={\boldsymbol {F}}\cdot {\boldsymbol {N}}={\boldsymbol {P}}\cdot {\boldsymbol {F}}^{T}~.$

The quantity ${\boldsymbol {\tau }}=J~{\boldsymbol {\sigma }}$ is called the Kirchhoff stress tensor and is used widely in numerical algorithms in metal plasticity (where there is no change in volume during plastic deformation).

Note that ${\boldsymbol {N}}$ and ${\boldsymbol {P}}$ are not symmetric because ${\boldsymbol {F}}$ is not symmetric.

Relations between nominal stress and second P-K stress

Recall that

${\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}=d\mathbf {f}$

and

$d\mathbf {f} ={\boldsymbol {F}}\cdot d\mathbf {f} _{0}={\boldsymbol {F}}\cdot ({\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0})$

Therefore,

${\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {F}}\cdot {\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}$

or (using the symmetry of ${\boldsymbol {S}}$),

${\boldsymbol {N}}={\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}\qquad {\text{and}}\qquad {\boldsymbol {P}}={\boldsymbol {F}}\cdot {\boldsymbol {S}}$

In index notation,

$N_{ij}=S_{ik}~F_{jk}\qquad {\text{and}}\qquad P_{ij}=F_{ik}~S_{kj}$

Alternatively, we can write

${\boldsymbol {S}}={\boldsymbol {N}}\cdot {\boldsymbol {F}}^{-T}\qquad {\text{and}}\qquad {\boldsymbol {S}}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {P}}$

Relations between Cauchy stress and second P-K stress

Recall that

${\boldsymbol {N}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}$

In terms of the 2nd PK stress, we have

${\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}$

Therefore,

${\boldsymbol {S}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}$

In index notation,

$S_{ij}=F_{ik}^{-1}~\tau _{kl}~F_{jl}^{-1}$

Since the Cauchy stress (and hence the Kirchhoff stress) is symmetric, the 2n PK stress is also symmetric.

Alternatively, we can write

${\boldsymbol {\sigma }}=J^{-1}~{\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}$

or,

${\boldsymbol {\tau }}={\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}~.$

Clearly, from definition of the push-forward and pull-back operations, we have

${\boldsymbol {S}}=\varphi ^{*}[{\boldsymbol {\tau }}]={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}$

and

${\boldsymbol {\tau }}=\varphi _{*}[{\boldsymbol {S}}]={\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}~.$

Therefore, ${\boldsymbol {S}}$ is the pull back of ${\boldsymbol {\tau }}$ by ${\boldsymbol {F}}$ and ${\boldsymbol {\tau }}$ is the push forward of ${\boldsymbol {S}}$.

← Kinematics - objectivity

Nonlinear finite elements

Deviatoric and volumetric stress →