Motion - Kinematics
| Navigation | |
|---|---|
| Next: | Motion - Dynamics |
| Previous: | Motion - Mechanics |
| Up: | Topic: High School Physics |
Kinematics is the branch of mechanics concerned with the motions of objects without being concerned with the forces that cause the motion. In this latter respect it differs from dynamics, which is concerned with the forces that affect motion. There are three basic concepts in kinematics - speed, velocity and acceleration.
Speed
[edit | edit source]The speed of an object is how fast it is moving (the same as the ordinary, everyday definition). Speed in physics is defined as the rate of change of position with no respect to direction.
The standard equation for average speed is
- ,
where
- stands for average speed
- stands for distance = Ending Position - Start Position
- stands for time = Ending time - Beginning time
For example, if a bus takes two hours to travel 100 km, then it has an average speed of
Speed is a scalar value, in comparison to velocity which is a vector
Velocity
[edit | edit source]Velocity is defined as the rate of change of position of a body in a given direction. The velocity of an object (such as a bus) is how fast it is moving in a particular direction. To specify the velocity, both a speed and a direction must be given. Continuing with the bus from the example above, if it is moving east of west, then its velocity is 50 km/h, e of w.
Acceleration
[edit | edit source]Acceleration is the rate of change of velocity. Recalling the definition of velocity, this could mean a change in speed or direction. So, if the bus goes around a curve without slowing down, still traveling at 50 km/hr, but now turning toward the south (say), then it is accelerating, even though its speed isn't changing.
Acceleration will prove to be an important topic when it comes to dynamics, which is concerned with the forces that make objects move.
Uniform motion
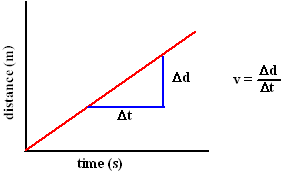
[edit | edit source]The simplest type of motion is where the change in distance is the same for every second; in other words the speed is constant. We call this uniform motion and its distance versus time graph looks like this:
Notice that the speed is the slope of the graph (rise/run). The graph has the same slope (steepness = rise/run) at all times - the speed is constant. When the distance at time zero is zero, the deltas (change in) may be omitted and the formula v = d/t used. This is often written as d = vt. The letter v is commonly used for speed which is the magnitude (size) of velocity.
It is useful to view this another way, as a graph of velocity versus time:

This graph is horizontal because the velocity is constant, the same at all times. Notice that the area under the graph, a rectangle, is vt which is the distance.
We have found relationships among the quantities:
- The slope on the distance versus time graph is the velocity
- The area under the v vs t graph is the distance
The formula only applies to uniform motion, but the graphical relationships turn out to be true for all kinds of motion.
Example 1
[edit | edit source]Sound travels at a velocity of about 340 m/s in air. How far will it go in one tenth of a second?
- Solution
Example 2
[edit | edit source]Light travels at 3.0 x 10^8 m/s. How long will it take to go 10 km?
- Solution
Example 3
[edit | edit source]Three year old Johnny takes off at 2 m/s. Five seconds later, his mom goes after him at 3 m/s. How far does Johnny get before his mother catches him?
- Solution 1
- It looks complicated, so let us picture it with a graph first. On this graph, the red line shows Johnny's motion and the blue line shows Mom's motion.

- You should be able to understand why the red line is drawn where it is - it starts at distance zero at time zero, and its slope must be 2 m/s. Mom's line (blue) starts 5 s later and has a slope of 3. The two meet at approximate time 15 s after Johnny starts, and distance 30 m. Graphical solutions are always approximate.
- Solution 2
Write d = vt for Johnny and again for Mom. We are interested in the time when their distances are equal.
Johnny Mom
d = vt d = vt
2t = 3(t-5) because Mom's running time is 5s less.
2t = 3t - 15 math expansion
0 = 1t - 15 subtract 2t from both sides
15 = t add 15 to both sides
In 15 seconds, Johnny goes 30 m. Mom travels for 10 seconds at 3 m/s so her d = vt = 3x10 = 30 m is the same. The exact answer is 30 meters.
Motion with constant acceleration
[edit | edit source]The next simplest type of motion is where the velocity (speed) is steadily increasing. Velocity is the slope on the distance vs time graph, so the graph must be curved upward. As time increases, the slope or velocity increases.
It is fascinating to see that the area under the velocity graph is equal to the distance in this case, too. We use the math notation A(t) to represent the area under the graph from time zero up to time t. A(t+Δt) is the area up to time t + Δt. The difference between these two areas is the blue shaded area in the diagram above:
A(t+Δt) - A(t) = shaded area = v(t) x Δt
This second equality is not quite right because v(t)xt is only the rectangular area, but the small triangle does not matter as we take Δt to be very small. Mathematicians say, "in the limit as Δt tends to zero."
Dividing both sides by Δt this is
Velocity is the slope or rate of change of distance, and it is the rate of change of the area, so distance and the area under the velocity graph must be the same thing. It is probably more convincing to demonstrate this for yourself with some numerical data for the distance versus time. Any data will do; the relationship turns out to be true for any kind of motion.
Using the idea that distance is the area under the velocity graph, we can now find a formula for distance when the motion is accelerated.
- Example 4
- A falling object accelerates at 9.81 m/s2. A stone is dropped (no initial speed) over a cliff and it takes 2s to fall, how high is the cliff?
- Solution
- Example 5
- If a car accelerates at 2 m/s2, how long will it take to travel 100m?
- Solution
Acceleration is defined as the rate of change of velocity, or the slope on the velocity graph. This gives us or . Usually the motion begins at time zero, so Δt is the same as t, but there is often an initial velocity so . Thus the formula can be written as or most commonly as
- Example 6
- If a car moving at 12 m/s accelerates at 2 m/2 for 10 seconds while passing a truck, how fast will it be going after the 10s?
- Solution
While the formulas are most convenient for most problems, it is worth remembering the graphical relationships, which can be useful for harder problems.
- Example 7
- A bullet moving at 300 m/s hits a wooden block and travels 0.015 m while decelerating in the wood. Assume that the motion is approximately constant accelerated (or decelerated). Calculate the acceleration of the bullet while stopping.