Minkowski diagram

This is on Wikiversity instead of Wikipedia because it contains material that is either unsourced or original. The effort is purely pedagogical, not intended to develop any new theories regarding special relativity. While the Minkowski diagram is probably not a suitable topic for a beginning student in special relativity, the ideas developed here might someday lead to a reassessment of that view. The nice thing about writing for Wikiversity is that we don't need to worry about such issues. This website suggests that these ideas are old (no surprise to me): http://hubpages.com/education/Minkowski-Diagram

See below

Fig. 2

Fig. 3

Fig. 4

Figure 1 explains why superluminal communication violates causality. At time, t=0, Alice will send Bob a message he will receive before she sends it. The train is equipped with a hypothetical instantaneous signal delivery device. Two photons at the center C are sent to the front F and rear R to verify that the message is received the instant it is sent. Alice waits till the front reaches her to send the message that Bob had received a short while ago when the rear of the train passed him. The consequences of a prompt reply (from Bob to Alice) using a similar device is sufficient to convince most that superluminal communication is impossible.

In Figure 2, extra diagonal elements have been added. One is drawn to look like a train, and the other is drawn to mark time an looks like the red 7-segment display of a digital clock. It is convenient if the train is one light-year long (as measured in the the rest frame of Alice and Bob). A time travelSer who "dropped" into an empty seat on the diagonal train might witness the passengers celebrating day when the magic telephone sent the instantaneous message from the front to the back of the train (in their frame it is a simultaneous celebration, but it might not seem so due to look-back effects). A time traveler who "dropped" onto the red digital clock line would be at the center of the train where a one-year clock was marking the time between when two pulses of light were emitted at the center of the train. The endpoints of this digital clock line mark when the pulses were emitted and when they return. Since the train is one light-year long in the reference frame of Alice and Bob, the digital time clock must mark more than one year because the "proper" length of the train is longer than one light-year.

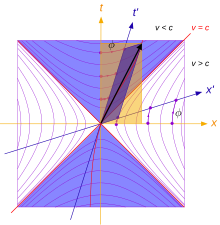
Figure 3 shows a similar diagram with the A train traveling to right, and after rearranging the lines we get Figure 4. Is this related to the Minkowski diagram of Figure 5?

Fig. 5

Draft of letter to AJP or EJP

hide draft for a while

The figure shows how Alice can send Bob a message he received before she sends it. To accomplish this, Alice first hands the message to someone in the front of the train the instant that the train arrives. This train is moving away from Bob and towards Alice, with a speed shown from the figure's slope to be about a third the speed of light. To account for small delays, it might be helpful to imagine a train that is light-years long, and measure time in years so that the speed of light takes the convenient value of 1 light-year/year. The train is moving from Bob towards Alice and is equipped with a hypothetical device that can send an "instantaneous messages", i.e. a signal that moves with infinite speed. Images of moving trains on space-time graphs are complicated by the fact that the orientation of the train depends on the observer's reference frame, so it is best to focus on the paths taken by three points on the train, situated at on paths F, C, and R, representing the train's front, center and rear, respectively. Two light pulses, shown as wavy blue lines, were emitted in opposite directions from the center of the train. This simultaneous emission was timed so that one pulse reaches Alice just as front of the train reaches her, but the purpose of the light pulses is not to send signals, but to mark two simultaneous events in the train's reference frame when both pulses reach the opposite ends of the train. The figure shows that Bob receives the message before it was sent, but the full paradox is achieved when one contemplates a second train moving in the opposite direction also equipped with the hypothetical "instantaneous message" device that would allow the reply to reach Alice several months before the original signal was sent. It is clear that this paradox persists even if one allows for small delays associated with a less idealized system (e.g. if the information speed greatly exceeds the speed of light but is not "instantaneous"). signal delivery device. Two photons at the center C are sent to the front F and rear R to verify that the message is received the instant it is sent. Alice waits till the front reaches her to send the message that Bob had received a short while ago when the rear of the train passed him. The consequences of a prompt reply (from Bob to Alice) using a similar device is sufficient to convince most that superluminal communication is impossible. In Figure 2, extra diagonal elements have been added. One is drawn to look like a train, and the other is drawn to mark time an looks like the red 7-segment display of a digital clock. It is convenient if the train is one light-year long (as measured in the the rest frame of Alice and Bob). A time travelSer who "dropped" into an empty seat on the diagonal train might witness the passengers celebrating day when the magic telephone sent the instantaneous message from the front to the back of the train (in their frame it is a simultaneous celebration, but it might not seem so due to look-back effects). A time traveler who "dropped" onto the red digital clock line would be at the center of the train where a one-year clock was marking the time between when two pulses of light were emitted at the center of the train. The endpoints of this digital clock line mark when the pulses were emitted and when they return. Since the train is one light-year long in the reference frame of Alice and Bob, the digital time clock must mark more than one year because the "proper" length of the train is longer than one light-year. First we consider the simple case of instantaneous communication, i.e., where information travels with infinte speed. The slope of a verticle line is neither positive nor negative. Correspondingly, if a completely rigid rope is pulled, the force or displacement would be translated along the rope in such a way that it would be impossible to ascertain the where the source of this force or displacement is situated. Instantaneous communication is simultaneously transferred to all places along the line of communication. As per convention with such diagrams in special relativity, the x and t axis are reversed from what students usually see. From the slope of the timelines (F, C, R) for the front, center, and rear of the train, we see that the train is moving in the negative direction at a third the speed of light. Alice will send a signal to Bob at t=0, which is exactly when the front of the train reachers her. At some point in the past, two pulses of light (shown as blue wavey arrows) are sent from the center (C) of the train, one directed towards the front (F), and the other towards the rear (R). The two pulses are sent at a time, t<0, which was selected so that the foward directed pulse reaches the front of the train at exactly the same time that the front of the train reaches Alice. Since the two light pulses are sent from the center of the train, their arrival at the front and rear will be simultaneous. The sole purpose of these light pulses is to use their simultaneous arrival at F and R to identify when the signal from Alice to Bob is recieved and sent. The hypothetical "instantaneous message" delivery device is situated on the moving train. The length of the train, as well as the velocity of the two light pulses are all shown as measured in the rest frame of Alice and Bob. The second postulate of special relativity stipulates that is that passengers in the train perceive the pulses to be reaching the front and back parts of the train simultaneously. And it is these moving passengers who observe the hypotheticl "instantaneous message" delivery system in action. Therefore, Bob recieves his message 6 months before Alice sent it, as shown in the figure. However, by the second postulate of e and Bob are one light year apart, and measure time in years. The train in Figure 1 is travelling at a third the speed of light from Bob to Alice, and will The timelines for the front, center, and rear (F,C,R) of the train are shown for a train moving at a third the speed of light. Supposing that a device capable of delivering instantenous signals could be built, we place it on a train traveling at a speed below that of light, in the opposite direction to the desired flow of information. Prior to the front of the train reaching Alice, two light pulses were emitted from the center of the train that travel in opposite directions, timed so that the one pulse reaches Alice at exactly the same time that the other pulse reaches Bob, who is positions so that he is adjacent to the rear of the train at the same time Alice is adjacent to the front. The path taken by these pulses is shown by the the wavy blue lines, and the pulses we created solely in order to establish that the instantaneous signal transmission device is working properly. This diagram is best viewed from the reference frame of Alice and Bob, so that it is the Einstein's second law that ensures that observers on the train also perceive the signals as having equal and opposite speeds, and it is this feature that causes Bob to receive the signal before Alice sent it. To complete the paradox, we need another train travelling in the opposite direction so that Alice can receive her answer well before she sent it. The train is shown moving at a third the speed of light, and the arrow below Alices timeline shows that an instantaneious response by Bob using a similarly moving train would cause his response to arrive approximately 7 months before her question was asked. It is clear that delays in Bob responding and/or superluminal communication that was slightly slower than instantaneious would not remove the paradox.

Trigonometry

Fig. 3

From Figure 3, taking the train's length in to be 1 light-year (in the rest frame of Alice), apply the law of sines to the two triangles at the bottom of the diagram. Then apply the sine sum angle rule to the identities shown in that figure: ${\frac {\sin \delta }{0.5}}={\frac {\sin \epsilon }{b}}$,  and,  ${\frac {\sin \eta }{0.5}}={\frac {\sin \epsilon }{b}}.$

Since tanφ=b/a is the velocity v (if c=1), we have:

  $a={\frac {1}{\sqrt {2}}}{\frac {\cos \phi }{\cos \phi +\sin \phi }}={\frac {1}{\sqrt {2}}}{\frac {1}{1+v}}$

  $b={\frac {1}{\sqrt {2}}}{\frac {\cos \phi }{\cos \phi -\sin \phi }}={\frac {1}{\sqrt {2}}}{\frac {1}{1-v}}$

Instructions for creating you own Minkowski diagram

template

The figure shows how to create a diagram with the train traveling in the negative-x direction.