Materials Science and Engineering/Doctoral review questions/Daily Discussion Topics/01102008
Shift of the Fermi Level
[edit | edit source]
In statistical mechanics, Fermi-Dirac statistics is a particular case of particle statistics developed by Enrico Fermi and Paul Dirac that determines the statistical distribution of fermions over the energy states for a system in thermal equilibrium. In other words, it is a probability of a given energy level to be occupied by a fermion.
More generally, Fermi-Dirac statistics means that the total wavefunction of fermions must be antisymmetric under an exchange of every pair of fermions (that is, if one exchanges any fermion with another, the wavefunction gets an overall minus sign).
Fermions are particles which are [indistinguishable and obey the Pauli exclusion principle, i.e., no more than one particle may occupy the same quantum state at the same time. Fermions have half-integral spin. Statistical thermodynamics is used to describe the behaviour of large numbers of particles. A collection of non-interacting fermions is called a Fermi ga.
F-D statistics was introduced in 1926 by Enrico Fermi and Paul Dirac and applied in 1926 by Ralph Fowler to describe the collapse of a star to a white dwarf and in 1927 by Arnold Sommerfeld to electrons in metals. Pascual Jordan developed in 1925 the same statistics which he called Pauli statistics. The problem was that his referee Max Born forgot the paper for six months before finding it again. In the meantime it was independently discovered by Enrico Fermi and Paul Dirac.
For F-D statistics, the expected number of particles in states with energy is
where:
- is the number of particles in state i,
- is the energy of state i,
- is the degeneracy of state(density of states) i (the number of states with energy ),
- is the chemical potential (Sometimes the Fermi energy is used instead, as a low-temperature approximation),
- is Boltzmann's constant, and
- is absolute temperature.
In the case where is the Fermi energy and , the function is called the Fermi function:
At temperatures above 1000 K, the Fermi level decreases
Bloch Theorem
[edit | edit source]A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle (usually, an electron) placed in a periodic potential. It consists of the product of a plane wave envelope function and a periodic function (periodic Bloch function) which has the same periodicity as the potential:
The result that the eigenfunctions can be written in this form for a periodic system is called Bloch's theorem. The corresponding energy eigenvalue is Єn(k)= Єn(k + K), periodic with periodicity K of a reciprocal lattice vector. Because the energies associated with the index n vary continuously with wavevector k we speak of an energy band with band index n. Because the eigenvalues for given n are periodic in k, all distinct values of Єn(k) occur for k-values within the first Brillouin zone of the reciprocal lattice.
Periodic Potential and Expression with Fourier Series
[edit | edit source]
- : Translation vector of the lattice
- : sum over all reciprocal vectors
- : Fourier coefficients of the potential
- : Reciprocal lattice vector
Expression of Wave Function with Fourier Transformation
[edit | edit source]
- : Fourier coefficients of the wave function
- : Wave vectors
k vectors
[edit | edit source]
- : magnitude of reciprocal lattice vector
- : whole set of reciprocal lattice vectors
- : intersperse points between reciprocal lattice points
Connection between wave vectors and reciprocal vectors
[edit | edit source]Express any wave vector, , as the sum of a reciprocal vector, , and wave vector that is within the Brillouin zone.
- : wavevector always confined to the Brillouin zone of the reciproval lattice
Substitute expressions into the Schrodinger equation
[edit | edit source]
Rename the summation indices and replace
The equation is true with regard to an space vector
The known Fourier coefficients of the periodic potential are coupled to the Fourier coefficients of the wave function.
Splitting of Atomic Orbitals
[edit | edit source]Atomic Orbitals
[edit | edit source]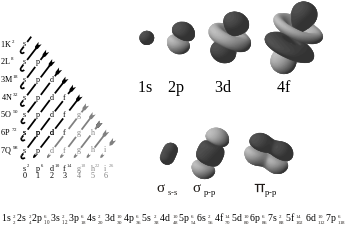
Timeline of Development
[edit | edit source]The developments of the atomic orbital model proceeded along the following timeline:
5th century BC: The ancient Greek philosophers Leucippus and his pupil Democritus proposed that all matter was composed of small indivisible particles called atoms.
1800-1810: Dalton examined the empirical compositions of chemical compounds and proposed a set of rules regarding the properties of the elements and how they combined to form compounds, leading to the Billard Ball theory.
1897: J. J. Thompson published his work on the discovery of the electron. This led to the plum pudding model of the atom.
1905: Albert Einstein demonstrated the photo-electric effect which showed that the frequency of light was proportional to the energy. This discovery would later be used to relate emission and absorption spectra to the electron structure of atoms, leading to the equation E=MC2
1909: Ernest Rutherford led scattering experiments on gold foils (gold-foil experiment), and thereby discovered the nucleus
1911: Rutherford proposed the Rutherford model based on the earlier experimental work in which a cloud of electrons orbit the nucleus.
1913: Niels Bohr proposed the Planetary Model of the atom.
1925: Erwin Schrodinger proposed the Schrödinger equation, which allowed the electrons in an atom to be analyzed quantum mechanically (Quantum Mechanics). This led to the current atomic orbital model of the atom, the Quantum Mechanic model or the Electron Cloud model
A Mathematical Function
[edit | edit source]
An atomic orbital is a mathematical function that describes the wave-like behavior of an electron in an atom. The region in which an electron may be found around a single atom in a particular energy state can be calculated from this function. The term "orbital" has become known as either the "mathematical function" or the "region" generated with the function. Specifically, atomic orbitals are the possible quantum states of an individual electron in the electron cloud around a single atom, as described by the function.
Classically, the electrons were thought to orbit the atomic nucleus, much like the planets around the Sun (or more accurately, a moth orbiting very quickly around a lamp). Explaining the behavior of the electrons that "orbit" an atom was one of the driving forces behind the development of quantum mechanics. In quantum mechanics, atomic orbitals are described as wave functions over space, indexed by the n, l, and m quantum numbers of the orbital or by the names as used in electron configurations, as shown on the right. As electrons cannot be described as solid particles (as a planet or a moth) in this way, a more accurate analogy would be that of a huge atmosphere, the spatially distributed electron, around a tiny planet which is the atomic nucleus. Hence the term "orbit" was substituted with something else: orbital.
The orbital names (s, p, d, f, g, h,...) are derived from the characteristics of their spectroscopic lines: sharp, principal, diffuse and fundamental, the rest being named in alphabetical order.
Chemical Bonding
[edit | edit source]
A chemical bond is the physical process responsible for the attractive interactions between atoms and molecules, and that which confers stability to diatomic and polyatomic chemical compounds. The explanation of the attractive forces is a complex area that is described by the laws of quantum electrodynamics. In practice, however, chemists usually rely on quantum theory or qualitative descriptions that are less rigorous but more easily explained to describe chemical bonding. In general, strong chemical bonding is associated with the sharing or transfer of electrons between the participating atoms. Molecules, crystals, and diatomic gases—indeed most of the physical environment around us—are held together by chemical bonds, which dictate the structure of matter.
Molecular Orbitals
[edit | edit source]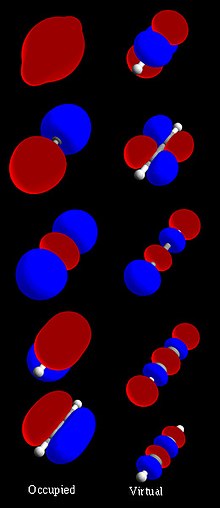
A molecular orbital specifies the spatial distribution and energy of one (or one pair of) electron(s). Most commonly a MO is represented as a linear combination of atomic orbitals (the LCAO-MO method), especially in qualitative or very approximate usage. They are invaluable in providing a simple model of bonding in molecules.
Most methods in computational chemistry today start by calculating the MOs of the system. A molecular orbital describes the behavior of one electron in the electric field generated by the nuclei and some average distribution of the other electrons. In the case of two electrons occupying the same orbital, the Pauli principle demands that they have opposite spin. Necessarily this is an approximation, and highly accurate descriptions of the molecular electronic wave function do not have orbitals (see configuration interaction).
HOMO/LUMO
[edit | edit source]When the molecule forms a dimer or an aggregate, the proximity of the orbitals of the different molecules induce a splitting of the HOMO and LUMO energy levels. This splitting produces vibrational sublevels which each have their own energy, slightly different from one another. There are as many vibrational sublevels as there are molecules that interact together. When there are enough molecules influencing each other (e.g. in an aggregate), there are so many sublevels that we no longer perceive their discrete nature: they form a continuum. We no longer consider energy levels, but energy bands.
Argon
[edit | edit source]
Argon’s complete octet of electrons indicates full s and p subshells. This full outer energy level makes argon very stable and extremely resistant to bonding with other elements. Before 1962, argon and the other noble gases were considered to be chemically inert and unable to form compounds; however, compounds of the heavier noble gases have since been synthesized. In August 2000, the first argon compounds were formed by researchers at the University of Helsinki. By shining ultraviolet light onto frozen argon containing a small amount of hydrogen fluoride, argon hydrofluoride (HArF) was formed. It is stable up to 40 kelvins (−233 °C).
Although the neutral ground-state chemical compounds of argon are presently limited to HArF, argon can form clathrates with water when atoms of it are trapped in a lattice of the water molecules. Also argon-containing ions e.g. ArH+ and excited state complexes e.g. ArF are well known. Theoretical calculations on computers have shown several argon compounds that should be stable but for which no synthesis routes are currently known.
Brillouin Zone
[edit | edit source]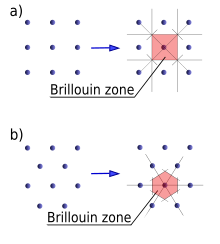
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell of the reciprocal lattice in the frequency domain. It is found by the same method as for the Wigner-Seitz cell in the Bravais lattice. The importance of the Brillouin zone stems from the Bloch wave description of waves in a periodic medium, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone.
Taking the surfaces at the same distance from one element of the lattice and its neighbours, the volume included is the first Brillouin zone. Another definition is as the set of points in k-space that can be reached from the origin without crossing any Bragg plane.
There are also second, third, etc., Brillouin zones, corresponding to a sequence of disjoint regions (all with the same volume) at increasing distances from the origin, but these are used more rarely. As a result, the first Brillouin zone is often called simply the Brillouin zone. (In general, the n-th Brillouin zone consist of the set of points that can be reached from the origin by crossing n − 1 Bragg planes.)
Critical Points
[edit | edit source]
Several points of high symmetry are of special interest – these are called critical points.
| Symbol | Description |
|---|---|
| Γ | Center of the Brillouin zone |
| Simple cube | |
| M | Center of an edge |
| R | Corner point |
| X | Center of a face |
| Face-centered cubic | |
| K | Middle of an edge joining two hexagonal faces |
| L | Center of a hexagonal face |
| U | Middle of an edge joining a hexagonal and a square face |
| W | Corner point |
| X | Center of a square face |
| Body-centered cubic | |
| H | Corner point joining four edges |
| N | Center of a face |
| P | Corner point joining three edges |
| Hexagonal | |
| A | Center of a hexagonal face |
| H | Corner point |
| K | Middle of an edge joining two rectangular faces |
| L | Middle of an edge joining a hexagonal and a rectangular face |
| M | Center of a rectangular face |





















![{\displaystyle \Psi (r)=\sum _{k}C_{k}\exp[ikr]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1d669e29fbf6df60f2f0f8e84a7dfbcf55f2c3)











![{\displaystyle \left[{\frac {-\hbar ^{2}\nabla ^{2}}{2m}}+V({\overrightarrow {r}})\right]\Psi =E\Psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/29eecfed8e88e4494e4019951102406839dc8a8a)
![{\displaystyle \sum _{k}{\frac {(\hbar k)^{2}}{2m}}C_{k}\exp(ikr)+\sum _{k'}\sum _{G}C_{k'}V_{G}\exp(i[k'+G]\cdot r=E\sum _{k}C_{k}\exp(ikr)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac15189ce779fdcd898e69fa8d62770303d5f338)




![{\displaystyle \sum _{k}e^{ikr}\left[\left({\frac {\hbar ^{2}k^{2}}{2m}}-E\right)C_{k}+\sum _{G}V_{G}C_{k-G}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96c46160216a2bb7fd55cd58916d5504be336254)


