Mandelbrot set as a model for the concept of approximation

This short article by Dan Polansky presents the idea that computer plots of Mandelbrot set provide an interesting, highly visual and intuitive model for the concept of approximation. The thing modeled or illustrated is a process producing successively better representations of the underlying reality. But the thing approximated does not need to be reality; it can be a desired system of rules of action.

The concept of ever improving approximation is well illustrated e.g. by calculations of decimal expansions of the number of pi, or even of 1/3. However, this does not provide any visual, intuitive look; the thing approximated is one-dimensional. In the Mandelbrot set, a certain two-dimensional geometric figure is approximated, first very crudely as a circle, then as an oval, etc., then with increasing detail. Compared to e.g. Sierpinsky triangle, the Mandelbrot set appears much less predictable in a sense. The Sierpinsky triangle is exactly self-similar and increasing revelation of detail provides no surprise. By contrast, the Mandelbrot set seems to reveal ever new shapes and structures. The newly revealed detail of the Mandelbrot set is not a mere recursive extrapolation of the detail already revealed by cruder approximations. Another two-dimensional approximation is a series of photographs with increasing image resolution, the number of pixels. The approximative process of the Mandelbrot set is rather different: each approximation can be thought of as a mathematically smooth set (of transfinitely many points/complex numbers) that merely happens to be pixelated. Thus, an n-approximation is the set of all complex values c such than the quadratic map iteration started from 0 does not escape the 0-centered circle with the radius of 2 in n iteration steps.

In the following image series, the Mandelbrot set approximation is the dark area. One can see how structural elements of the underlying shape emerge and increase in number. The series is missing the circle as an initial step and starts with an oval instead, the next step after circle. One could even consider the zeroth approximation to be the full plane: the initial 0 cannot escape the 2-circle in zero iteration steps. Such zeroth approximation shows zero power of differentiation; by contrast, the circle differentiates points that have no chance to be in the set from points that, on extremely low effort, appear to have a chance to be in the set.

• 
• 
• 
• 
• 

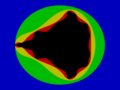
The following image shows the boundaries of the successive approximations.

A related concept illustrated is that of plausibility checking. The ever better approximations correspond to someone running ever more expensive plausibility checks on the hypothesis that, given the parameter c, the system starting from zero does not escape to infinity. Someone very lazy or short of computational resources can only run, say, 2 iterations and still rule out a large area of values.

Above, we showed what might be termed approximation from above. However, we may also show approximation from below, of the Mandelbrot set. We may note that the main cardioid appears to be in the Mandelbrot set, as well as series of disks attached to the cardioid or to other disks. To this, we may add the anthena going to the point -2 + 0i and the cardioids (and their disks) located on that anthena. This concept is illustrated in the following image, except that no attempt is made to include the main antenna and other antennas:

That's it for today. Hope you learned or realized something interesting.

Further reading

• Mandelbrot set, wikipedia.org
• Approximation, wikipedia.org