Correlation

Completion status: this resource is ~50% complete.

Correlation (co-relation) refers to the degree of relationship (or dependency) between two variables.

Linear correlation refers to straight-line relationships between two variables.

A correlation can range between -1 (perfect negative relationship) and +1 (perfect positive relationship), with 0 indicating no straight-line relationship.

The earliest known use of correlation was in the late 19th century[1].

Introduction

The degree of linear relationship between two variables can be represented in terms of a Venn Diagram. Perfectly overlapping circles would indicate a correlation of 1, and non-overlapping circles would represent a correlation of 0.

When we ask questions such as "Is X related to Y?", "Does X predict Y?", and "Does X account for Y"?, we are interested in measuring and better understanding the relationship between two variables.

Correlation measures the extent to which variables:

covary
depend on one another
predict one another

The extent of correlation between two variables, by convention, is denoted r, and the correlation between variable X and variable Y is indicated by r_XY.

Correlations are standardised to vary between -1 and +1, with 0 representing no relationship, -1 a perfect negative relationship, and +1 a perfect positive relationship.

A variety of bivariate correlational statistics are available, the choice of which depends on the variables' level of measurement:

Nominal by nominal: Contingency table, Pearson's chi-square test, Phi/Cramer's V
Ordinal by ordinal: Spearman's rho, Kendall's tau-b
Dichotomous by interval/ratio: Point biserial correlation coefficient
Interval/ration by interval/ratio: Pearson product-moment correlation coefficient

Correlational analyses should be accompanied by appropriate bivariate graphs, such as:

Nominal by nominal: Clustered bar charts
Ordinal by ordinal: Scatterplot (with point bins)
Interval/ratio by interval/ratio: Scatterplot

The world is made of covariation

Responses which vary can be measured as a variable (i.e., responses are distributed across a range).

Responses to two or more variables may covary. These variables share some variation. When the value of one variable is high, the value of other variable tends to be high (positive correlation) or low (negative correlation).

If you look around, you may notice that the world is made of covariation! e.g.,

pollen count is positively correlated with bee activity
rainfall is positively correlated with amount of vegetation
hours of study is positively correlated with test performance
number of fire trucks attending a fire is correlated with cost of repairs for the fire[2]
Sibling's IQ is positively correlated
perceived air temperature is negatively correlated with amount of clothing worn

The more you look, the more you'll see that there are many predictable patterns of co-occurrence between phenomena (i.e., things tend to occur together).

Scatterplots

Independent variable (IV) (predictor) is placed on the X axis and dependent variable (DV) is placed on the Y axis. Each case is plotted according to its X and Y value.

Visual inspection of scatterplots is essential

It is unwise to rely solely on correlation as a statistic that indicates the nature of the relationship between variables without also examining a visualisation of the data such as through a scatterplot.

For example, the linear (straight-line) correlation in each of these four scatterplots is .82, yet the nature of what the data indicated about the relationship between the variables is very different for each.

Homoscedasticity

If the data are normally distributed, then scatterplots should be homoscedastistic (even spread about the line of best fit).

If data are not normally distributed (e.g., skewed), then the bivariate distribution may be heteroscedastic (uneven spread about the line of best fit). This violate the assumption of homoscedasticity for correlation.

For more information, see Homoscedasticity and Heteroscedasticity (Wikipedia).

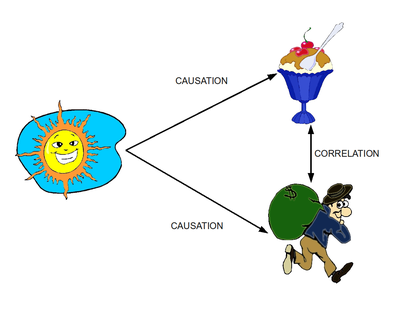
Correlation does not equal causation

Correlation does not prove causation, although it may be consistent with causation. It is important to understand that correlation does not equal causation. A relationship between two variables may be caused by a third variable.

See Correlation does imply causation (Wikipedia)

Range restriction

For more info, see the effect of range restrictions (Howell, 2009) and restricted range (Lane, n. d.).

For a practical tutorial, see outliers and restricted range.

Coefficient of determination

When a correlation coefficient (r) is squared (r²), this gives the coefficient of determination which is the percentage of variance shared between the two variables.

See also

Lecture slide
References
- Allen & Bennett, 2010, p. 173
- Howell, 2010, p. 344
Coefficient of determination (Wikipedia)

Interactive activity

Correlation guess: Correlation guess

Quiz

Test yourself: This is a pre-quiz to see what you already know - Introductory quiz

External links

11 ways to look at the chi-squared coefficient for contingency tables
13 ways to look at the correlation coefficient
Correlation (Annis, 2008)
Correlation (Garson, 2008)
Correlation (Plonsky, 2006)
Correlation (Trochim, 2006)
Correlation coefficient (Hopkins, 2000)
Correlation coefficients (Calkins, 2005)
New poll shows correlation is causation (Humour)
Rank order correlation (Lowry, 2008)
Tutorial - Correlation (Neill, 2010)
Understanding correlation (Rummel, 1976)