Kirchhoff's Voltage Law

From Wikiversity

Wikiversity Electrical Engineering School
The Lessons in
ELECTRIC CIRCUITS ANALYSIS COURSE

Circuit Analysis Part II (Laws & Theorems)

This part is an introduction to some useful Electric Circuit Laws and theorems. You are encouraged to master the theorems and laws that will be discussed herein as they form a basis upon which most Circuit analysis methods are built.

Lesson Review

What you need to remember from Previous Lessons.

Review all lessons thus far ( i,e Read and be sure you understand lesson reviews done thus far )

Lesson 5: Preview

This Lesson is about Kirchhoff's Voltage Law. The student/User is expected to understand the following at the end of the lesson.

Remember what was learned in Passive sign convention, You can go back and revise Lesson 1.

Define Kirchhoff's Voltage Law ( word-by-word ).

Kirchhoff's Voltage Law:

∑ v_n = v₄ + v₁ + v₂ + v₃ = 0

n

Lessons in Electric Circuit Analysis

Lesson #1:

Passive sign convention

Lesson #2:

Simple Resistive Circuits

Lesson #3:

Resistors in Series

Lesson #4:

Resistors in Parallel

Quiz Test:

Circuit Analysis Quiz 1

Lesson #5:

Kirchhoff's Voltage Law

Lesson #6:

Kirchhoff's Current Law

Lesson #7:

Nodal analysis

Lesson #8:

Mesh Analysis

Quiz Test:

Circuit Analysis Quiz 2

Home Laboratory:

Circuit Analysis - Lab1

Part 1: Kirchhoff's Voltage Law

Kirchhoff's Voltage Law states:

The sum of the voltages around a closed circuit path must be zero.

Notice that a closed circuit path insists that if one circuit element is chosen as a starting point, then one must be able to traverse the circuit elements in that loop and return to the element in the beginning.

Mathematically, The Kirchhoff's Voltage Law is given by

∑	v_n = 0
n

For reference, this law is sometimes called Kirchhoff's Second Law, Kirchhoff's Loop Rule, and Kirchhoff's Second Rule.

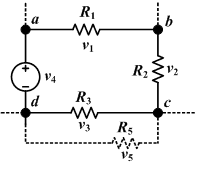
Part 2:Kirchhoff's Voltage Law (Cont...)

Figure 5.1: $v 4 + v 1 + v 2 + v 3 = 0$

We observe five voltages in Figure 5.1:
v₄ across a voltage source, and the four voltages v₁, v₂, v₃ and v₅ across the resistors R₁, R₂, R₃ and R₅, respectively.
The voltage source and resistors R₁, R₂ and R₃ comprise a closed circuit path, thus the sum of the voltages v₄, v₁, v₂ and v₃ must be zero:

∑	v_n = v₄ + v₁ + v₂ + v₃ = 0
n

The resistor R₅ is outside the closed path in question, and thus plays no role in the calculation of Kirchhoff's Voltage Law for this path. (Note that alternate closed paths can be defined which include the resistor R₅. In these cases, the voltage v₅ across R₅ must be considered in calculating Kirchhoff's Voltage Law.)

Part 3

Now, if we take the point d in the image as our reference point and arbitrarily set its voltage to zero, we can observe how the voltage changes as we traverse the circuit clockwise.

Going from point d to point a across the voltage source, we experience a voltage increase of v₄ volts (as the symbol for the voltage source in the image indicates that point a is at a positive voltage with respect to point d).

On traveling from point a to point b, we cross a resistor. We see clearly from the diagram that, since there is only a single voltage source, current must flow from it's positive terminal to its negative terminal--clockwise around the circuit path. Thus from Ohm's Law, we observe that the voltage drops from point a to point b across resistor R₁.

Likewise, the voltage drops across resistors R₂ and R₃. Having crossed R₂ and R₃, we arrive back at point d, where our voltage is zero (just as we defined). So we experienced one increase in voltage and three decreases in voltages as we traversed the circuit.

The implication from Kirchhoff's Voltage Law is that, in a simple circuit with only one voltage source and any number of resistors, the voltage drop across the resistors is equal to the voltage applied by the voltage source:

v 4 = v 1 + v 2 + v 3

Kirchhoff's Voltage Law can easily be extended to circuitry that contains capacitors.

Part 4 : Example

Figure 5.2: Example 1

Consider Figure 5.2 with the following Parameters:

V 1 = 15 V

V 2 = 7 V

R 1 = 20Ω

R 2 = 5Ω

R 3 = 10Ω

Find current through $R 3$ using Kirchhoff's Voltage Law.

Solution:

Figure 5.3: Example 1 loops

We can see that there are two closed paths (loops) where we can apply KVL in, Loop 1 and 2 as shown in figure 5.3

From Loop 1 we get:

V 1 - V R 3 - V R 1 = 0

From Loop 2 we get:

V 2 - V R 3 - V R 2 = 0

A bit confused? well look at the explanation in Part 3 of this lesson and Review Passive sign convention.

Part 5 : Example (Continued)

The above results can further be simplified as follows:

$V 1 - (I 1 - I 2) * R 3 - I 1 * R 1 = 0$

$I_2 = \frac{I_1\times{(R_3+R_1)} - V_1}{R_3}$ ..... (1)

and

$V 2 + (I 1 - I 2) * R 3 - I 2 * R 2 = 0$

$I_2 = \frac{I_1\times{R_3} + V_2}{R_2 + R_3}$ ..... (2)

By equating above (1) and (2) we can eliminate $I 2$ and hence get the following:

$I_1 = \frac{V_2*R_3 + V_1*(R_2+R_3)}{(R_2+R_3)(R_3+R_1)-R_{3}^{2}}$ ..... (3)

We end up with the above three equations and now substitute the Values given in the above equations and solve the variables.

If you feel lost up to this point do go back to the beginning of the example. Think of this as just another mathematical problem requiring solving by use of simultaneous equations with two unknowns!

Notice that we work with Variables only and try to solve the equation to its simplest form. Only after we have arrived at a simplified equation then that we can substitute in values of Resistors, Voltages and current. This can save you a lot of trouble because, if you go wrong you can easily trace your work to the problem.

Part 6 : Example (Continued)

It is clear that: from (3)

$\begin{matrix}\ I_1 &=& \frac{(7V)*(10\Omega) + (15V)*(15\Omega)}{(15\Omega)*(30\Omega)-(10\Omega)^{2}} \\ \ \\ \ &=& \frac{295}{350} \\ \ \\ \ & = & 0.843A \end{matrix}$ .

Substitute the Above Result into (2)

$\begin{matrix}\ I_2 &=& \frac{(7V)+(0.843A\times{10\Omega})}{15\Omega} \\ \ \\ \ &=& \frac{15.43V}{15\Omega} \\ \ \\ \ & = & 1.029A \end{matrix}$ .

The Positive sign for $I 2$ only tells us that Current $I 2$ flows in the same direction to our initial assumed direction. Thus now we can calculate Current through $R 3$ as follows:
$\begin{matrix}\ I_{R3} &=& (I_1 - I_2) \\ \ \\ \ &=& 0.843A -(1.029A) \\ \ \\ \ & = & -0.186A \end{matrix}$ .

The Negative sign for $I R 3$ only tells us that Current $I R 3$ flows in the same direction to $I 2$ direction.

If you are lost repeat this example and try to follow the logic, otherwise just send a message to the course instructor as outlined in Part 8.

Part 7:

The method used to solve the above problem is very tedious, when the complexity of the circuit is increased the method becomes very cumbersome and almost impossible to use in solving circuit equations. This method is used just to illustrate KVL in this lesson. In Lesson 08 a more efficient method of solving these kinds of Circuit problems using KVL is introduced in a form of Mesh Analysis.

Try the following exercise on your own and compare your answers with the given possible solution.

Exercise 5

Figure 5.4: Exercise 5

Consider Figure 5.4 with the following Parameters:

V 1 = 15 V

V 2 = 7 V

R 1 = 20Ω

R 2 = 5Ω

R 3 = 10Ω

Find current through $R 3$ using Kirchhoff's Voltage Law.

Answers to Exercise 5

Part 8:

Further Reading Links:

Kirchhoff's circuit laws

References:

Nilsson, James W. and Riedel, Susan A. Electric Circuits (5th ed.). Addison-Wesley. (1996).ISBN 020155707X

Completion list

Once you finish your Exercises you can post your score here! To post your score just e-mail your course co-ordinator your name and score *Click Here .