Jet engine performance notes
Engine Sizing
[edit | edit source]Civil Engines
[edit | edit source]Modern (i.e. high bypass ratio) civil engines are normally sized to meet the the thrust requirements at the Top-of-Climb, which is often the design condition for the engine.
The throttle setting used at Take-Off depends upon the aircraft configuration: i.e. whether it has two, three or four-engines fitted. In the Western World, civil engines operate to a "set and forget" throttle setting throughout Take-off. If the thrust of one engine is lost during the Take Off, the remaining engine/s must have sufficient total thrust to allow the aircraft to clear any immediate obstruction beyond the end of the runway (e.g. buildings).
So if one engine is lost on a twin engine aircraft (e.g. Boeing 777) during Take-off, the remaining 50% of thrust must be sufficient to meet the above criteria. Consequently the implied nominal T/O thrust must be very high, which results in the aircraft having a very steep climb-out from the airport.
On the other hand, if one engine is lost during Take-off on a four engined aircraft (e.g. Boeing 747), there is still 75% of the nominal total thrust to meet the above criteria. So the implied nominal T/O thrust can be relatively low, resulting in the aircraft having a shallower climb-out.
Military Engines
[edit | edit source]The sizing point for a military engine is very much dependent upon the aircraft application.
As example, the Pegasus engine fitted in the Harrier is sized to meet the thrust requirements for a vertical landing in a hot climate, with a high level of reaction control bleed from the HP compressor. These severe requirements mean there is more than sufficient thrust for normal wing-borne operation and so, in-flight, the engine is significantly derated (i.e. throttled back).
Husk plot
[edit | edit source]A Husk Plot is a concise way of summarizing the performance of a jet engine. The following sections describe how the plot is generated and can be used.
Thrust/SFC loops
[edit | edit source]Specific Fuel Consumption (i.e. SFC), defined as fuel flow/net thrust, is an important parameter reflecting the overall thermal (or fuel) efficiency of an engine.
As an engine is throttled back there will be a variation of SFC with net thrust, because of changes in the engine cycle (e.g. lower overall pressure ratio) and variations in component performance (e.g. compressor efficiency). When plotted, the resultant curve is known as a thrust/SFC loop. A family of these curves can be generated at Sea Level, Standard Day, conditions over a range of flight speeds. A Husk Plot (RHS) can be developed using this family of curves. The net thrust scale is simply relabeled , where is relative ambient pressure , whilst the SFC scale is relabeled , where is relative ambient temperature. The resulting plot can be used to estimate engine net thrust and SFC at any altitude, flight speed and climate for a range of throttle setting.

Selecting a point on the plot, net thrust is calculated as follows:
Clearly, net thrust falls with altitude, because of the decrease in ambient pressure.
The corresponding SFC is calculated as follows:
At a given point on the Husk Plot, SFC falls with decreasing ambient temperature (e.g. increasing altitude or colder climate).The basic reason why SFC increases with flight speed is the implied increase in ram drag.
Although a Husk Plot is a concise way of summarizing the performance of a jet engine, the predictions obtained at altitude will be slightly optimistic. For instance, because ambient temperature remains constant above 11,000 m (36,089 ft) altitude, at a fixed non-dimensional point the Husk plot would yield no change in SFC with increasing altitude. In reality, there would be a small, steady, increase in SFC, owing to the falling Reynolds number.
Thrust lapse
[edit | edit source]The nominal net thrust quoted for a jet engine usually refers to the Sea Level Static (SLS) condition, either for the International Standard Atmosphere (ISA) or a hot day condition (e.g. ISA+10 °C). As an example, the GE90-76B has a take-off static thrust of 76,000 lbf (360 kN) at SLS, ISA+15 °C.
Naturally, net thrust will decrease with altitude, because of the lower air density. There is also, however, a flight speed effect.
Initially as the aircraft gains speed down the runway, there will be little increase in nozzle pressure and temperature, because the ram rise in the intake is very small. There will also be little change in mass flow. Consequently, nozzle gross thrust initially only increases marginally with flight speed. However, being an air breathing engine (unlike a conventional rocket) there is a penalty for taking on-board air from the atmosphere. This is known as ram drag. Although the penalty is zero at static conditions, it rapidly increases with flight speed causing the net thrust to be eroded.
As flight speed builds up after take-off, the ram rise in the intake starts to have a significant effect upon nozzle pressure/temperature and intake airflow, causing nozzle gross thrust to climb more rapidly. This term now starts to offset the still increasing ram drag, eventually causing net thrust to start to increase. In some engines, the net thrust at say Mach 1.0, sea level can even be slightly greater than the static thrust. Above Mach 1.0, with a subsonic inlet design, shock losses tend to decrease net thrust, however a suitably designed supersonic inlet can give a lower reduction in intake pressure recovery, allowing net thrust to continue to climb in the supersonic regime.
The thrust lapse described above depends on the design specific thrust and, to a certain extent, on how the engine is rated with intake temperature. Three possible ways of rating an engine are depicted on the above Husk Plot. The engine could be rated at constant turbine entry temperature, shown on the plot as . Alternatively, a constant mechanical shaft speed could be assumed, depicted as . A further alternative is a constant compressor corrected speed, shown as . The variation of net thrust with flight Mach number can be clearly seen on the Husk Plot.
Other trends
[edit | edit source]The Husk Plot can also be used to indicate trends in the following parameters:
1) turbine entry temperature
So as ambient temperature falls (through increasing altitude or a cooler climate), turbine entry temperature must also fall to stay at the same non-dimensional point on the Husk Plot. All the other non-dimensional groups (e.g. corrected flow, axial and peripheral Mach numbers, pressure ratios, efficiencies, etc will also stay constant).
2) mechanical shaft speed
Again as ambient temperature falls (through increasing altitude or a cooler climate), mechanical shaft speed must also decrease to remain at the same non-dimemsional point.
By definition, compressor corrected speed, , must remain constant at a given non-dimensional point.
Rated Performance
[edit | edit source]Civil
[edit | edit source]
Nowadays, civil engines are usually flat-rated on net thrust up to a 'kink-point' climate. So at a given flight condition, net thrust is held approximately constant over a very wide range of ambient temperature, by increasing (HP) turbine rotor inlet temperature (RIT or SOT). However, beyond the kink-point, SOT is held constant and net thrust starts to fall for further increases in ambient temperature. Consequently, aircraft fuel load and/or payload must be decreased.
Usually, for a given rating, the kink-point SOT is held constant, regardless of altitude or flight speed.
Some engines have a special rating, known as the 'Denver Bump'. This invokes a higher RIT than normal, to enable fully laden aircraft to Take-off safely from Denver, CO in the summer months. Denver Airport is extremely hot in the summer and the runways are over a mile above sea level. Both of these factors affect engine thrust.
Military
[edit | edit source]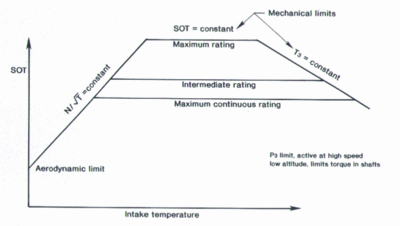
The rating systems used on military engines vary from engine to engine. A typical military rating structure is shown on the left. Such a rating system maximises the thrust available from the engine cycle chosen, whilst respecting the aerodynamic and mechanical limits imposed on the turbomachinery. If there is adequate thrust to meet the aircraft's mission in a particular range of intake temperature, the engine designer may elect to truncate the schedule shown, to lower the turbine rotor inlet temperature and, thereby, improve engine life.
At low intake temperatures, the engine tends to operate at maximum corrected speed or corrected flow. As intake temperature rises, a limit on (HP) turbine rotor inlet temperature (SOT) takes effect, progressively reducing corrected flow. At even higher intake temperatures, a limit on compressor delivery temperature (T3) is invoked, which decreases both SOT and corrected flow.
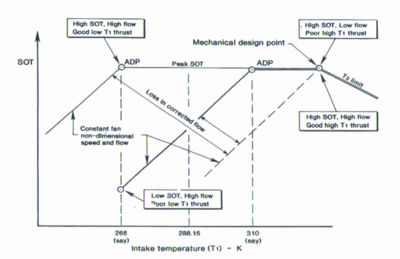
The impact of design intake temperature is shown on the right hand side.
An engine with a low design T1 combines high corrected flow with high rotor turbine temperature (SOT), maximizing net thrust at low T1 conditions (e.g. Mach 0.9, 30000 ft, ISA). However, although turbine rotor inlet temperature stays constant as T1 increases, there is a steady decrease in corrected flow, resulting in poor net thrust at high T1 conditions (e.g. Mach 0.9, sea level, ISA).
Although an engine with a high design T1 has a high corrected flow at low T1 conditions, the SOT is low, resulting in a poor net thrust. Only at high T1 conditions is there the combination of a high corrected flow and a high SOT, to give good thrust characteristics.
A compromise between these two extremes would be to design for a medium intake temperature (say 290 K).
As T1 increases along the SOT plateau, the engines will throttle back, causing both a decrease in corrected airflow and overall pressure ratio. As shown, the chart implies a common T3 limit for both the low and high design T1 cycles. Roughly speaking, the T3 limit will correspond to a common overall pressure ratio at the T3 breakpoint. Although both cycles will increase throttle setting as T1 decreases, the low design T1 cycle has a greater 'spool-up' before hitting the corrected speed limit. Consequently, the low design T1 cycle has a higher design overall pressure ratio.
Nomenclature
[edit | edit source]- flow area
- calculated nozzle effective throat area
- design point nozzle effective throat area
- nozzle geometric throat area
- shaft angular acceleration
- arbitrary lines which dissect the corrected speed lines on a compressor characteristic
- specific heat at constant pressure for air
- specific heat at constant pressure for combustion products
- calculated nozzle discharge coefficient
- thrust coefficient
- ambient pressure/Sea Level ambient pressure
- turbine enthalpy drop/inlet temperature
- change in mechanical shaft speed
- excess shaft power
- excess shaft torque
- compressor polytropic efficiency
- turbine polytropic efficiency
- acceleration of gravity
- gross thrust
- net thrust
- ram drag
- ratio of specific heats for air
- ratio of specific heats for combustion products
- spool inertia
- mechanical equivalent of heat
- constant
- constant
- constant
- flight Mach number
- compressor mechanical shaft speed
- compressor corrected shaft speed
- turbine corrected shaft speed
- static pressure
- stagnation (or total) pressure
- compressor pressure ratio
- intake pressure recovery factor
- gas constant
- density
- specific fuel consumption
- stator outlet temperature
- (turbine) rotor inlet temperature
- static temperature or time
- stagnation (or total) temperature
- intake stagnation temperature
- compressor delivery total temperature
- ambient temperature/Sea Level, Standard Day, ambient temperature
- total temperature/Sea Level, Standard Day, ambient temperature
- velocity
- mass flow
- calculated turbine entry corrected flow
- compressor corrected inlet flow
- design point turbine entry corrected flow
- corrected entry flow from turbine characteristic (or map)
- combustor fuel flow
Notes
[edit | edit source]References
[edit | edit source]- Kerrebrock, Jack L. (1992), Aircraft Engines and Gas Turbines, The MIT Press, Cambridge, Massachusetts USA. ISBN 0 262 11162 4































































